Demystifying DC Machines: Exploring Different Types and Applications

Except the above, there are also permanent magnet type DC generators. In these generators, no field winding is placed around the poles.

These machines have fairly constant magnetic field. Although these machines are very compact but are used only in small sizes like dynamos in automobiles etc.

The main disadvantages of these machine is that the flux produced by the magnets deteriorates with the passage of time which changes the characteristics of the machine.

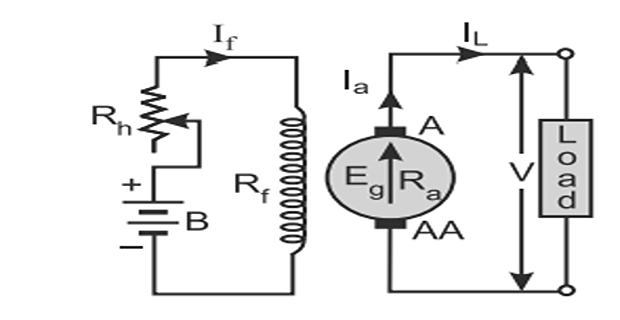
A DC generator in which current is supplied to the field winding from an external DC source is called a separately excited DC generator.

The flux produced by the poles depends upon the field current with in the unsaturated region of magnetic material of the poles (i.e.,$\phi\propto I_{f}$, but in the saturated region, the flux remains constant.

$I_{a}$ = $I_{L}$

Terminal voltage, V=$E_{g}-$$I_{a}$$R_{a}$

If contact brush drop per brush ($v_{b}$) is known, $V=E_{g}-I_{a}$$R_{a}-2v_{b}$

Power developed =$E_{g}$$I_{a}$

Power output = $VI_{L}$=$V$$I_{a}$

In a shunt wound generator, the field winding is connected across the armature winding forming a parallel or shunt circuit

Full terminal voltage is applied across the field winding.

A very small current $I_{sh}$ flows through it because this winding has many turns of fine wire having very high resistance $R_{sh}$ (of the order of 100 ohm).

Shunt field current, $I_{sh}$=V/$R_{sh}$

• $R_{sh}$ is the shunt field winding resistance.

• $I_{sh}$ is practically constant at all loads

• therefore, the DC shunt machine is considered to be constant flux machine.

Armature current, $I_{a}=I_{L}+I_{sh}$

Terminal voltage, V =$E_{g}-IR_{a}$

Including brush contact drop, V =$E_{g}-IR_{a}$$-2v_{b}$

Power developed = $E_{g}$$I_{a}$

Power output =$VI_{L}$

Field winding is connected in series with the armature winding forming a series circuit.

Full line current $I_{L}$ or armature current $I_{a}$ flows through it.

Since the series field winding carries $I_{F.L}$, it has a few turns of thick wire having low resistance (usually of the order of less than one ohm).

Series field current, $I_{se}$=$I_{L}$=$I_{a}$

Series field winding resistance =$R_{se}$

Terminal voltage, V =$E_{g}-I_{a}$$R_{a}$$-I_{se}$$R_{se}$=$E_{g}$-$I_{a}(R_{a}+R_{se})$

Including brush contact drop, V =$E_{g}$-$I_{a}(R_{a}+R_{se})$-2$v_{b}$

Power developed = $E_{g}$$I_{a}$

Power output = $VI_{L}=VI_{a}$

Note: The flux developed by the series field winding is directly proportional to the current flowing through it $\phi\propto I_{se}$. But it is only true before magnetic saturation, after saturation flux becomes constant even if the current flowing through it is increased.

There are two sets of field windings on each pole.

One of them is connected in series (having few turns of thick wire) and the other is connected in parallel (having many turns of fine wire) with armature.

A compound wound generator may be;

• Long-shunt

• Short-shunt

Long shunt in which the shunt field winding is connected in parallel with the combination of both armature and series field winding.

Shunt field current, $I_{sh}=\frac{V}{R_{sh}}$

Series field current, $I_{se}$=$I_{a}=I_{L}+I_{sh}$

Terminal voltage, $V=E_{g}-I_{a}$$R_{a}$-$I_{se}$-$R_{se}$$=E_{g}-I_{a}($$R_{a}$+$R_{se})$

Including brush contact drop, V$=E_{g}-I_{a}($$R_{a}$+$R_{se})$-2$v_{b}$

Power developed =$E_{g}$$I_{a}$

Power output = V$I_{L}$

Short shunt in which the shunt field winding is connected in parallel with only armature winding.

Series field current, $I_{se}$=$I_{L}$

Shunt field current, $I_{sh}=\dfrac{V+I_{L}}{R_{sh}}$$R_{se}$=$\dfrac{E_{g}-I_{a}}{R_{sh}}$$R_{a}$ $I_{a}=I_{L}+I_{sh}$

Terminal voltage, V =$E_{g}-I_{a}$$R_{a}$-$I_{L}$$R_{se}$

Including brush contact drop, V =$E_{g}-I_{a}$$R_{a}$-$I_{L}$$R_{se}$-2$v_{b}$

Power developed =$E_{g}$$I_{a}$

Power output = V$I_{L}$

In compound wound DC generators, the field is produced by the shunt as well as series winding.

Generally the shunt field is stronger than the series field.

When the series field assist the shunt field, the generator is called as cumulatively compound wound generator.

However, when the series field opposes the shunt field, the generator is known as differentially compound wound generator.