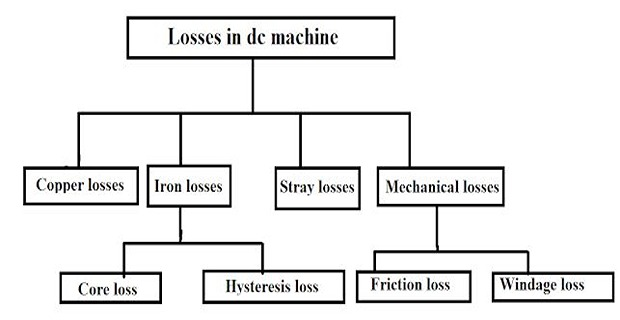
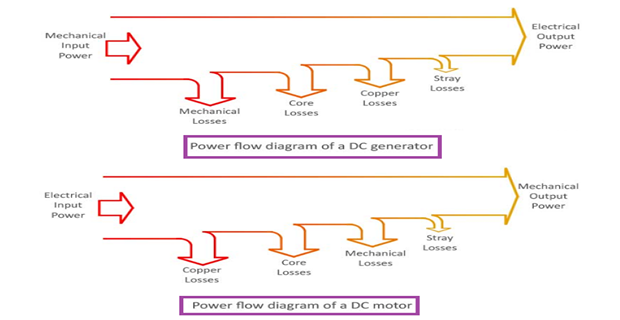
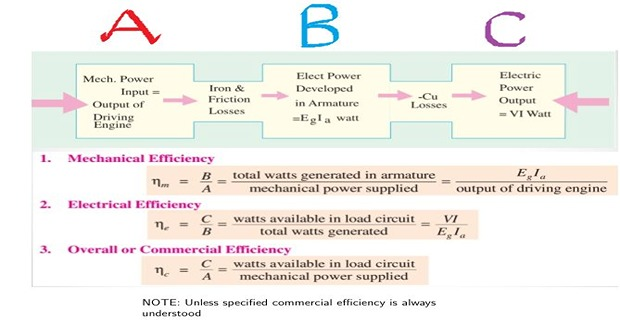
Copper Losses:
Generally occurs due to current in the various windings:
\[\left.\begin{array}{ll}\mathrm{Armature~copper~loss}=I_{a}^{2}R_{a}\cdots3-6\%\\\mathrm{Shunt~field~copper~loss}&=I_{sh}^{2}R_{sh}\\\mathrm{Series~field~copper~loss}&=I_{se}^{2}R_{se}\end{array}\right\}\mathrm{1-5\%}\]
Additionally loss due to brush contact resistance enclosed in
armature copper loss
Iron Losses:
Loss within the armature due its rotation within the magnetic field
of the poles.
\[\text{Hysteresis loss}=K_hB_{max}^{1.6}fV\\\text{Eddy Current loss}=K_eB_{max}^2f^2V\]
Mechanical (Rotational) Losses
3-15%
Friction: in bearings, brushes, etc.
Windage: air friction of rotating coil
Losses rely on the speed of the machine.
Stray Losses:
1% of FL Output Power
Miscellaneous losses occurs due to
Distortion of flux because of armature reaction
Short circuit currents in the coil, undergoing
commutation
Very difficult to determine a reasonable value is assigned
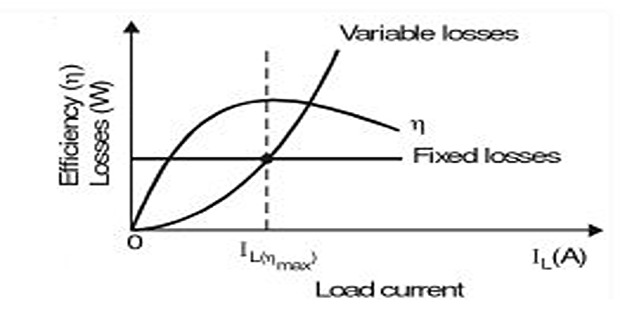
Constant Losses:
Iron losses
Mechanical losses
Shunt field losses
Variable Losses:
\[\boxed{\mathrm{Total~losses}=\mathrm{Constant~Losses~+~Variable~Losses}}\]
\[\begin{aligned}
\dfrac{d}{dI}\left(\dfrac{IR_{a}}{V}+\dfrac{W_{c}}{VI}\right) & =
0\\
\dfrac{R_a}{V} - \dfrac{W_c}{VI^2} & = 0\\
I^2R_a & = W_c
\end{aligned}\]
\[\begin{aligned}
I^2R_a & = W_c\\
&\boxed{I = \sqrt{\dfrac{W_c}{R_a}}}
\end{aligned}\]
\[\boxed{\mbox{Variable loss = constant
loss}}\]
Now, efficiency is maximum when denominator is minimum i.e. when