Transformer Testing: OC & SC Tests Unveiled

Demonstrative Video

SINGLE PHASE TRANSFORMER

OBJECTIVE

To determine the parameters of the equivalent circuit of a single phase transformer and predetermine the performance characteristics, by performing the OC and SC test on single phase transformer

NAME PLATE DETAILS OF SINGLE PHASE TRANSFORMER
KVA Rating	2 KVA
HV Volts	230 VAC
LV Volts	115 VAC
HV current	8.6 A
LV current	17.3 A
Winding type	Core

APPARATUS REQUIRED:

S.No.	Name of the Equipment	Range	Quantity	Type
1.	Single Phase Verica	0 to 230V/15 A	1 No	Core
2.	Voltmeter	0 to 150 V	1 No	Digital
3.	Voltmeter	0 to 50 V	1 No	Digital
4.	Ammeter	5 A	1 No	Digital
5.	Ammeter	10 A	1 No	Digital
6.	Wattmeter ( LPF )	150/300V/10A	1 No	Digital
7.	Wattmeter ( UPF )	75/150/20A	1 No	Digital

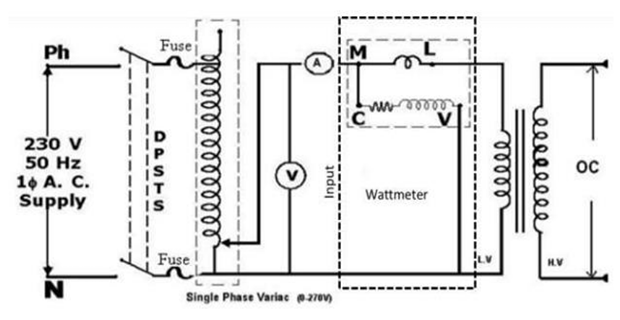
CIRCUIT DIAGRAM FOR OPEN CIRCUIT TEST:

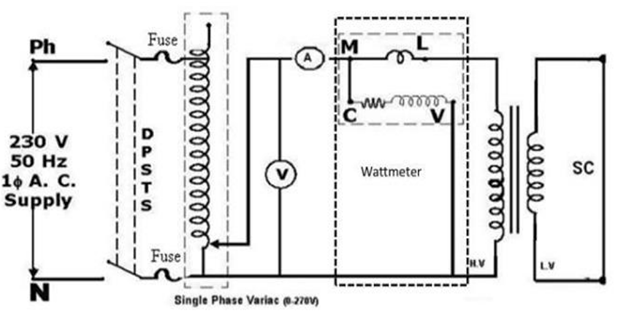
CIRCUIT DIAGRAM FOR SHORT CIRCUIT TEST:

INTRODUCTION:

A transformer is a static device comprising of two coils coupled through a magnetic medium connecting two ports at different (sometime same) voltage levels in an electric system allowing the interchange of electrical energy in either direction via magnetic field. The schematic diagram of a transformer is shown in Figure.

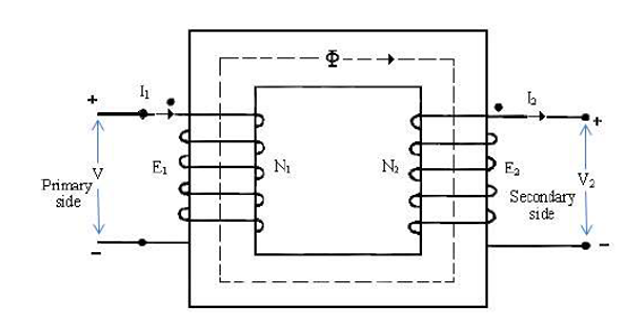
An ideal transformer obeys the following relations:

\begin{matrix} \frac{E_{1}}{E_{2}} & = \frac{V_{1}}{V_{2}} = \frac{N_{1}}{N_{2}} \frac{I_{1}}{I_{2}} & = \frac{N_{2}}{N_{1}} \end{matrix}

$\begin{aligned} \dfrac{E_1}{E_2}&=\dfrac{V_1}{V_2}=\dfrac{N_1}{N_2}\\ \dfrac{I_1}{I_2}&=\dfrac{N_2}{N_1} \end{aligned}$

Impedance seen on primary (impedance-transformation property)

$\begin{aligned} Z_2^{\prime}&=Z_2\cdot \left(\dfrac{N_1}{N_2}\right)^{2} \end{aligned}$

THEORY:

Transformer is a device that transfers electrical energy from one circuit to another by electromagnetic induction (transformer action).
The electrical energy is always transferred without a change in frequency, but may involve changes in magnitudes of voltage and current.
Because a transformer works on the principle of electromagnetic induction, it must be used with an input source voltage that varies in amplitude.

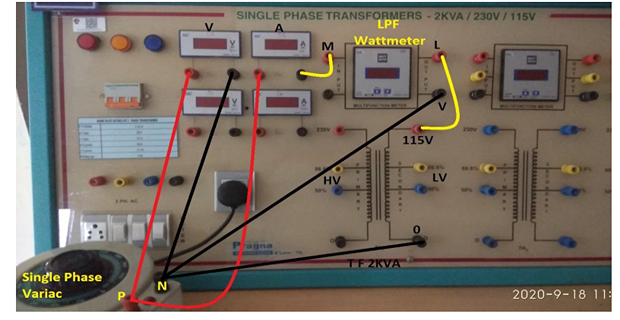
EM LAB SET-UP:

CONNECTION FOR O.C TEST:

Single Phase Verica Positive (R) to Ammeter (R)
Single Phase Verica (R) to Voltmeter (R)
Ammeter (B) to Wattmeter M (LPF)
Wattmeter L to LV Side T/F 115V(R)
Single Phase Verica Negative (B) to Voltmeter (B)
Single Phase Verica Negative (B) to Wattmeter V
Single Phase Verica Negative (B) to LV Side T/F 0 (B)
HV Side is Open

PROCEDURE FOR O.C TEST:

Connect the circuit for no-load test as per the circuit diagram.
Keep the variac in minimum position and switch ON the 1-ɸ AC supply.
Apply the rated voltage to the LV side of the transformer by properly adjusting the variac.
Note down the readings of various meters such as Ammeter, Voltmeter & Wattmeter.
After taking the readings, put the variac to minimum position & Switch OFF the 1-ɸ AC supply

OBSERVATION TABLE FOR O.C TEST:

S.No.

V_oc(V)

I_oc(A)

W_oc= W× M.F.(w)

CONNECTION FOR S.C TEST:

Single Phase Verica Positive (R) to Ammeter (R)
Single Phase Verica (R) to Voltmeter (R)
Ammeter (B) to Wattmeter M (UPF)
Wattmeter L to HV Side T/F 230V(R)
Single Phase Verica Negative (B) to Voltmeter (B)
Single Phase Verica Negative (B) to Wattmeter V
Single Phase Verica Negative (B) to HV Side T/F 0 (B)
LV Side is Short

PROCEDURE FOR S.C TEST:

Connect the circuit for SC test as per the circuit diagram, with appropriate range of meters.
Keep the variac in minimum position and switch ON the 1-ɸ AC supply.
Apply appropriate voltage (low voltage) to the transformer by adjusting the variac such that rated current flows through the transformer.
Note down the readings of various meters such as Ammeter, Voltmeter & Wattmeter.
After taking the readings, put the variac to minimum position and switch off the 1-ɸ AC supply.

OBSERVATION TABLE FOR S.C TEST:

S.No.

V_sc(V)

I_sc(A)

W_sc= W× M.F.(w)

where,

M. F. = Multiplication factor = $(VI\cos\phi)/\mathrm{FSD}$ FSD = Full scale divisions

CALCULATION:

FORMULAS:

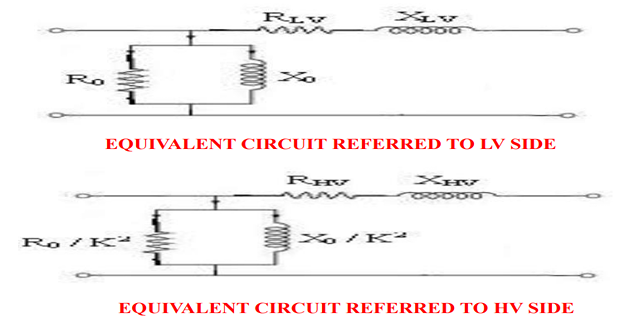
By the equivalent circuit parameters $R_0, X_0, R_{01}, R_{02}, X_{01}$ and $X_{02}$ are found from the O.C. and S.C. test results, draw the equivalent circuit referred to L.V. side as well as H.V. side.

Primary is L.V. side:

$\phi_0 = \cos^{-1} \left( \frac{W_0}{V_0 I_0} \right)$

$R_0 = \frac{V_0}{I_W}$ where

$I_W = I_0 \cos \phi_0$

$X_0 = \frac{V_0}{I_m}$ where

$I_m = I_0 \sin \phi_0$

Secondary is H.V. side:

$R_{HV} = \frac{W_{sc}}{I_{sc}^2}$ ,

$Z_{HV} = \frac{V_{sc}}{I_{sc}}$ ,

$X_{HV} = \sqrt{Z_{HV}^2 - R_{HV}^2}$

$X_{LV} = K^2 X_{HV}$ ,

$R_{LV} = K^2 R_{HV}$

Where

$K = \frac{V_2}{V_1}$ = Transformation ratio.

METER DESIGNING:

Rated current on LV side: (Transformer KVA / LV rated Voltage)

Rated current on HV side: (Transformer KVA / HV rated Voltage)

EQUIVALENT CIRCUIT OF TRANSFORMER:

With transformer parameter values obtained OC and SC tests, fill in the values in the equivalent circuits

CALCULATIONS OF EFFICIENCY & REGULATION:

At ½ full load

Copper losses = $W_{SC} \times \left( \frac{1}{2} \right)^2$ watts, where $W_{SC}$ = full load copper losses
Constant losses = $W_0$ watts
Output = ½ KVA x $\cos \phi$ ( $\cos \phi$ may be assumed)
Input = Output + Copper Loss + Constant loss

$\%$ Efficiency =

$\frac{\text{Output}}{\text{Input}} \times 100$

$\%$ Regulation =

$\frac{I_2(R_{LV} \cos \theta \pm X_{LV} \sin \theta)}{V_2} \times 100$

‘ + ‘ sign for Lagging power factor and ‘ - ‘ sign for Leading power factor

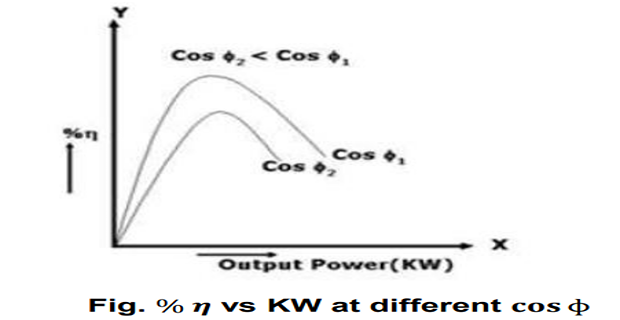
EFFICIENCY Vs LOAD CHARACTERISTICS:

At 0.8 Pf lag

Output P₀ = K × (Rated KVA) × (0.80)

Iron loss (Constant loss) = P_i = W₀

Copper loss = K² P_C = K² W_sc

Where W_sc at rated current = copper loss at rated = I_rated² × R_equ

Total loss = P_L = (P_i + K² P_C)

Input power (P_input) = P₀ + P_L = K × (rated KVA) × (0.8) + P_i + K² P_C

Efficiency = η = output / input

TABULATION:

S.No	1	2	3	4	5	6	7	8
Different Transformer Loading (K)	0.15	0.30	0.45	0.60	0.75	0.90	1.05	1.20
Copper Losses (K²P_C)
Iron Losses (P_i) / Constant Losses
Total loss = P_L = (P_i + K²P_C)
Output Power (P₀) in KW

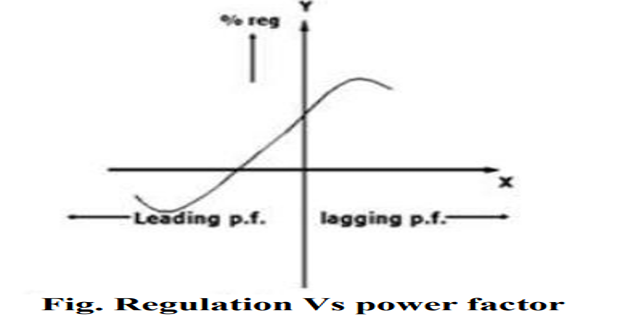
REGULATION Vs POWER FACTOR:

Determine the following either on LV or HV side

Rated voltage V = R=

Rated current I = X =

Power Factor	1.0	0.8	0.6	0.4	0.2
R cos ɸ
X sin ɸ
R cos ɸ + X sin ɸ
R cos ɸ - X sin ɸ
Regulation (LAG)
Regulation (LEAD)

Mark the power factor corresponding to zero voltage regulation.

MODEL GRAPHS:

GRAPHS:

Plots should be drawn between

% efficiency Vs output
% regulation Vs power factor

DATA PROCESSING:

- $Y_0 = \frac{I_0}{V_0}$

- $G_i = \frac{W_0}{(V_0)^2}$

- $B_m = \sqrt{Y_0^2 - G_i^2}$

- $Z_{eq} = \frac{V_{sc}}{I_{sc}}$

- $R_{eq} = \frac{W_{sc}}{(I_{sc})^2}$

- $X_{equ} = \sqrt{Z_{eq}^2 - R_{eq}^2}$

DRAW THE EQUIVALENT CIRCUIT:

Draw the Equivalent circuit referred to the LV side & HV side.

RESULT & QUESTIONS:

RESULT:

Equivalent circuit parameters referred to low voltage side and high voltage side.

LOAD	EFFICIENCY
1/4
1/2
3/4
FULL

PF at which regulation is zero =

QUESTIONS:

What are the losses of transformers?
Why an LPF wattmeter is required in OC test?
Can the regulation become zero? If so, under what conditions ?
What are the advantages of performing the OC and SC test on transformer?