Unsymmetrical Faults Solved Problems

Demonstrative Video

Revision of important Concepts

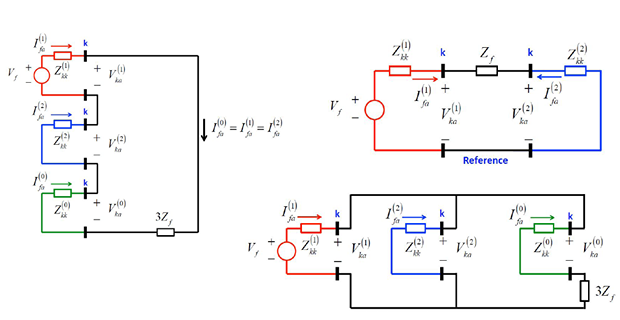
Problem-1

A 25 MVA, 13.2 kV alternator with solidly grounded neutral has a sub-transient reactance of 0.25 pu. The negative and zero sequence reactance are 0.35 and 0.1 pu, respectively. A single line to ground fault occurs at the terminals of an unloaded alternator. Neglecting resistance, determine

the fault current and the line-to-line voltages.

Solution-1

Let the line-to-neutral voltage at the fault point before the fault be \(1.0+j0.00\) p.u.
For LG-fault, the \(Z_f\) is \(j0.25+j0.35+j0.1=j0.7\)

\[\begin{aligned} I_{a1}& = \dfrac{E_a}{Z_1+Z_2+Z_0}\\ &= \dfrac{1}{j0.7} = -j1.428 \end{aligned}\]

\[I_{a1} = I_{a2} = I_{a0} = -j1.428\]
For a L-G fault:
\[\begin{aligned} I_a & = I_{a1} + I_{a2} + I_{a0} \\ & = 3I_{a1} = -j4.285 \end{aligned}\]
The p.u. fault current
Let base be 25 MVA and 13.2 kV
\(I_b=\dfrac{25 \times 1000}{\sqrt{3} \times 13.2} = 1093~A\)
The actual fault current = \(1093 \times 4.285=4685~A\)

\[\begin{aligned} V_{a1} & = E_a - I_{a1}\cdot Z_1\\ & = 1-(-j1.428)(j0.25)\\ & = 0.643\\ V_{a2} & = -I_{a2}Z_2 = -(-j1.128)(j0.35)\\ & = -0.4998\\ V_{a0} & = -I_{a0}Z_0\\ &= - (-j1.428)(j0.1)=0.1428 \end{aligned}\]
To find out the voltages, first compute sequence components of voltages
As a numeric check \(V_a = V_{a1}+V_{a2} + V_{a0} =0\)
\(V_{b}=V_{b1}+V_{b2}+V_{b0}\) and \(V_{c}=V_{c1}+V_{c2}+V_{c0}\)

\[\begin{aligned} V_{b1}=& \lambda^{2} V_{a_{1}}\\ &=(-0.5-j 0.866)(0.643) \\ &=-0.3215-j 0.5568 \\ V_{b2}=& \lambda V_{a_{2}}\\ &=(-0.5+j 0.866)(-0.50) \\ &=(0.25-j 0.433) \\ V_{b0} &=V_{a_{0}}=V_{c_{0}}=-0.1428 \end{aligned}\]

\[\begin{aligned} V_{b} &=-0.3215-j 0.5568+0.25-j 0.433-0.1428 \\ &=-0.2143-j 0.9898 \\ V_{c} &=-0.3215+j 0.5568+0.25+j 0.433-0.1428 \\ &=-0.2143+j 0.9898 \end{aligned}\]

\[\begin{aligned} V_{a b} &=V_{a}-V_{b} . \text { since } V_{a}=0 \\ V_{a b} &=-V_{b}=0.2143+j 0.9898 \\ V_{a c} &=-V_{c}=0.2143-j 0.9898 \\ V_{b c} &=V_{b}-V_{c}=-j 2 \times 0.9898 \\ &=-j 1.9796 \end{aligned}\]
Now, Line-to-Line voltage are:
\[\begin{aligned} V_{a b} &=0.2143+j 0.9898 \\ |V_{a b}|&=1.0127 \mathrm{p} \cdot \mathrm{u} \end{aligned}\]
Now
\[\begin{array}{l} V_{a b}=1.0127 \times \frac{13.2}{\sqrt{3}}=7.717 \mathrm{kV} \\ V_{a c}=7.717 \mathrm{kV} \\ V_{b c}=1.9796 \times \frac{13.2}{\sqrt{3}}=15.08 \mathrm{kV} \end{array}\]
The Line-to-Line voltage will be

Problem-2

Determine the fault current and the line-to-line voltage at the fault when a line-to-line fault occurs at the terminals of the alternator described in the Previous question.

Solution-2

\[\begin{aligned} I_{a_{1}} &=\frac{E_{a}}{Z_{1}+Z_{2}}=\frac{1+j 0.0}{j 0.25+j 0.35} \\ &=\frac{1+j 0.0}{j 0.6}=-j 1.667 \end{aligned}\]

\[\begin{array}{l} I_{a_{1}}=-I_{a_{2}}=-j 1.667 \\ I_{a_{2}}=j 1.667 \\ I_{a_{0}}=0 \end{array}\]
For LL fault
\[\begin{aligned} I_{b} &=I_{b_{1}}+I_{b_{2}}+I_{b_{0}}=I_{b_{1}}+I_{b_{2}}=\lambda^{2} I_{a_{1}}+\lambda I_{a_{2}} \\ &=(-0.5-j 0.866)(-j 1.667)+(-0.5+j 0.866)(j 1.667) \\ &=j 0.833-1.4436-j 0.833-1.4436 \\ &=-2.8872 \mathrm{p} \cdot \mathrm{u} \end{aligned}\]
, use To find out the fault current,

we know \(I_b=1093~A\)
Fault current \(=1093 \times 2.8872=3155.71\) amperes
\[\begin{aligned} V_{a_{1}} &=E_{a}-I_{a_{1}} Z_{1}=1+j 0.0-(-j 1.667)(j 0.25) \\ &=1-0.4167=0.5833 \\ V_{a_{2}} &=-I_{a_{2}} Z_{2}=(-j 1.667)(j 0.35)=0.5834 \\ V_{a_{1}} &=V_{a_{2}}=0.5833 \mathrm{p} \cdot \mathrm{u} \\ V_{a} &=V_{a_{1}}+V_{a_{2}}+V_{a_{0}}=V_{a_{1}}+V_{a_{2}}=2 \times 0.5833=1.1666 \mathrm{p} . \mathrm{u} . \\ V_{b} &=\lambda^{2} V_{a_{1}}+\lambda V_{a_{2}} \\ &=(-0.5-j 0.866)(0.5833)+(-0.5+j 0.866)(0.5833) \\ &=-0.5833 \\ V_{b} &=V_{c}=-0.5833 \end{aligned}\]
To find out L-L voltage, find sequence voltages:

\[\begin{array}{l} V_{a b}=V_{a}-V_{b}=1.1666-(-0.5833)=1.7499 \\ V_{a c}=V_{a}-V_{c}=1.7499 \\ V_{b c}=V_{b}-V_{c}=0.0 \end{array}\]
Line voltages
\[\begin{array}{l} V_{a b}=1.7499 \times \frac{13.2}{\sqrt{3}}=13.33 \mathrm{kV} \\ V_{a c}=13.33 \mathrm{kV} \\ V_{b c}=0.0 \mathrm{kV} \end{array}\]
L-L voltages

Problem-3

Determine the fault current and the line-to-line voltages at the fault when a double line-to-ground fault occurs at the terminals of the alternator described in the previous question

Solution-3

\[\begin{aligned} I_{a_{1}} &=\frac{E_{a}}{Z_{1}+\frac{Z_{0} Z_{2}}{Z_{0}+Z_{2}}}=\frac{1+j 0.0}{j 0.25+\frac{j 0.1 \times j 0.35}{j 0.45}}=\frac{1+j 0.0}{j 0.25+j 0.0778} \\ &=\frac{1+j 0.0}{j 0.3278}=-j 3.0506 \mathrm{p.u} \end{aligned}\]
Compute
\[\begin{array}{l} V_{a_{1}}=V_{a_{2}}=V_{a_{0}} \\ V_{a_{1}}=E_{a}-I_{a_{1}} Z_{1} \end{array}\]
For LLG fault
To find out \(I_{a2}\) and \(I_{a0},\) we should first find \(V_{a1}\)
Since \(V_{a_{1}}=V_{a_{2}}=-I_{a_{2}} Z_{2}, I_{a_{2}}\) can be obtained.
Similarly, \(V_{a_{1}}=V_{a_{0}}=-I_{a_{0}} Z_{0}, I_{a_{0}}\) can be obtained.

\[\begin{aligned} V_{a_{1}} &=1+j 0.0-(-j 3.0506)(j 0.25) \\ &=1-0.7626=0.2374 \\ V_{a_{2}} &=V_{a_{0}}=0.2374 \\ I_{a_{2}} &=-\frac{V_{a_{2}}}{Z_{2}}=-\frac{0.2374}{j 0.35}=j \frac{0.2374}{0.35}=j 0.678 \\ I_{a_{0}} &=-\frac{V_{a_{0}}}{Z_{0}}=-\frac{0.2374}{j 0.1}=j 2.374\\ I_{a_{2}}+I_{a_{0}}&=j 0.678+j 2.374=j 3.05=-I_{a_{1}} \end{aligned}\]

Fault current \(=I_{b}+I_{c}=3 I_{a_{0}}=3 \times j 2.374=j 7.122 \mathrm{p} . \mathrm{u} .\)
\[1093 \times 7.122=7784.3 \text { amperes }\]
Since base current is 1093 amperes, the fault current will be
\[\begin{array}{l} V_{a}=V_{a_{1}}+V_{a_{2}}+V_{a_{0}}=3 V_{a_{1}}=3 \times 0.2374=0.7122 \\ V_{b}=V_{c}=0 \end{array}\]
Now,

\[\begin{aligned} V_{a b} &=V_{a}=0.7122 \times \frac{13.2}{\sqrt{3}}=5.42 \mathrm{kV} \\ V_{a c} &=V_{a}=0.7122 \times \frac{13.2}{\sqrt{3}}=5.42 \mathrm{kV} \\ V_{b c} &=0.0 \mathrm{kV} \end{aligned}\]

The line-to-line fault voltage,