Transmission Line Capacitance Calculation

Demonstrative Video

Problem-1

Calculate the capacitance of phase to neutral per km of a \(3\phi\) line having conductor of 2 cm diameter placed at the corners of a triangle with sides of lengths 5m, 6m, 7m respectively. Assume that the line is fully transposed and carries only balanced load.

Solution-1

Diameter = 2 cm
GMR = Radius = 1 cm = 0.01 m
GMD = \(\sqrt[3]{5\times6\times7}= 5.9439\) m
\[\begin{aligned} C_n & = \dfrac{2\pi\epsilon}{ln\left(\dfrac{GMD}{GMR}\right)} \\ & = \dfrac{2\pi\times 8.85\times 10^{-12}}{ln\left(\dfrac{5.9439}{0.01}\right)}\\ & = 8.7\times 10^{-12}~\text{F/m} \end{aligned}\]
Capacitance (Line to neutral)

Problem-2

What is the capacitance of neutral/km of a single phase line composed of number 2 single strand conductor radius 0.328 cm, spaced 3 m apart and 7.5 m above the ground ? (with and without the earth effect)

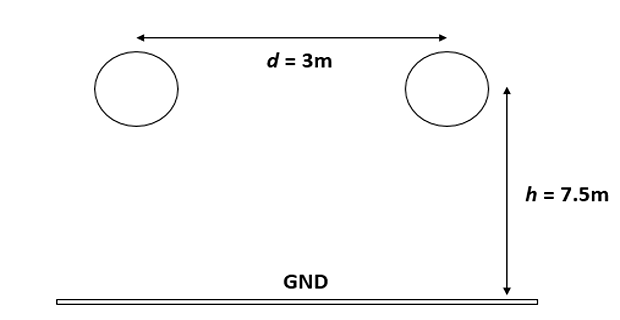
Solution-2

\[\begin{aligned} \mathrm{Cn} &=\frac{2 \pi \epsilon}{\ln \left(\frac{D}{r}\right)} \mathrm{F} / \mathrm{m} \\ &=\frac{2 \pi \times 8.854 \times 10^{-12}}{\ln \left(\frac{3}{0.328 \times 10^{-2}}\right)} \\ &=8.17 \times 10^{-12} \mathrm{F} / \mathrm{m} \\ &=0.00817 \mu \mathrm{F} / \mathrm{km} \end{aligned}\]
Without Earth effect,

\[\begin{aligned} \mathrm{Cn}&=\frac{2 \pi \epsilon}{\ln \left(\frac{D}{r} \times \frac{2 h}{\sqrt{D^{2}+(2 h)^{2}}}\right)} \mathrm{F} / \mathrm{m} \\ & =\dfrac{2\pi\times8.854\times10^{-12}}{\ln\left(\dfrac{3}{0.328\times10^{-2}}\times\dfrac{2\times7.5}{\sqrt{3^{2}+\left(2\times7.5\right)^{2}}}\right)}\\ & =8.1782\times10^{-12}~\mathrm{F} / \mathrm{m} \end{aligned}\]
with Earth effect (Single-phase line),

Problem-3

Calculate the 50 Hz susceptance to neutral per kilometre of a double circuit three phase line with transposition as shown in the fig. given each conductor is 7 m apart and radius of each conductor is 1.38 cm.

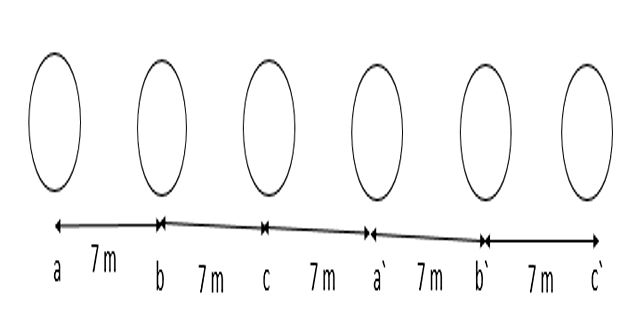
Solution-3

\[C_{n}=\dfrac{2\pi\varepsilon}{ln\left(\dfrac{D_{eq}}{D_{s}^{b}}\right)}~F/m\]

Note:

\[D_{s}^{b}=\begin{cases} \sqrt[4]{\left(r\times d\right)^{2}}=\sqrt{r\cdot d} & 2~\mbox{strand}\\ \sqrt[9]{\left(r\times d\times d\right)^{3}}=\sqrt[3]{r\cdot d} & 3~\mbox{strand}\\ \sqrt[16]{\left(r\times d\times d\times d\times\sqrt{2}\right)^{4}}=1.09\sqrt[4]{r\cdot d} & 4~\mbox{strand} \end{cases}\]

Given \(D=7 \mathrm{m}\) and \(r=0.0138 \mathrm{m}\)
\[\begin{array}{l} \text { Dca }=\sqrt[4]{14 \times 7 \times 14 \times 35}=14.803 \mathrm{m} \\ G M D=\sqrt[3]{14.803 \times 11.732^{2}}=12.706 \mathrm{m} \end{array}\]
Dbc Dab GMD:
\[\mathrm{Dsa}=\mathrm{Dsb}=\mathrm{Dsc}=\sqrt{0.0138 \times 21}=0.538 \mathrm{m}\]
GMR:

\[\begin{aligned} \text { Capacitance } \quad \mathrm{Cn}&=\frac{2 \pi \epsilon}{\ln \left(\frac{G M D}{G M R}\right)} \mathrm{F} / \mathrm{m} \\ &=\frac{2 \pi \times 8.854 \times 10^{-12}}{\ln \left(\frac{12.706}{0.528}\right)} \\ &=0.0175 \times 10^{-9} \mathrm{F} / \mathrm{m} \\ &=0.0175 \mu \mathrm{F} / \mathrm{km} \end{aligned}\]

\[\begin{aligned} \text { Susceptance } B &=314 \times 0.0175 \\ &=5.4919 \times 10^{-6} \mathrm{F} / \mathrm{km} \end{aligned}\]

Problem-4

A three-phase double-circuit line is shown in figure, the diameter of each conductor is 2.0 cm. The line is transposed & carries balanced load, the capacitance per phase to neutral of the line is?

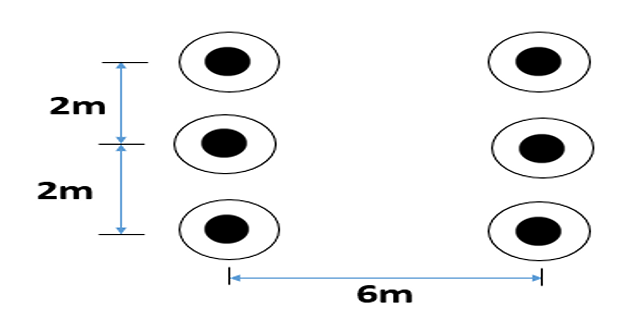
Solution-4

\[\begin{array}{c} r=0.01 m \\ D_{a b}=\sqrt{2 \times 6.32}=3.555=D_{b c} \\ D_{c a}=\sqrt{6 \times 4}=4.899 \\ D_{e q}=\sqrt[3]{D_{a b}} \times D_{b c} \times D_{c a}=3.955 m \end{array}\]

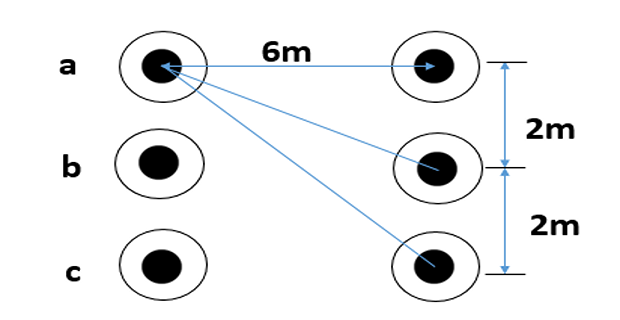
\[\begin{array}{l} \mathrm{D}_{\mathrm{sa}}=\sqrt{0.01 \times 7.21}=0.2685=\mathrm{D}_{\mathrm{sc}}\\ \mathrm{D}_{\mathrm{sb}}=\sqrt{0.01 \times 6.00}=0.2449 \\ \mathrm{D}_{\mathrm{s}}=\sqrt[3]{(0.2685)^{2} \times 0.2449}=0.261 \end{array}\]
Self GMD(calculated from the first transposition cycle)
\[\begin{array}{l} \mathrm{C}_{\mathrm{n}}=\frac{2 \pi \epsilon_{0} \epsilon_{r}}{\ln (d / r)} \\ =\frac{2 \pi \times 8.85 \times 10^{-12} \times 1}{\ln \left(\frac{3.955}{0.261}\right)} \\ =2.045 \times 10^{-11} \\ =0.02045 \mu \mathrm{F} / \mathrm{km} \end{array}\]
Capacitance to neutral

Problem-5

Consider a 500 kV, three-phase bundles conductor line as shown in the figure, what is the capacitive reactance to neutral in ohms/km at 50 Hz

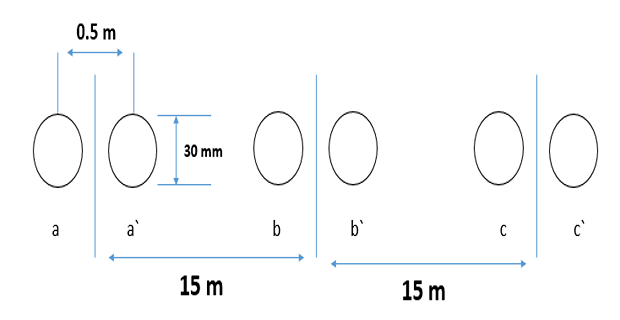
Solution-5

\[\begin{aligned} &\begin{array}{l} \mathrm{d}=15 \mathrm{m}, \quad \mathrm{S}=0.5 \mathrm{m}, \quad \mathrm{r}=0.015 \mathrm{m} \end{array} \end{aligned}\]
Given data:
GMD and GMR:

\[\begin{aligned} &\begin{array}{l} \mathrm{D}_{\mathrm{eq}}=\sqrt[3]{\mathrm{D}_{\mathrm{ab}} \times \mathrm{D}_{\mathrm{bc}} \times \mathrm{D}_{\mathrm{ca}}} \\ =\sqrt[3]{15 \times 15 \times 30}=18.89 \\ \mathrm{D}_{\mathrm{s}}=\sqrt{0.015 \times 0.5}=0.0866 \\ \end{array} \end{aligned}\]
Capacitance

\[\begin{aligned} \mathrm{C}_{\mathrm{n}}&=\frac{2 \pi \epsilon_{0} \epsilon_{r}}{\ln (d / r)} \\ &=\frac{2 \pi \times 8.85 \times 10^{-12} \times 1}{\ln \left(\frac{18.89}{0.0866}\right)}=0.0103 \mu \mathrm{F} / \mathrm{km} \end{aligned}\]