Demonstrative Video

Three-Phase Circuits

SECTION 01

Problem-1: Line and Phase Quantities

Determine the following quantities for the circuit shown

line currents
phase voltages of the load
line voltages of the load
phase voltages of the source
line voltages of the source

SECTION 02

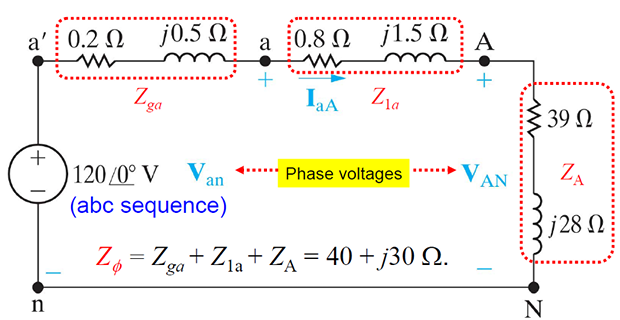
Solution-1

\[\begin{array}{l} \mathbf{I}_{a A}=\frac{\mathbf{V}_{a^{\prime} n}}{Z_{g a}+Z_{1 a}+Z_{A}}=\frac{120 \angle 0^{\circ}}{40+j 30}=\left(2.4 \angle-36.87^{\circ}\right) \mathrm{A} \\ \mathbf{I}_{b B}=\mathbf{I}_{a A}<-120^{\circ}=\left(2.4 \angle-156.87^{\circ}\right) \mathrm{A} \\ \mathbf{I}_{c C}=\mathbf{I}_{a A}<+120^{\circ}=\left(2.4 \angle+83.13^{\circ}\right) \mathrm{A} \end{array}\]

\[\begin{array}{l} \mathbf{V}_{A N}=\mathbf{I}_{a A} Z_{A}=\left(2.4 \angle-36.87^{\circ}\right)(39+j 28)=\left(115.22 \angle-1.19^{\circ}\right) \mathrm{V}\\ \mathbf{V}_{B N}=\mathbf{V}_{A N} \angle-120^{\circ}=\left(115.22 \angle-121.19^{\circ}\right) \mathrm{V} \\ \mathbf{V}_{C N}=\mathbf{V}_{A N} \angle+120^{\circ}=\left(115.22 \angle+118.81^{\circ}\right) \mathrm{V} \end{array}\]

The 3 line currents (of both load & source) are:

The 3 line voltages of the load are:

\[\begin{aligned} \mathrm{V}_{A B} &=\left(\sqrt{3} \angle 30^{\circ}\right) \mathbf{{V}_{A N}} \\ &=\left(\sqrt{3} \angle 30^{\circ}\right)\left(115.22 \angle-1.19^{\circ}\right) \\ &=\left(199.58<+28.81^{\circ}\right) \mathrm{V} \end{aligned}\]

\[\begin{aligned} \mathrm{V}_{B C} &=\mathbf{V}_{A B} \angle-120^{\circ} \\ &=\left(199.58 \angle-91.19^{\circ}\right) \mathrm{V} \\ \mathrm{{V}_{C A}} &=\mathbf{V}_{A B} \angle+120^{\circ} \\ &=\left(199.58 \angle+148.81^{\circ}\right) \mathrm{V} \end{aligned}\]

\[\begin{aligned} \mathbf{V}_{a n}=\mathbf{V}_{a^{\prime} \eta}-\mathbf{I}_{a A} Z_{g a} &=120-\left(2.4 \angle-36.87^{\circ}\right)(0.2+j 0.5) \\ =&\left(118.9 \angle-0.32^{\circ}\right) \mathrm{V} \\ \mathbf{V}_{b n}=& \mathbf{V}_{a n} \angle-120^{\circ}=\left(118.9 \angle-120.32^{\circ}\right) \mathrm{V} \\ \mathbf{V}_{c n}=& \mathbf{V}_{a n} \angle+120^{\circ}=\left(118.9 \angle+119.68^{\circ}\right) \mathrm{V} \end{aligned}\]

\[\begin{aligned} \mathbf{V}_{a b} &=\left(\sqrt{3} \angle 30^{\circ}\right)\mathrm{V_{a n}}=\left(\sqrt{3} \angle 30^{\circ}\right)\left(118.9 \angle-0.32^{\circ}\right) \\ &=\left(205.94 \angle+29.68^{\circ}\right) \mathrm{V} \\ \mathbf{V}_{b c} &=\mathbf{V}_{a b} \angle-120^{\circ}=\left(205.94 \angle-90.32^{\circ}\right) \mathrm{V} \\ \mathbf{V}_{c a} &=\mathbf{V}_{a b} \angle+120^{\circ}=\left(205.94 \angle+149.68^{\circ}\right) \mathrm{V} \end{aligned}\]

The 3 phase voltages of the source are:

SECTION 03

Problem-2: Complex power and Power Dissipation

The equivalent Y-Y configuration of a circuit is shown. Determine the complex powers provided by the source and dissipated by the line of a a-phase?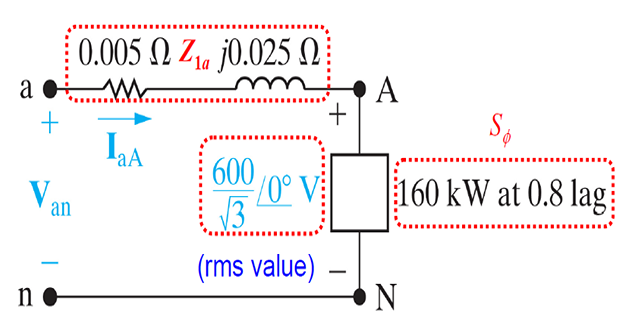

SECTION 04

Solution-2

\[\begin{aligned} S_{\phi}& =\mathbf{V}_{\phi} \mathbf{I}_{\phi}^{*}\\ \Rightarrow (160+j 120) 10^{3}&=\frac{600}{\sqrt{3}} \mathbf{I}_{a A}^{*} \\ \Rightarrow \mathbf{I}_{a A}& =\left(577.35 \angle-36.87^{\circ}\right) \mathrm{A} \end{aligned}\]

\[\begin{aligned} \mathbf{V}_{a n}& =\mathbf{V}_{A N}+\mathbf{I}_{a A} Z_{1 a} \\ &=600 / \sqrt{3}+\left(577.35 \angle-36.87^{\circ}\right)(0.005+j 0.025)\\ &=\left(357.51 \angle 1.57^{\circ}\right) \mathrm{V} \end{aligned}\]

The line current of a-phase can be calculated by the complex power is:

\[\begin{aligned} S_{a n} &=\mathbf{V}_{a n} \mathbf{I}_{a A}^{*}=\left(357.51 \angle 1.57^{\circ}\right)\left(577.35 \angle 36.87^{\circ}\right) \\ &=\left(206.41 \angle 38.44^{\circ}\right) \mathrm{kV} \mathrm{A} \end{aligned}\]

\[\begin{aligned} S_{a A} &=\left|\mathbf{I}_{a A}\right|^{2} Z_{1 a}=(577.35)^{2}(0.005+j 0.025) \\ &=\left(8.50 \angle 78.66^{\circ}\right) \mathrm{kV} \mathrm{A} \end{aligned}\]

The complex power provided by the source of aphase is:

SECTION 05

Problem-3: Star and Delta Configurations

Each phase of a three-phase alternator, generates a voltage of 3810.5 V and can carry a maximum current of 30 A.

Find the following quantities:

line current,
line voltage
total kVA capacity,

if the alternator is connected in

star configuration
delta configuration

SECTION 06

Solution-3

\(\text { Given data: }~~ E_{p h}=3810.5 \mathrm{V} ~~ I_{p h}=30 A\)

Star	Delta
\[\begin{aligned} \Rightarrow & \text{Line current}~ \mathrm{I}_{t} =\mathrm{I}_{\mathrm{ph}}=30 \mathrm{A} \\ \Rightarrow & \text{Line voltage} ~\mathrm{E}_{\ell} =\sqrt{3} \mathrm{E}_{\mathrm{ph}}\\ & =6600 \mathrm{V} \\ \Rightarrow & \text{Total}~ \mathrm{kVA} =\sqrt{3} \mathrm{E}_{l} \mathrm{I}_{l} \\ =&\sqrt{3} \times 6600 \times 30 \times 10^{-3} \\ &=342.95 \end{aligned}\]	\[\begin{aligned} \Rightarrow & \mathrm{I}_{\ell}=\sqrt{3} \mathrm{I}_{\mathrm{ph}}=51.96 \mathrm{A} \\ \Rightarrow & \mathrm{E}_{\ell}=3810.5 \mathrm{V} \\ \Rightarrow & \text { Total kVA }=\sqrt{3} \mathrm{E}_{l} \mathrm{I}_{l} \\ =&\sqrt{3} \times 3810.5 \times 51.96 \times 10^{-3} \\ &=342.95 \end{aligned}\]

SECTION 07

Problem-4: Balanced 3-phase System

A balanced \(3-\phi\) load connected in star consists of \((6 + j 8)~\Omega\) impedance in each phase. It is connected to a \(3-\phi\) supply of 400 V, 50 Hz.

Find the following quantities:

magnitude of phase current
magnitude of line current
per phase power
total power.

Repeat the problem with the load impedance connected in delta

SECTION 08

Solution-4

\[\begin{aligned} E_{ph}& =400 / \sqrt{3}=230.94 \mathrm{V}\\ Z&=(6+j 8) \Omega=10 \angle 53.13^{\circ} \Omega \\ \mathrm{I}_{\mathrm{ph}}&=230.94 / 10=23.094 \mathrm{A} \\ \end{aligned}\]

\[\begin{aligned} \mathrm{I}_{\ell}&=\mathrm{I}_{\mathrm{ph}}=23.094 \mathrm{A}\\ P_{1-\phi}&=E_{p h} I_{p h} \cos \theta\\ =&230.94 \times 23.094 \times \cos 53.13^{\circ}\\ & =3200 \mathrm{W} \end{aligned}\]

\[\begin{aligned} \mathrm{P}_{\mathrm{T}}&=\sqrt{3} \mathrm{E}_{l} \mathrm{I}_{l} \cos \theta \\ =&\sqrt{3} \times 400 \times 23.094 \times \cos 53.13^{\circ}\\ &=9600 \mathrm{W} \\ \text{or}~\mathrm{P}_{\mathrm{T}}&=3 \mathrm{P}=9600 \mathrm{W} \end{aligned}\]

SECTION 09

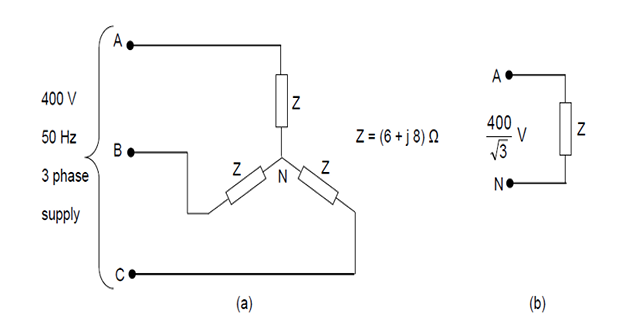
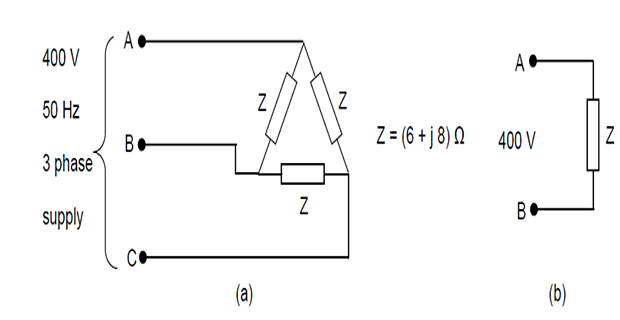
\(E_{p h}=400 ~\mathrm{V} \quad Z=(6+j 8) \Omega=10 \angle 53.13^{\circ} \Omega\)
Phase current, \(\mathrm{I}_{\mathrm{ph}}=400 / 10=40 \mathrm{A}\)
Line current, \(\mathrm{I}_{\ell}=\sqrt{3} \mathrm{I}_{\mathrm{ph}}=69.282 \mathrm{A}\)
Per phase power, \(P=E_{p h} I_{p h} \cos \theta=400 \times 40 \times \cos 53.13^{\circ}=9600 \mathrm{W}\)
Total power, \(\mathrm{P}_{T}=\sqrt{3} \mathrm{E}_{\ell} \mathrm{I}_{\ell} \cos \theta=\sqrt{3} \times 400 \times 69.282 \times \cos 53.13^{\circ}=28800 \mathrm{W}\)
Alternatively, total power, \(\mathrm{P}_{\mathrm{T}}=3 \mathrm{P}=28800 \mathrm{W}\)

SECTION 10

Problem-5: Phase Sequence

\[\begin{aligned} \mathrm{V}_{\mathrm{AN}} & =400 \cos \left(\omega \mathrm{t}-10^{\circ}\right) \mathrm{V} \\ \mathrm{v}_{\mathrm{BN}} & =400 \cos \left(\omega \mathrm{t}-250^{\circ}\right) \mathrm{V} \\ \mathrm{v}_{\mathrm{CN}} & =400 \cos \left(\omega \mathrm{t}-130^{\circ}\right) \mathrm{V} \end{aligned}\]

Determine the phase sequence of the set of voltages given by

SECTION 11

Solution-5

Given voltage phasors are:

\[\begin{aligned} \mathrm{V}_{\mathrm{AN}}=282.8 \angle-10^{\circ} \\ \mathrm{V}_{\mathrm{BN}}=282.8 \angle-250^{\circ}\\ \mathrm{V}_{\mathrm{CN}}=282.8 \angle-130^{\circ} \end{aligned}\]

Note: \(\mathrm{V}_{\mathrm{C}}\) is lagging \(\mathrm{V}_{\mathrm{A}}\). Hence phase sequence is \(\mathrm{ACB}\)

SECTION 12

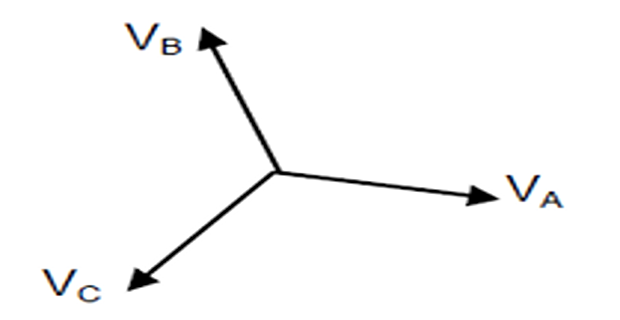
Problem-6: Balanced System & Phase Sequence

In a three-phase balanced supply, voltage \(\mathrm{V}_{\mathrm{C}}=110 \angle 65^{\circ} \mathrm{V}\).

Taking the phase sequence as \(\mathrm{ABC}\), find

the phase voltage
the line voltages

SECTION 13

Solution-6

\[\begin{aligned} \mathrm{V_A}& =\mathrm{Vc} \times 1 \angle-120^{\circ}=110 \angle-55^{\circ} \mathrm{V} \\ \mathrm{V_B}& =\mathrm{Vc} \times 1 \angle 120^{\circ}=110 \angle 185^{\circ} \mathrm{V} \\ \mathrm{V_C}& =110 \angle 65^{\circ} \mathrm{V} \end{aligned}\]

\[\begin{aligned} \mathrm{V_{AB}}& =\mathrm{V_A}-\mathrm{V_B}=190.5 \angle-25^{\circ} \mathrm{V} \\ \mathrm{V_{BC}}& =\mathrm{V_B}-\mathrm{V_C}=190.5 \angle-145^{\circ} \mathrm{V} \\ \mathrm{V_{CA}}&=\mathrm{V_C}-\mathrm{VA}=190.5 \angle 95^{\circ} \mathrm{V} \end{aligned}\]

SECTION 14

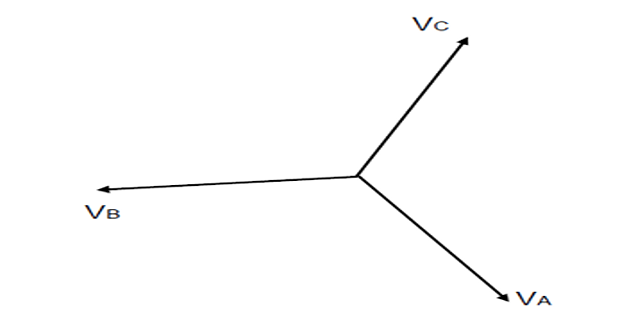
Problem-7: Unbalanced Delta System

\[\mathrm{Z}_{\mathrm{AB}}=10 \angle 0^{\circ} \Omega ;~ \mathrm{Z}_{\mathrm{BC}}=10 \angle 30^{\circ} \Omega;~ \mathrm{Z}_{\mathrm{CA}}=15 \angle-30^{\circ} \Omega\]

\(\checkmark\)

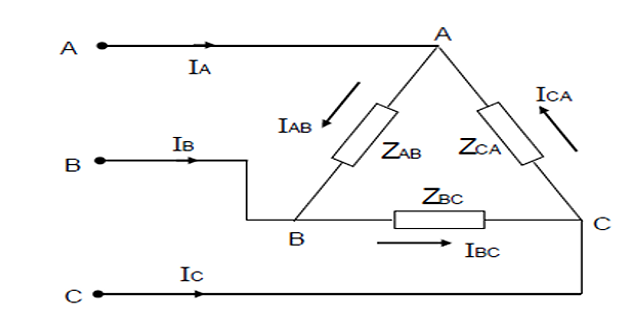
line voltages
phase currents
line currents
the real power consumed by the load.

\(\mathrm{V_{BC}}\) ABC system has a delta-connected load with impedances 3-wire A

SECTION 15

Solution-7

\[\begin{aligned} \mathrm{V}_{\mathrm{BC}}&=240 \angle 0^{\circ} \mathrm{V}\\ \mathrm{V} \mathrm{CA} & =240 \angle-120^{\circ} \mathrm{V}\\ \mathrm{V}_{\mathrm{AB}}&=240 \angle-240^{\circ} \mathrm{V} \end{aligned}\]

\[\begin{aligned} \mathrm{Z}_{\mathrm{AB}}&=10 \angle 0^{\circ} \Omega \\ \mathrm{Z}_{\mathrm{BC}}&=10 \angle 30^{\circ} \Omega\\ \mathrm{Z}_{\mathrm{CA}}&=15 \angle-30^{\circ} \Omega \end{aligned}\]

\[\begin{aligned} \mathrm{I_{BC}}&=\frac{\mathrm{V}_{\mathrm{BC}}}{\mathrm{Z}_{\mathrm{BC}}}=\frac{240 \angle 0^{\circ}}{10 \angle 30^{\circ}}=24 \angle-30^{\circ} \mathrm{A}=(20.7846-\mathrm{j} 12) \mathrm{A}\\ \mathrm{I_{CA}}& = \frac{\mathrm{V}_{\mathrm{CA}}}{\mathrm{Z}_{\mathrm{CA}}}=\frac{240 \angle-120^{\circ}}{15 \angle-30^{\circ}}=16 \angle-90^{\circ} \mathrm{A}=(0-\mathrm{j} 16) \mathrm{A}\\ \mathrm{I_{AB}}&==\frac{\mathrm{V}_{\mathrm{AB}}}{\mathrm{Z}_{\mathrm{AB}}}=\frac{240 \angle-240^{\circ}}{10 \angle 0^{\circ}}=24 \angle-240^{\circ} \mathrm{A}=(-12+\mathrm{j} 20.7846) \mathrm{A} \end{aligned}\]

Phase currents are:

\[\begin{aligned} \mathrm{I_A}& =\mathrm{I}_{\mathrm{AB}}-\mathrm{I}_{\mathrm{CA}}=(-12+\mathrm{j} 20.7846)-(-\mathrm{j} 16)\\ & =(-12+\mathrm{j} 36.7846)=38.6925 \angle 108.07^{\circ} \mathrm{A}\\ \mathrm{I_B}&=\mathrm{I}_{\mathrm{BC}}-\mathrm{I}_{\mathrm{AB}}=(32.7846-\mathrm{j} 32.7846)=46.3644 \angle-45^{\circ} \mathrm{A}\\ \mathrm{I_C}&=\mathrm{I_{CA}}-\mathrm{I_{BC}}=(-20.7846-\mathrm{j} 4)=21.166 \angle-169.11^{\circ} \mathrm{A} \end{aligned}\]

. Thus and at junction Line currents are obtained by applying

\[\begin{aligned} \mathrm{R}_{\mathrm{AB}}&=10 ~\Omega \\ \mathrm{R}_{\mathrm{BC}}&=10 \cos 30^{\circ}=8.6603 ~\Omega \\ \mathrm{R}_{\mathrm{CA}}&=15 \cos 30^{\circ}=12.9904 ~\Omega \end{aligned}\]

\[\begin{aligned} &= \left(24^{2} \times 10\right)+\left(24^{2} \times 8.6603\right)+\left(16^{2} \times 12.9904\right)\\ &=14073.8 \mathrm{W}=14.0738 \mathrm{kW} \end{aligned}\]

Real power consumed by the load :

SECTION 16

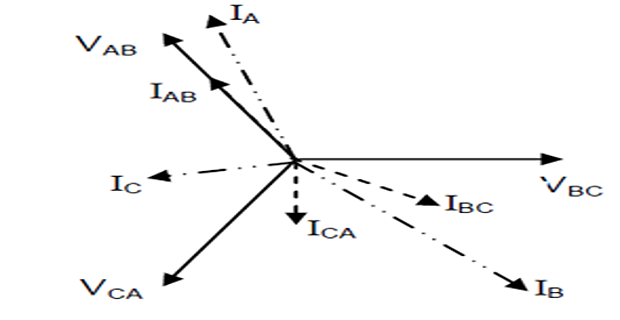
Problem-8: Unbalanced Star System

A \(3-\phi\), 4 -wire, \(208~\mathrm{V}\) system has a star connected load with impedances

\[\mathrm{Z}_{\mathrm{A}}=6 \angle 0^{\circ} \Omega ;~ \mathrm{Z}_{\mathrm{B}}=6 \angle 30^{\circ} \Omega;~ \mathrm{Z}_{\mathrm{C}}=5 \angle 45^{\circ} \Omega\]

Taking the voltage \(\mathrm{V_{AN}}\) as reference, determine line and neutral currents. Draw the phasor diagram. Also calculate the real power consumed by the load.

SECTION 17

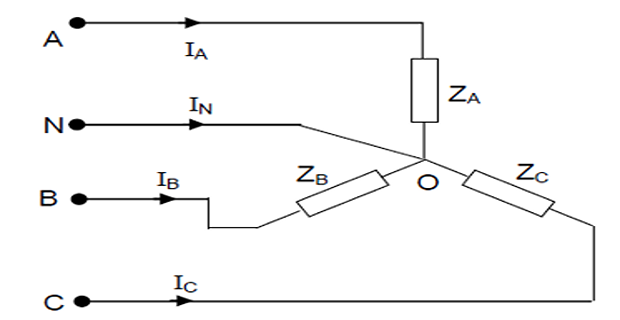
Solution-8

\(\mathrm{Z}_{\mathrm{A}}=6 \angle \mathrm{0}^{\circ} \Omega ;~ \mathrm{Z}_{\mathrm{B}}=6 \angle 30^{\circ} \Omega\); \(\mathrm{Z}_{\mathrm{C}}=5 \angle 45^{\circ} \Omega\)

Taking the phase sequence as ABC,

\[\begin{aligned} \mathrm{V}_{\mathrm{AN}}&=\frac{208}{\sqrt{3}} \angle 0^{\circ} V\\ &=120.08 \angle 0^{\circ} \mathrm{V}\\ \mathrm{V}_{\mathrm{BN}}&=120.08 \angle-120^{\circ} \mathrm{V}\\ \mathrm{V}_{\mathrm{CN}}&=120.08 \angle-240^{\circ} \mathrm{V} \end{aligned}\]

\[\begin{aligned} \mathrm{I}_{\mathrm{A}}&=\frac{\mathrm{V}_{\mathrm{AN}}}{\mathrm{Z}_{\mathrm{A}}}=\frac{120.08}{6 \angle 0^{\circ}}\\ &=20.01 \angle 0^{\circ} \mathrm{A}\\ \mathrm{I}_{\mathrm{B}}&=\frac{\mathrm{V}_{\mathrm{BN}}}{\mathrm{Z}_{\mathrm{B}}}=\frac{120.08 \angle-120^{\circ}}{6 \angle 30^{\circ}}\\ &=20.01 \angle-150^{\circ} \mathrm{A}\\ \mathrm{I}_{\mathrm{C}}&=\frac{V_{C N}}{Z_{C}}=\frac{120.08 \angle-240^{\circ}}{5 \angle 45^{\circ}}\\ &=24.01 \angle 75^{\circ} \mathrm{A} \end{aligned}\]

\[\begin{aligned} I_{N}&=-\left(I_{A}+I_{B}+I_{C}\right)\\ &=(-8.89-j 13.19) A\\ &=15.91 \angle-124^{\circ} A \end{aligned}\]

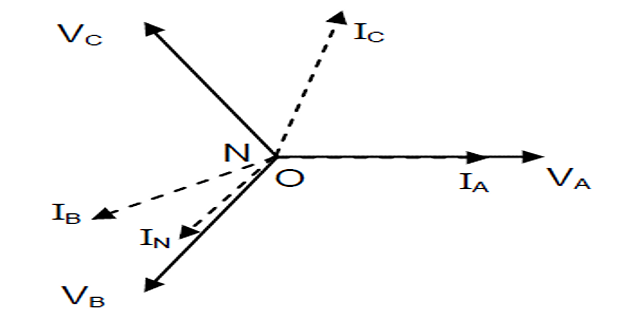
Resistances in different phases are:

\(\mathrm{R}_{\mathrm{A}}=6 \Omega ~~ \mathrm{R}_{\mathrm{B}}=6 \cos 30^{\circ}=5.1962 \Omega ~~ \mathrm{R}_{\mathrm{C}}=3.53 \Omega\)

\[\begin{aligned} =& \left(20.01^{2} \times 6\right)+\left(20.01^{2} \times 5.19\right)+\left(24.01^{2} \times 3.53\right) \\ =&6524.58~ \mathrm{W}= 6.5246 ~\mathrm{kW} \end{aligned}\]

Real power consumed by the load

SECTION 18

Problem-9: Unbalanced Systems

A \(3-\phi\), 3-wire, 208 V, ACB system has star connected load with impedances \(\mathrm{Z}_{\mathrm{A}}=6 \angle 0^{\circ} \Omega ; ~ \mathrm{Z}_{\mathrm{B}}=6 \angle 30^{\circ} \Omega\) and \(\mathrm{Zc}=5 \angle 45^{\circ} \Omega .\) Taking \(\mathrm{V}_{\mathrm{BC}}\) as reference, Determine

line currents
the voltage across load impedances

SECTION 19

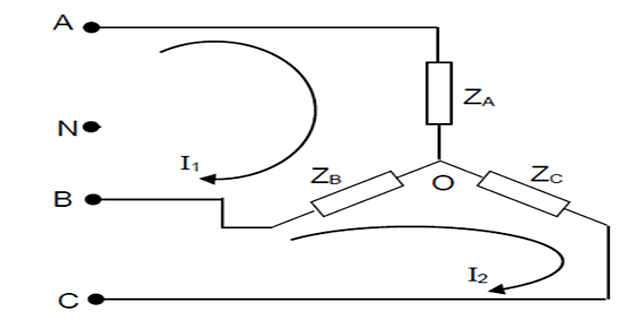
Solution-9

\[\begin{aligned} \mathrm{V}_{\mathrm{BC}}&=208 \angle \mathrm{0}^{\circ} \mathrm{V} \\ \quad \mathrm{V}_{\mathrm{CA}}&=208 \angle 120^{\circ} \mathrm{V} \\ \quad \mathrm{V}_{\mathrm{AB}}&=208 \angle-120^{\circ} \mathrm{V} \end{aligned}\]

\[\begin{aligned} Z_{A}&=6 \Omega \\ Z_{B}&=(5.1962+j 3) \Omega \\ Z_{C}&=(3.5355+j 3.5355) \Omega \end{aligned}\]

\(\left[\begin{array}{cc}Z_{A}+Z_{B} & -Z_{B} \\ -Z_{B} & Z_{B}+Z_{c}\end{array}\right]\left[\begin{array}{l}I_{1} \\ I_{2}\end{array}\right]=\left[\begin{array}{c}V_{A B} \\ V_{B C}\end{array}\right]\) \(\left[\begin{array}{cc}11.1962+j 3 & -5.1962-j 3 \\ -5.1962-j 3 & 8.7317+j 6.5355\end{array}\right]\left[\begin{array}{l}I_{1} \\ I_{2}\end{array}\right]=\left[\begin{array}{c}208 \angle-120^{\circ} \\ 208 \angle 0^{\circ}\end{array}\right]\)

Determinant of the coefficient matrix \(= 90.9323 \angle 48.580\)

\(\left[\begin{array}{l}\mathrm{I}_{1} \\ \mathrm{I}_{2}\end{array}\right]=\frac{1}{90.9323 \angle 48.58^{\circ}}\left[\begin{array}{cc}8.7317+\mathrm{j} 6.5355 & 5.1962+\mathrm{j} 3 \\ 5.1962+\mathrm{j} 3 & 11.1962+\mathrm{j} 3\end{array}\right]\left[\begin{array}{c}208 \angle-120^{\circ} \\ 208 \angle 0^{\circ}\end{array}\right]\) \(=\left[\begin{array}{c}-3.6097-\mathrm{j} 22.9799 \\ 11.7974-\mathrm{j} 23.7446\end{array}\right]=\left[\begin{array}{l}23.2617 \angle-98.93^{\circ} \\ 26.5139 \angle-63.58^{\circ}\end{array}\right]\)

\(\left[\begin{array}{l}\mathrm{I}_{1} \\ \mathrm{I}_{2}\end{array}\right]=\left[\begin{array}{l}-3.6097-\mathrm{j} 22.9799 \\ 11.7974-\mathrm{j} 23.7446\end{array}\right]\)

From the mesh currents, line currents can be calculated:

\(\mathrm{I}_{\mathrm{A}}=\mathrm{I}_{1}=(-3.6109-\mathrm{j} 22.9797) \mathrm{A}=23.2617 \angle-98.93^{\circ} \mathrm{A}\) \(\mathrm{I}_{B}=\mathrm{I}_{2}-\mathrm{I}_{1}=(15.4071-\mathrm{j} 0.7647) \mathrm{A}=15.426 \angle-2.84^{\circ} \mathrm{A}\) \(\mathrm{I_C}=-\mathrm{I}_{2}=(-11.7974+\mathrm{j} 23.7446) \mathrm{A}=26.5139 \angle 116.42^{\circ} \mathrm{A}\)

Voltages across the loads can be calculated as:

\(\mathrm{V}_{\mathrm{AO}}=\mathrm{Z}_{\mathrm{A}} \mathrm{I}_{\mathrm{A}}=(-21.6654-\mathrm{j} 137.8782) \mathrm{A}=139.5702 \angle-98.93^{\circ} \mathrm{V}\) \(\mathrm{V}_{\mathrm{BO}}=\mathrm{Z}_{\mathrm{B}} \mathrm{I}_{\mathrm{B}}=(82.3503+\mathrm{j} 42.2497) \mathrm{A}=92.556 \angle 27.16^{\circ} \mathrm{V}\) \(\mathrm{V}_{\mathrm{CO}}=\mathrm{Z}_{\mathrm{C}} \mathrm{I_C}=(-125.6599+\mathrm{j} 42.2404) \mathrm{A}=132.5695 \angle 161.42^{\circ} \mathrm{V}\)

SECTION 20

Problem-10: Power measurement by two-watt meter

The power input to a \(2000 ~V, 50 \mathrm{Hz},\) 3-phase motor is measured by two wattmeters which indicate \(100 \mathrm{kW}\) and \(300 \mathrm{kW}\) respectively. Calculate

the input power
the power factor
the line current.

SECTION 21

Solution-10

Given : \(\quad \mathrm{W}_{1}=100 ~\mathrm{kW}\) and \(\mathrm{W}_{2}=300~ \mathrm{kW}\)
Input power: \(\mathrm{P}=\mathrm{W}_{1}+\mathrm{W}_{2}=400~ \mathrm{kW}\)
Power factor angle

\[\begin{aligned} \quad \tan \theta& =\sqrt{3} \frac{\mathrm{W}_{2}-\mathrm{W}_{1}}{\mathrm{W}_{1}+\mathrm{W}_{2}}\\ &=\sqrt{3} \times \frac{200}{400}=0.8660\\ \theta& =40.89^{\circ} \\ \cos \theta&=0.7559 \end{aligned}\]
Power factor \(=0.7559\) lagging
Three-phase power, \(P=\sqrt{3} V_{l} I_{l} \cos \theta\)
Line current, \(\mathrm{I}_{l}=\frac{400 \times 10^{3}}{\sqrt{3} \times 2000 \times 0.7559}=152.76 \mathrm{A}\)

SECTION 22

Problem-11: Power measurement by two-watt meter

Two watt meters are connected to measure the power in a 3-phase 3-wire balanced load. Determine the total power and power factor, if the two watt-meters read

\(1000 \mathrm{W}\) each, both positive
\(1000 \mathrm{W}\) each of opposite sign.

SECTION 23

Solution-11

Case-1: Given data: \(\quad \mathrm{W}_{1}=1000~ \mathrm{W} ; \quad \mathrm{W}_{2}=1000 \mathrm{W}\)
- Total power \(\mathrm{P}=\mathrm{W}_{1}+\mathrm{W}_{2}=2000 \mathrm{W}\)
- \(\tan \theta=\sqrt{3} \frac{\mathrm{W}_{2}-\mathrm{W}_{1}}{\mathrm{W}_{1}+\mathrm{W}_{2}}=0\)
- Power factor angle \(\theta=0\)
- Power factor \(=\cos 0^{\circ}=1.0\)
Case-2: Given data: \(\quad \mathrm{W}_{1}=-1000 \mathrm{W} ; \quad \mathrm{W}_{2}=1000 \mathrm{W} ; \quad\)
- Total power \(\mathrm{P}=\mathrm{W}_{1}+\mathrm{W}_{2}=0\)
- \(\tan \theta=\sqrt{3} \frac{W_{2}-W_{1}}{W_{1}+W_{2}}=\infty ;\)
- Power factor angle \(\theta=90^{\circ}\)
- Power factor = 0 lagging.

SECTION 24

Problem-12: Power measurement by two-watt meter

Across \(400 \mathrm{V}, 3\) -phase supply mains, a star-connected balanced load of \((16+\mathrm{j} 12) \Omega\) impedance is connected.

Taking \(V_a\) as reference, determine the line currents and the power absorbed by the load
If two wattmeters are used to measure the power, what will be the readings of the wattmeters?

SECTION 25

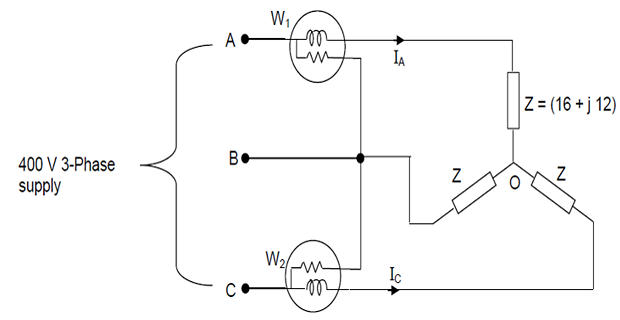
Solution-12

\(\quad V_{A}=\frac{400}{\sqrt{3}} \angle 0^{\circ}=230.94 \angle 0^{\circ}~V ~~ Z=(16+j 12)=20 \angle 36.87^{\circ} \Omega\)
\[\begin{aligned} \mathrm{I}_{\mathrm{A}}&=\frac{\mathrm{V}_{\mathrm{A}}}{\mathrm{Z}}=11.54 \angle-36.87^{\circ} \mathrm{A} \\ \mathrm{I}_{\mathrm{B}}&=11.54 \angle-156.87^{\circ} \mathrm{A}\\ \mathrm{I}_{\mathrm{C}}&=11.54 \angle 83.13^{\circ} \mathrm{A} \end{aligned}\]
Line currents are:
\[P=\sqrt{3} V_{l} I_{l} \cos \theta=\sqrt{3} \times 400 \times 11.54 \cos 36.87^{\circ}=6400 \mathrm{W}\]
Total power
\[\begin{aligned} \quad \mathrm{W}_{1}&=\sqrt{3} \mathrm{V}_{\text {ph }} \mathrm{I}_{\text {ph }} \cos \left(\theta+30^{\circ}\right)\\ &=\sqrt{3} \times 230.94 \times 11.54 \cos 66.87^{\circ}=1814.35 \mathrm{W}\\ \mathrm{W}_{2}&=\sqrt{3} \mathrm{V}_{\mathrm{ph}} \mathrm{I}_{\mathrm{ph}} \cos \left(\theta-30^{\circ}\right)\\ & =\sqrt{3} \times 230.94 \times 11.54 \cos 6.87^{\circ}=4585.64 \mathrm{W} \end{aligned}\]
Watt meter readings: