Power System Stability Solved Problems
Demonstrative Video
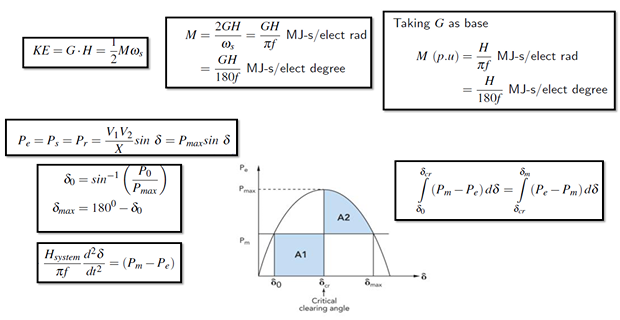
Revision of important Concepts & Formulas
Problem-1
A 4 -pole, \(60 \mathrm{~Hz}, 30\) MVA synchronous generator is having the inertia constant 8 MJ/MVA. The input power and output power of the generator are found to be \(25 \mathrm{MW}\) and \(18 \mathrm{MW}\), respectively. Calculate
the kinetic energy stored in the rotor at synchronous speed
accelerating power
acceleration
torque angle at 10 cycles
Solution-1
- \[K E=30 \times 8=240 \mathrm{MJ}\]The kinetic energy stored in the rotor ,
- \[P_{a}=P_{m}-P_{e}=25-18=7 \mathrm{MW}\]The accelerating power
- \[M=\frac{2 H S_{b}}{\omega_{s m}}=\frac{H S_{b}}{\pi f}=\frac{8 \times 30}{\pi \times 60}=1.27\]The acceleration
- \[\frac{2 \times 1.27}{4} \frac{d^{2} \delta}{d t^{2}}=7 \Rightarrow \frac{d^{2} \delta}{d t^{2}}=11.02 \mathrm{rad} / \mathrm{s}^{2}\]Substituting necessary values
- \[t=\frac{10}{60}=0.166 \mathrm{~s}\]The torque angle at 10 cycles
- \[2 \frac{d \delta}{d t} \times \frac{d^{2} \delta}{d t^{2}}=11.02 \times 2 \frac{d \delta}{d t}\]yields, Multiply both sides by
- \[\begin{array}{c} \int 2 \frac{d \delta}{d t} \times \frac{d^{2} \delta}{d t^{2}} d t=22.04 \int \frac{d \delta}{d t} d t \\ \left(\frac{d \delta}{d t}\right)^{2}=22.04 \delta+C \end{array}\]Integrating
- \[\left(\frac{d \delta}{d t}\right)^{2}=22.04 \delta \Rightarrow \frac{d \delta}{d t}=4.69 \delta^{0.5}\]and At
- \[\begin{array}{c} \int \delta^{-0.5} d \delta=4.69 \int d t \\ \frac{\delta^{-0.5+1}}{-0.5+1}=4.69 t \\ \delta^{0.5}=2.34 t \\ \delta=(2.34 t)^{2}=(2.34 \times 0.166)^{2}=0.15 \mathrm{rad} \end{array}\]Integrating
Practice Problem-1
The stored energy in the rotor of a 4-pole, \(50 \mathrm{~Hz}, 25 \mathrm{MVA}\) synchronous generator is found to be \(180 \mathrm{MJ}\). The input power and output power of the generator are written as \(35 \mathrm{MW}\) and \(28 \mathrm{MW}\), respectively. Calculate
the inertia constant,
accelerating power,
acceleration.
Problem-2
A synchronous machine is having the inertia constant \(6 \mathrm{MJ} / \mathrm{MVA}\). The machine is connected to an infinite bus through a transmission line. The generator delivers a real power of \(0.9\) per unit at a \(0.9\) power factor lagging to the infinite bus. A small disturbance occurs in the system, and the deviation of the torque angle is found to be \(9^{\circ} .\) Calculate
the per unit apparent power,
line current,
generated voltage,
synchronizing power coefficient,
undamped angular frequency of oscillation,
period of oscillation.
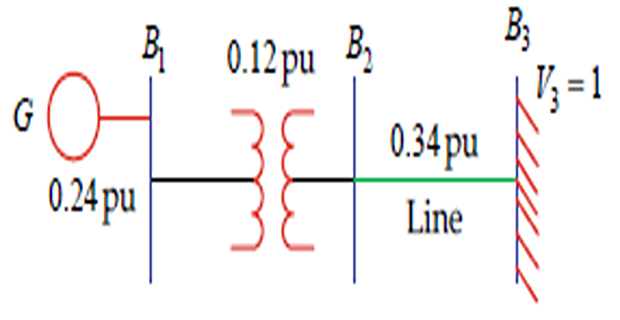
Solution-2

- \[X=j(0.24+0.12+0.34)=j 0.70\]The reactance between the generator and finite bus
- \[S=\frac{0.9}{0.9}\left\lfloor\cos ^{-1} 0.9=1\left\lfloor 25.84^{\circ}\right.\right.\]The value of the apparent power
- \[I_{L}=\frac{S^{*}}{V_{2}^{*}}=\frac{1\left\lfloor-25.84^{\circ}\right.}{1.0\left\lfloor 0^{\circ}\right.}=1\left\lfloor-25.84^{\circ} \mathrm{pu}\right.\]The value of the line current
The value of the generated voltage \(E_{g}=V_{2}+I_{L} X=1+0.70\left\lfloor 90^{\circ} \times 1\left\lfloor-25.84^{\circ}=1.45\left\lfloor 25.76^{\circ} \mathrm{pu}\right.\right.\right.\)
- \[S_{p}=P_{\max } \cos \delta_{0}=\frac{1.45 \times 1}{0.70} \cos \left(25.76^{\circ}-9^{\circ}\right)=1.98\]The synchronizing power coefficient
- \[\omega_{n}=\sqrt{\frac{\omega_{s}}{2 H} S_{p}}=\sqrt{\frac{\pi \times 50}{6} \times 1.98}=7.2 \mathrm{rad} / \mathrm{s}\]The undamped angular frequency
- \[f_{n}=\frac{7.2}{2 \pi}=1.14 \mathrm{~Hz}\]The frequency of oscillation
- \[T=\frac{1}{f_{n}}=\frac{1}{1.14}=0.88 \mathrm{~s}\]The period of oscillation
Practice problem-2
A \(50 \mathrm{~Hz}\) synchronous machine is having the inertia constant of \(8 \mathrm{MJ} / \mathrm{MVA}\) and the excitation voltage \(E_{f}=1.5\left\lfloor 20^{\circ}\right.\) pu. The generator is connected to an infinite bus through a transmission line, and the infinity bus voltage is \(V_{i b}=1\left\lfloor 0^{\circ} \mathrm{pu}\right.\). The total reactance between the generator and the infinite bus is found to be \(0.23\) pu. Find
the synchronizing power coefficient,
undamped angular frequency of oscillation,
frequency of oscillation,
period of oscillation.