Power System Stability Solved Problems
Demonstrative Video
Problem-1
A \(50 \mathrm{~Hz}\) four-pole turbogenerator rated \(20 \mathrm{MVA}, 13.2 \mathrm{kV}\) has an inertia constant of \(H=9.0 \mathrm{~kW}-\mathrm{sec} / \mathrm{kVA}\).
Determine the K.E. stored in the rotor at synchronous speed.
Determine the acceleration if the input less the rotational losses is 25000 HP and the electric power developed is \(15000 \mathrm{~kW}\).
If the acceleration computed for the generator is constant for a period of 15 cycles,
determine the change in torque angle in that period and the r.p.m. at the end of 15 cycles.
Assume that the generator is synchronized with a large system and has no accelerating torque before the 15 cycle period begins.
Solution-1
- \[\begin{aligned} H&=\frac{\text { K.E. Stored energy in megajoules }}{\text { Machine rating in MVA }}\\ \text{KE. in MJ} &=H \times \text{Machine rating in MVA}\\ & =9 \times 20=180~\mathrm{MJ} \end{aligned}\]Since
- \[\begin{aligned} P_{a} &=P_{i}-P_{G} \\ &=25000 \times 0.735-15000 \\ &=18375-15000=3375 \mathrm{~kW}=3.375 \mathrm{MW} \end{aligned}\]We know
- \[\begin{aligned} \frac{d^{2} \delta}{d t^{2}} &=\frac{P_{a}}{M}=\frac{3.375}{M} \\ M &=\frac{G H}{\pi f}=\frac{20 \times 9}{\pi \times 50}=1.146 \text { megajoules-sec/radian } \\ \therefore \quad \frac{d^{2} \delta}{d t^{2}} &=\frac{3.375}{1146}=2.945 \mathrm{rad} / \mathrm{sec}^{2} \quad \text { Ans. } \end{aligned}\]Now the acceleration is
- \[\begin{aligned} \dfrac{d^{2} \delta}{d t^{2}}=\dfrac{P_{a}}{M}=\text { constant }=2.945 \\ \dfrac{2 d \delta}{d t} \cdot \dfrac{d^{2} \delta}{d t^{2}} d t=2 \times 2.945 \dfrac{d \delta}{d t} d t \\ \left(\dfrac{d \delta}{d t}\right)^{2}=5.89 \delta+A \end{aligned}\]Using swing equation,
- \[\begin{aligned} \therefore \quad \dfrac{d \delta}{d t} &=\sqrt{5.89} \sqrt{\delta} \\ \frac{d \delta}{\sqrt{\delta}} &=\sqrt{5.89} d t \\ \delta^{-1 / 2} d \delta &=2.427 d t \\ 2 \delta^{1 / 2} &=2.427 t\\ \delta^{1 / 2} &=1.2135 t \\ \delta &=1.47258 \times t^{2} \\ \end{aligned}\]Since at
- \[\delta=1.47258 \times 0.09=0.1325 \text{radian} =7.5955 ~\text{electrical degrees}\]Now
Problem-2
A \(50 \mathrm{~Hz}\) synchronous generator is connected to an infinite bus through a line. The p.u. reactances of generator and the line are \(j 0.3\) p.u. and \(j 0.2\) p.u. respectively. The generator no load voltage is \(1.1\) p.u. and that of infinite bus is \(1.0\) p.u. The inertia constant of the generator is \(3 \mathrm{MW}\) -sec/MVA. Determine the frequency of natural oscillations if the generator is loaded to
\(60 \%\)
\(75 \%\)
of its maximum power transfer capacity and small perturbation in power is given
Solution
Since the system is operating initially under steady state condition, a small perturbation in power will make the rotor oscillate.
- \[f_{n}=\sqrt{\dfrac{\left.\frac{\partial P_{e}}{\partial \delta}\right|_{\delta_{0}}}{M}}\]The natural frequency of oscillation is given by
- \[\begin{aligned} \dfrac{\partial P_{e}}{\partial \delta}&=\frac{V_{1} V_{2}}{X} \cos \delta\\ &=\frac{1.1 \times 1}{0.5} \cos \delta_{0} \\ &=\frac{1.1 \times 1}{0.5} \times 0.8 \\ &=1.76 \\ \text { (Since } \sin \delta_{0} & \left.=\frac{0.6}{1}=0.6\right) \\ M &=\frac{G H}{\pi f}=\frac{1 \times 3}{50 \pi} = 0.019\\ f_{n} &=\sqrt{1.76/0.019}=9.6 \mathrm{rad} / \mathrm{sec} \\ &=1.53 \mathrm{~Hz} \end{aligned}\]\(60 \%\)
- \[\begin{aligned} \sin \delta_{0}&=0.75 \Rightarrow \delta_{0}=0.848 \mathrm{rad} \\ \frac{\partial P_{e}}{\partial \delta} \mid \delta_{0}&=\frac{1.1 \times 1}{0.5} \times 0.6614=1.455 \\ \therefore \quad f_{n}&=\sqrt{1.455/0.019}=8.750~ \mathrm{rad} \mathrm{sec} . \\ &=1.39 \mathrm{~Hz} \text { Ans. } \end{aligned}\]\(75 \%\)
Problem-3
If a 3-phase fault has occurred at point \(\mathrm{P}\), find the critical clearing
angle for clearing the fault with simultaneous opening of the breakers 1
and 2 . The reactance values are indicated and the generator is
delivering \(1.0\) pu power at the
instant proceeding the fault.
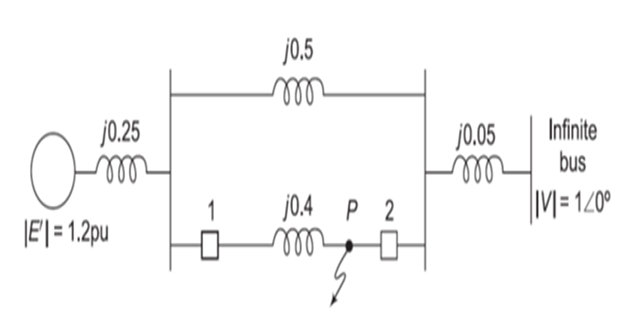
- \[\begin{aligned} X_{\mathrm{I}} &=0.25+\frac{0.5 \times 0.4}{0.5+0.4}+0.05 \\ &=0.522 \mathrm{pu} \\ P_{\mathrm{eI}} &=\frac{\left|E^{\prime}\right||V|}{X_{l}} \sin \delta=\frac{1.2 \times 1}{0.522} \sin \delta \\ &=2.3 \sin \delta \end{aligned}\]Normal operation (prefault)

- \[\begin{aligned} 1.0 &=2.3 \sin \delta_{0} \\ \delta_{0} &=25.8^{\circ}=0.45 \text { radians } \end{aligned}\]Prefault operating power angle is given by or
During fault no power is transferred \(P_{eII} = 0\)
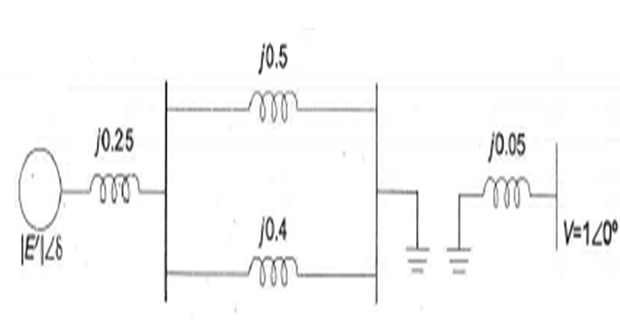
Post fault operation (fault cleared by opening the faulted line)

- \[\delta_{\max }=\pi-\sin ^{-1} \frac{1}{1.5}=2.41 \text { radians }\]is given by for The maximum permissible angle
- \[\begin{aligned} A_{1} &=P_{m}\left(\delta_{c r}-\delta_{0}\right) \\ &=1.0\left(\delta_{c r}-0.45\right)=\delta_{\mathrm{cr}}-0.45 \\ A_{2} &=\int_{\delta_{0}}^{\delta_{\mathrm{ma}}}\left(P_{e \mathrm{III}}-P_{m}\right) \mathrm{d} \delta \\ &=\int_{\delta}^{2.41}(1.5 \sin \delta-1) \mathrm{d} \delta \\ &=-1.5 \cos \delta-\left.\delta\right|_{\delta_{c}} ^{2.41} \\ &=-1.5\left(\cos 2.41-\cos \delta_{c r}\right)-\left(2.41-\delta_{c r}\right) \\ &=1.5 \cos \delta_{c r}+\delta_{c r}-1.293 \end{aligned}\]Applying equal area criterion for critical clearing angle
- \[\begin{aligned} \delta_{c r}-0.45 &=1.5 \cos \delta_{c r}+\delta_{c r}-1.293 \\ \cos \delta_{c r} &=0.843 / 1.5=0.562 \end{aligned}\]\[\delta_{c r}=55.8^{\circ}\]and solving or Setting