Short Transmission Lines

Demonstrative Video

Problem-1

A \(1\phi\) overhead transmission line delivers 1100 kW at 33 kV at 0·8 p.f. lagging. The total resistance and inductive reactance of the line are 10 \(\Omega\) and 15 \(\Omega\) respectively.

Determine :

sending end voltage
sending end power factor and
transmission efficiency.

Solution-1

Load power factor, \(\cos \phi_{R}=0.8\) lagging
Total line impedance, \(\vec{Z}=R+j X_{L}=10+j 15\)
Receiving end voltage, \(V_{R}=33 \mathrm{kV}=33,000 \mathrm{V}\)
\[\text{As} \quad \cos \phi_{R}=0 \cdot 8 \quad \therefore \quad \sin \phi_{R}=0.6\]
Line current,

\[\begin{aligned} \overrightarrow{V_{R}} &=V_{R}+j 0=33000 \mathrm{V} \\ \vec{I} &=I\left(\cos \phi_{R}-j \sin \phi_{R}\right) \\ &=41 \cdot 67(0-8-j 0 \cdot 6)=33 \cdot 33-j 25 \end{aligned}\]

as the reference phasor, Taking receiving end voltage

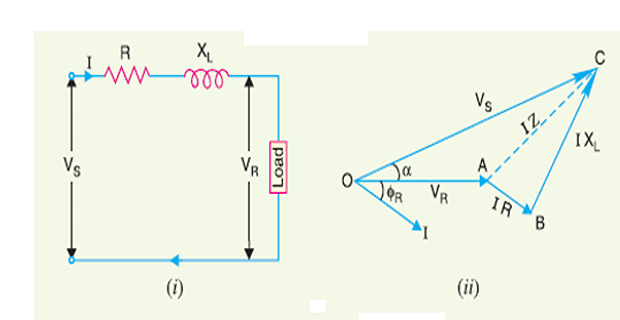
\[\begin{array}{l} =33,000+(33 \cdot 33-j 25-0)(10+j 15) \\ =33,000+333 \cdot 3-j 250+j 500+375 \\ =33,708 \cdot 3+j 250 \end{array}\]
\(V_{S}=\sqrt{(33,708 \cdot 3)^{2}+(250)^{2}}=33,709 \mathrm{V}\)\(\therefore\) Sending end voltage,
\[\alpha=\tan ^{-1} \frac{250}{33,708 \cdot 3}=\tan ^{-1} 0 \cdot 0074=0 \cdot 42^{\circ}\]
is and Angle between
\[\phi_{S}=\phi_{R}+\alpha=36 \cdot 87^{\circ}+0.42^{\circ}=37 \cdot 29^{\circ}\]
Sending end power factor angle is
Sending end p.f., \(\cos \phi_{S}=\cos 37 \cdot 29^{\circ}=0 \cdot 7956\) lagging

\(\text { Line losses }=I^{2} R=(41 \cdot 67)^{2} \times 10=17,364 \mathrm{W}=17.364 \mathrm{kW}\)
\(\text { Output delivered } =1100 \mathrm{kW}\)
\(\text { Power sent } =1100+17 \cdot 364=1117 \cdot 364 \mathrm{kW}\)
\[=\dfrac{\text { Power delivered }}{\text { Power sent }} \times 100=\frac{1100}{1117 \cdot 364} \times 100=98 \cdot 44 \%\]
Transmission efficiency
\[\begin{aligned} V_{S} &=V_{R}+I R \cos \phi_{R}+I X_{L} \sin \phi_{R}(\text { approximately }) \\ &=33,000+41 \cdot 67 \times 10 \times 0.8+41 \cdot 67 \times 15 \times 0.6 \\ &=33,000+333 \cdot 36+375 \cdot 03 \\ &=33708 \cdot 39 \mathrm{V} \text{which is approx. the same as above} \end{aligned}\]
\[\begin{aligned} \cos \phi_{\mathrm{S}} &=\frac{V_{R} \cos \phi_{R}+I R}{V_{S}}=\frac{33,000 \times 0 \cdot 8+41 \cdot 67 \times 10}{33,708 \cdot 39}\\ &=\frac{26,816 \cdot 7}{33,708 \cdot 39} =0.7958 \end{aligned}\]
can also be calculated as follows: and Note.

Problem-2

What is the maximum length in km for a 1-phase transmission line having copper conductor of 0·775 cm\(^2\) cross-section over which 200 kW at unity power factor and at 3300V are to be delivered ? The efficiency of transmission is 90%. Take specific resistance as 1.725 \(\mu \Omega\) cm.

Solution-2

\(\text { Receiving end power }=200 \mathrm{kW}=2,00,000 \mathrm{W}\)
Transmission efficiency \(=0.9\)
Sending end power \(=\dfrac{2,00,000}{0.9}=2,22,222 \mathrm{W}\)
Line losses \(=2,22,222-2,00,000=22,222 \mathrm{W}\)
Line current, \(I=\dfrac{200 \times 10^{3}}{3,300 \times 1}=60 \cdot 6 \mathrm{A}\)
Line losses \(=2 I^{2} R\) \(\left(R = \text{resistance/conductor}\right)\)

\[\begin{aligned} \Rightarrow 22,222&=2(60 \cdot 6)^{2} \times R\\ R & =\dfrac{22,222}{2 \times(60 \cdot 6)^{2}}=3 \cdot 025 \Omega \end{aligned}\]
length \(l=\dfrac{R a}{\rho}=\dfrac{3 \cdot 025 \times 0 \cdot 775}{1 \cdot 725 \times 10^{-6}}=1 \cdot 36 \times 10^{6} \mathrm{cm}=13 \cdot 6 \mathrm{km}\)

Problem-3

An overhead 3-phase transmission line delivers 5000 kW at 22 kV at 0·8 p.f. lagging. The resistance and reactance of each conductor is 4 \(\Omega\) and 6 \(\Omega\) respectively. Determine :

sending end voltage
percentage regulation
transmission efficiency

Solution-3

Load power factor \(\cos \phi_{R}=0.8\) lagging
Receiving end voltage/phase \(V_{R}=22,000 / \sqrt{3}=12,700 \mathrm{V}\)
Impedance/phase \(\vec{Z}=4+j 6\)

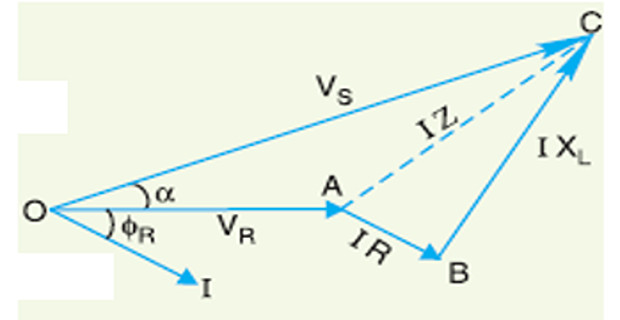
Line current \(I=\dfrac{5000 \times 10^{3}}{3 \times 12700 \times 0 \cdot 8}=164 \mathrm{A}\)
\(\cos \phi_{R}=0 \cdot 8 \quad \therefore \sin \phi_{R}=0 \cdot 6\)

\[\begin{aligned} \overrightarrow{V_{R}} &=V_{R}+j 0=12700 \mathrm{V} \\ \vec{I} &=I\left(\cos \phi_{R}-j \sin \phi_{R}\right)=164(0 \cdot 8-j 0 \cdot 6)=131 \cdot 2-j 98 \cdot 4 \end{aligned}\]

as the reference phasor, Taking

\[\begin{aligned} \overrightarrow{V_{S}} &=\overrightarrow{V_{R}}+\vec{I} \vec{Z}\\ &=12700+(131 \cdot 2-j 98 \cdot 4)(4+j 6) \\ &=12700+524 \cdot 8+j 787 \cdot 2-j 393 \cdot 6+590 \cdot 4 \\ &=13815 \cdot 2+j 393 \cdot 6 \\ \text { Magnitude of } V_{S} &=\sqrt{(13815 \cdot 2)^{2}+(393 \cdot 6)^{2}}=13820 \cdot 8 \mathrm{V} \end{aligned}\]
Sending end voltage per phase is
Line value of \(V_{S}=\sqrt{3} \times 13820 \cdot 8=23938 \mathrm{V}=23 \cdot 938 \mathrm{kV}\)
\[=\dfrac{V_{S}-V_{R}}{V_{R}} \times 100=\dfrac{13820 \cdot 8-12700}{12700} \times 100=8 \cdot 825 \%\]
\(\%\)
Line losses \(=3 I^{2} R=3 \times(164)^{2} \times 4=3,22,752 \mathrm{W}=322.752 \mathrm{kW}\)
Transmission efficiency \(=\dfrac{5000}{5000+322 \cdot 752} \times 100=93 \cdot 94 \%\)

Problem-4

Estimate the distance over which a load of 15000 kW at a p.f. 0·8 lagging can be delivered by a 3-phase transmission line having conductors each of resistance 1 \(\Omega\) per kilometre. The voltage at the receiving end is to be 132 kV and the loss in the transmission is to be 5%.

Solution-4

Line current,

\[\begin{aligned} I&=\frac{\text { Power delivered }}{\sqrt{3} \times \text { line voltage } \times \text { power factor }}\\ &=\frac{15000 \times 10^{3}}{\sqrt{3} \times 132 \times 10^{3} \times 0.8}=82 \mathrm{A} \end{aligned}\]
Line losses \(=5 \%\) of power delivered \(=0.05 \times 15000=750 \mathrm{kW}\)
\[\begin{aligned} \text { Line losses } &=3 I^{2} R \\ 750 \times 10^{3} &=3 \times(82)^{2} \times R\\ \rightarrow R&=\frac{750 \times 10^{3}}{3 \times(82)^{2}}=37 \cdot 18 \Omega \end{aligned}\]
Resistance of each conductor per \(\mathrm{km}\) is \(1 \Omega\) (given).
Length of line \(=37 \cdot 18 \mathrm{km}\)