Per-Unit Quantities
Demonstrative Video
Revision of Important Formulas
Problem-1
A three-phase generator with rating 1000 kVA, 33 kV has its armature resistance and synchronous reactance as 20 \(\Omega\)/phase and 70 \(\Omega\)/phase. Calculate p.u. impedance of the generator.
Solution-1
The generator ratings are chosen as base \(\mathrm{kV}\) and base \(\mathrm{kVA}\).
Base kilovolt, \(\mathrm{kV}_{\mathrm{b}}=33 \mathrm{kV}\)
Base kilovoltampere, \(\mathrm{kVA}_{\mathrm{b}}=1000 \mathrm{kVA}\)
- \[Z_{b}=\frac{\left(k V_{b}\right)^{2}}{M V A_{b}}=\frac{(33)^{2}}{1000 / 1000}=1089 \Omega\]Base impedance
- \[\mathrm{Z}=(20+\mathrm{j} 70) \Omega / phase\]Actual impedance per phase
- \[Z_{\mathrm{pu}}=\frac{\text { Actual impedance }}{\text { Base impedance }}=\frac{Z}{Z_{b}}=\frac{20+j 70}{1089}=0.018+j 0.064 \mathrm{p} . \mathrm{u}\]p.u. impedance
Problem-2
A three phase, \(\Delta\) -Y transformer with rating \(100 \mathrm{kVA}, 11 \mathrm{kV} / 400 \mathrm{~V}\) has its primary and secondary leakage reactance as \(12 \Omega /\) phase and \(0.05 \Omega /\) phase respectively. Calculate the p.u. reactance of transformer.
Solution-2
Case-1: HV winding (primary) rating chosen as base value
Base kilovolt, \(\mathrm{kV}_{\mathrm{b}}=11 \mathrm{kV}\)
Base kilo volt-ampere, \(\mathrm{kVA}_{\mathrm{b}}=100 \mathrm{kVA}\)
- \[\mathrm{Z}_{\mathrm{b}}=\frac{\left(\mathrm{kV}_{\mathrm{b}}\right)^{2}}{\mathrm{MVA}_{\mathrm{b}}}=\frac{(11)^{2}}{100 / 1000}=1210 \Omega\]Base impedance per phase
Transformer line voltage ratio, \(\mathrm{K}=\dfrac{400}{11,000}=0.0364\)
- \[\begin{aligned} \mathrm{X}_{01}&=\mathrm{X}_{1}+\mathrm{X}_{2}^{*}\\ &=\mathrm{X}_{1}+\frac{\mathrm{X}_{2}}{\mathrm{~K}^{2}}\\ &=12+\frac{0.05}{(0.0364)^{2}}=12+37.737 = 49.737 \Omega / \text { phase } \end{aligned}\]Total leakage reactance referred to primary
- \[\begin{aligned} & X_{p u}=\frac{\text { Total leakage reactance }}{\text { Base impedance }}\\ &=\frac{X_{01}}{Z_{b}}=\frac{49.737}{1210}=0.0411 \mathrm{p.u} \end{aligned}\]p. u. reactance per phase
Case-2: LV winding (secondary) rating chosen as base value
Base kilovolt, \(\mathrm{kV}_{\mathrm{b}}=400 / 1000=0.4 \mathrm{kV}\)
Base kilovoltampere, \(\mathrm{kVA}_{\mathrm{b}}=100 \mathrm{kVA}\)
- \[\mathrm{Z}_{\mathrm{b}}=\frac{\left(\mathrm{kV}_{\mathrm{b}}\right)^{2}}{\mathrm{MVA}_{\mathrm{b}}}=\frac{(0.4)^{2}}{100 / 1000}=1.6 \Omega\]Base impedance per phase
Transformer line voltage ratio, \(\mathrm{K}=\dfrac{400}{11,000}=0.0364\)
- \[\begin{aligned} \mathrm{X}_{02}&=\mathrm{X}_{1}^{\prime}+\mathrm{X}_{2}=\mathrm{K}^{2} \mathrm{X}_{1}+\mathrm{X}_{2}\\ &=(0.0364)^{2} \times 12+0.05\\ &=0.0159+0.05=0.0659 \Omega / \text { phase } \end{aligned}\]Total leakage reactance referred to secondary
p.u. reactance per phase, \(\mathrm{X}_{\mathrm{pu}}=\dfrac{\text { Total leakage reactance }}{\text { Base impedance }}=\dfrac{\mathrm{X}_{02}}{\mathrm{Z}_{\mathrm{b}}}=\dfrac{0.0659}{1.6}=0.0411 \mathrm{p}\).u.
Note:
It is observed that the p.u. reactance of a transformer referred to primary and secondary are same.
In \(3\phi\) transformer of the voltage ratio K is obtained using line values then using this value of K the phase impedance per phase of star-side can be directly transferred to delta side or vice versa
Problem-3
Using the P.U. system and taking into account the transformer percent impedances, solve for the current in each part of the three-phase system shown below. assume both transformers are either delta-delta or wye-wye connected and that there is no phase shift between primary and secondary current and voltage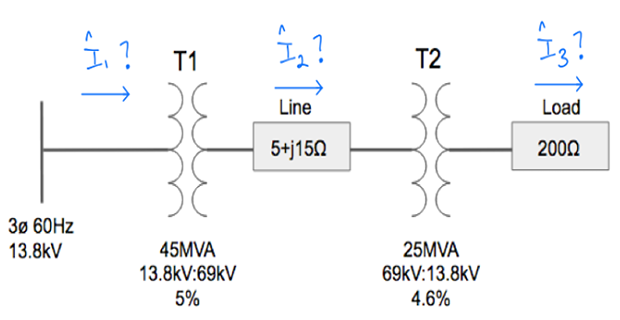
Solution-3
Step-1: Separate by Voltage zones
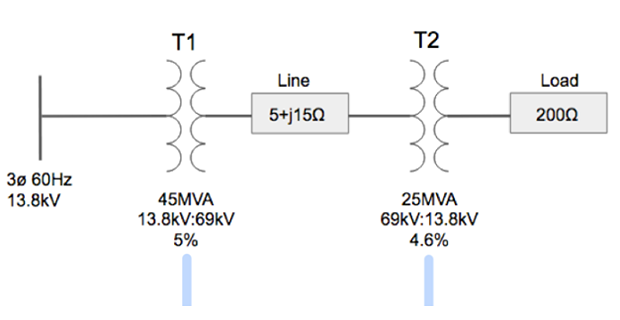
Step-2: Assign base values
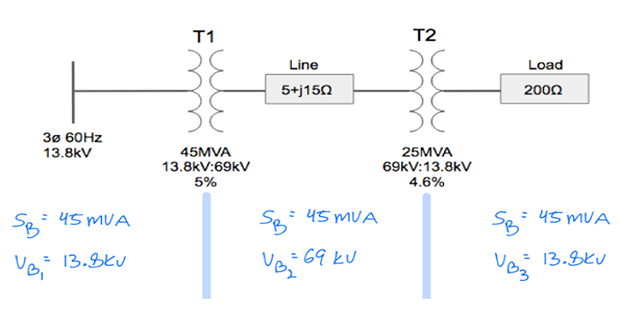
Step-3: Calculate \(Z_B\) for each zones
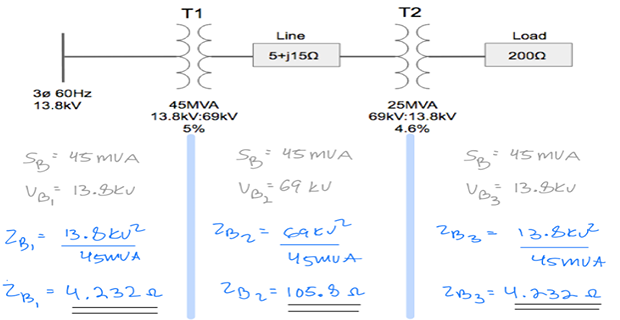
Step-4: Calculate \(Z_{p.u.}\) for each zone
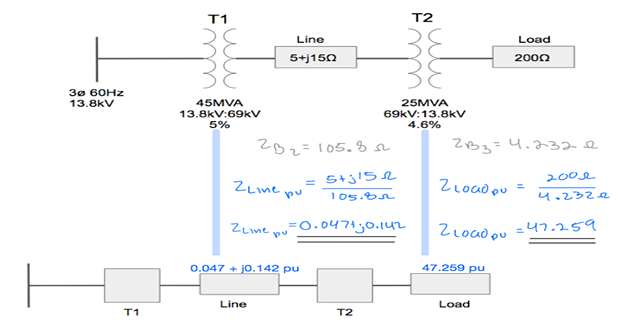
Step-5: Calculate \(Z_{p.u}\) for Tran-1
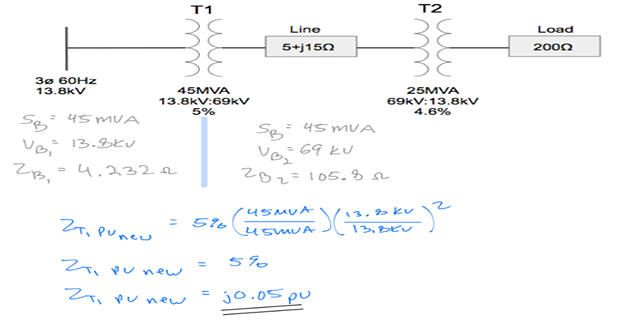
Step-6: Calculate \(Z_{p.u}\) for Tran-2
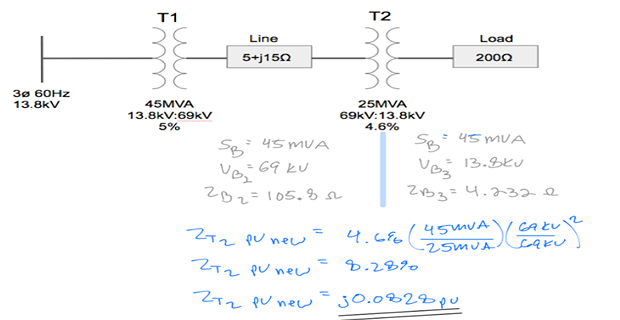
Step-7: Calculate p.u. current and voltages
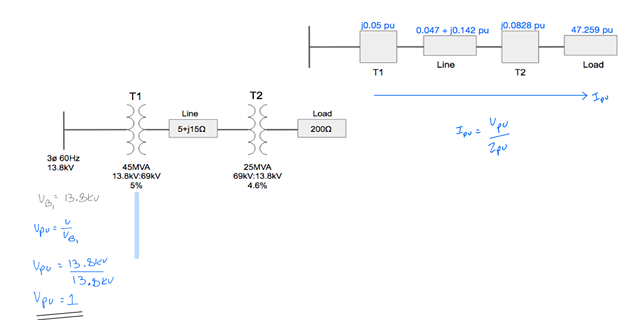
Step-8: Use Ohm’s Law to calculate p.u. current
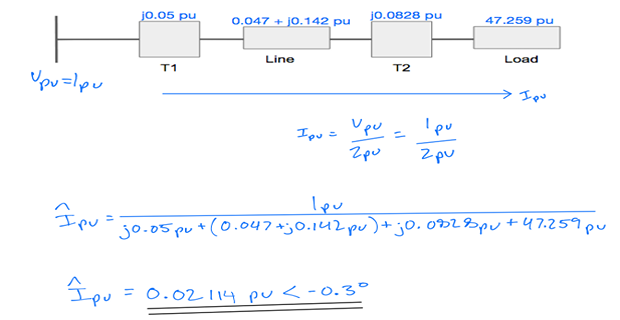
Step-9: Calculate \(I_B\) in each zone
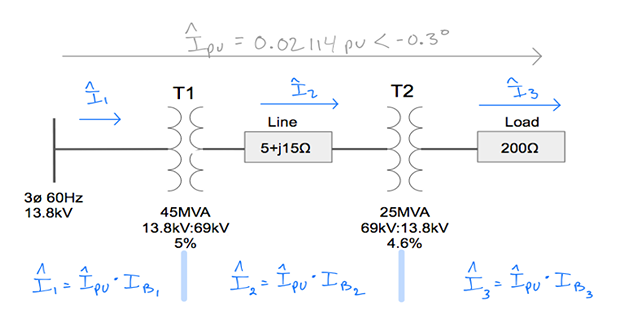
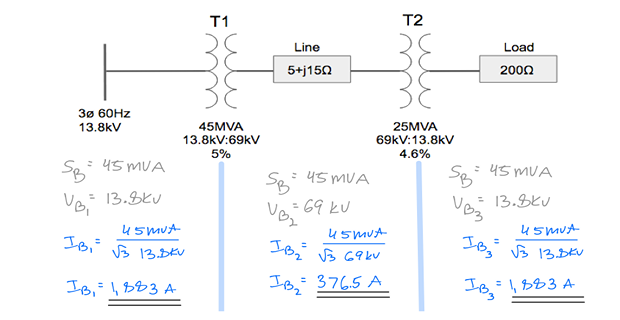
Step-10: Calculate actual current in each zone
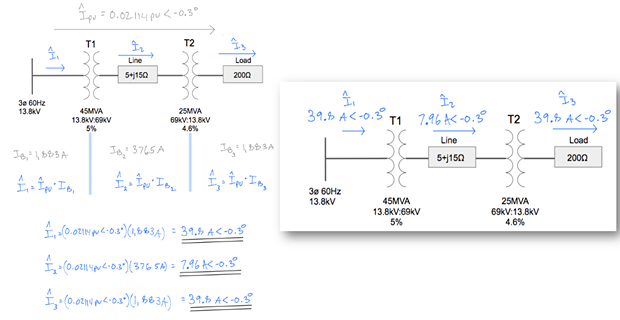
Step-11: Check using T/F ratios