Demonstrative Video
Tutorial-2: Load Characteristics and utlization
Terms Associated With Plant Utilization
\(=\dfrac{\mbox{average load}}{\mbox{maximum (peak) load}} < 1\)
\(=\dfrac{\mbox{maximum load in a given time period}}{\mbox{maximum possible load }}\)
\(=\dfrac{\mbox{Sum of individual maximum demands}}{\mbox{maximum load on the system }}\)
\(=\dfrac{\mbox{Actual energy produced}}{\mbox{maximum possible that could be produced }}\)
\(=\dfrac{\mbox{Actual energy produced (KWh)}}{\mbox{plant capacity (KW) $\times$ Time (in hrs) of operation }}\)
Problem-1:
The maximum demand on a power station is \(100 \mathrm{MW}\). If the annual load factor is \(40 \%\), calculate the total energy generated in a year.
Solution-1
Problem-2:
A generating station has a connected load of \(43 \mathrm{MW}\) and a maximum demand of \(20 \mathrm{MW} ;\) the units generated being \(61.5 \times 10^{6}\) per anmum. Calculate the following:
the demand factor and
load factor:
Solution-2
Demand factor \(=\dfrac{\text { Max. demand }}{\text { Connected load }}=\frac{20}{43}=0 \cdot 465\)
Average demand \(=\dfrac{\text { Units generated / annum }}{\text { Hours in a year }}=\frac{61 \cdot 5 \times 10^{6}}{8760}=7020 \mathrm{kW}\)
Load factor \(=\dfrac{\text { Average demand }}{\text { Max. demand }}=\dfrac{7020}{20 \times 10^{3}}=0.351\) or \(35 \cdot 1 \%\)
Problem-3:
A \(100 \mathrm{MW}\) power station delivers
\(100 \mathrm{MW}\) for 2 hours
\(50 \mathrm{MW}\) for 6 hours
is shut down for the rest of each day
It is also shut down for maintenance for 45 days each year
Calculate its annual load factor:
Solution-3
- \[=(100 \times 2)+(50 \times 6)=500 \mathrm{MWh}\]Energy supplied for each working day
Station operates for \(=365-45=320\) days in a year
Energy supplied/year \(=500 \times 320=160,000 \mathrm{MWh}\)
- \[\begin{aligned} &=\frac{\text { MWh supplied per annum }}{\text { Max. demand in MW } \times \text { Working hours }} \times 100 \\ &=\frac{160,000}{(100) \times(320 \times 24)} \times 100=20 \cdot 8 \% \end{aligned}\]Annual load factor
Problem-4:
A generating station has a maximum demand of \(25 \mathrm{MW}\), a load factor of \(60 \%\), plant capacity factor of \(50 \%\) and plant use factor of \(72 \%\).
Find
the reserve capacity of the plant
the daily energy produced and
maximum energy that could be produced daily if the plant while running as per schedule, were fully loaded.
Solution-4
Load factor \(=\frac{\text { Average demand }}{\text { Maximum demand }}\)
\[\begin{aligned} 0 \cdot 60 & =\frac{\text { Average demand }}{25} \\ \Rightarrow \text{Average demand} & =25 \times 0.60=15 \mathrm{MW} \end{aligned}\]Plant capacity factor \(=\frac{\text { Average demand }}{\text { Plant capacity }}\)
\[\begin{aligned} \Rightarrow \text{ Plant capacity}& =\frac{\text { Average demand }}{\text { Plant capacity factor }}=\frac{15}{0 \cdot 5}=30 \mathrm{MW} \end{aligned}\]- \[=30-25=5 \mathrm{MW}\]Plant capacity - maximum demand Reserve capacity of plant
Daily energy produced
\[\begin{aligned} & = \text{Average demand} \times 24 \\ & =15 \times 24=360 \mathrm{MWh} \end{aligned}\]Maximum energy that could be produced
\[\begin{aligned} & =\frac{\text { Actual energy produced in a day }}{\text { Plant use factor }} \\ & =\frac{360}{0.72}=500 ~ \mathrm{MWh} / \mathrm{day} \end{aligned}\]
Problem-5:
A diesel station supplies the following loads to various consumers:
If the maximum demand on the station is \(2500 ~\mathrm{kW}\) and the number of \(\mathrm{kWh}\) generated per year is \(45 \times 10^{5},\) determine
the diversity factor
annual load factor
Solution-5
Diversity factor \(=\dfrac{1500+750+100+450}{2500}=1 \cdot 12\)
Average demand \(=\dfrac{\text { kWh generated } / \text { annum }}{\text { Hours in a year }}=\dfrac{45 \times 10^{5}}{ 8760}=513 \cdot 7 \mathrm{kW}\)
Load factor \(=\dfrac{\text { Average load }}{\text { Max. demand }}=\dfrac{513 \cdot 7}{2500}=0 \cdot 205=20 \cdot 5 \%\)
Problem-6:
A power station has
a maximum demand of \(15000 \mathrm{kW}\)
The annual load factor is 50%
plant capacity factor is 40%.
Determine the reserve capacity of the plant.
Solution-6
- \[\begin{aligned} &=\text { Max. demand } \times \text { L.F. } \times \text { Hours in a year } \\ &=(15000) \times(0.5) \times(8760) \mathrm{kWh} \\ &=65.7 \times 10^{6} \mathrm{kWh} \end{aligned}\]Energy generated/annum
- \[\begin{aligned} \Rightarrow \text{Plant capacity} &=\frac{65 \cdot 7 \times 10^{6}}{0 \cdot 4 \times 8760}=18,750 \mathrm{kW} \end{aligned}\]Plant capacity factor
- \[\begin{aligned} &=\text { Plant capacity - Max. demand } \\ &=18,750-15000=3750 \mathrm{kW} \end{aligned}\]Reserve capacity
Problem-7:
A power supply is having the following loads :
If the overall system diversity factor is \(1 \cdot 35,\) determine
maximum demand
connected load of each type.
Solution-7
The sum of maximum demands of three types of loads is \(=1500+2000+10,000=13,500\) kW.
As the system diversity factor is 1.35 , \(\Rightarrow\) Max. demand on supply system \(=13,500 / 1 \cdot 35=10,000 \mathrm{kW}\)
- \[=1500 \times 1 \cdot 2=1800 \mathrm{kW}\]diversity factor Max. domestic demand Each type of load has its own diversity factor among its consumers. Sum of max. demands of different domestic consumers
Connected domestic load \(=1800 / 0 \cdot 8=2250 \mathrm{kW}\)
Connected commercial load \(=2000 \times 1 \cdot 1 / 0 \cdot 9=2444 \mathrm{kW}\)
Connected industrial load \(=10,000 \times 1 \cdot 25 / 1=12,500 \mathrm{kW}\)
Problem-8:
At the end of a power distribution system, a certain feeder supplies three distribution transformers, each one supplying a group of customers whose connected loads are as under:
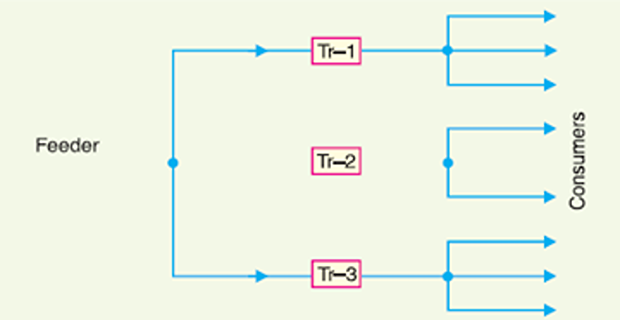
If the diversity factor among the transformers is \(1 \cdot 3,\) find the maximum load on the feeder.
Solution-8
- \[=\text { connected load } \times \text { demand factor }=10 \times 0.65=6.5 \mathrm{kW}\]Sum of max. demands of customers on Transformer 1
- \[\therefore \quad \text { Maximum demand on Transformer } 1=6.5 / 1 \cdot 5=4 \cdot 33 \mathrm{kW}\], As the diversity factor among consumers connected to transformer No. 1 is
Maximum demand on Transformer \(2=12 \times 0.6 / 3 \cdot 5=2.057 \mathrm{kW}\)
Maximum demand on Transformer \(3=15 \times 0.7 / 1 \cdot 5=7 \mathrm{kW}\)
As the diversity factor among transformers is \(1 \cdot 3\),
\[\text{Maximum demand on feeder}=\frac{4 \cdot 33+2 \cdot 057+7}{1 \cdot 3}=10 \cdot 3 \mathrm{kW}\]
Problem-9:
It has been desired to install a diesel power station to supply power in a suburban area having the following particulars:
1000 houses with average connected load of \(1 \cdot 5 \mathrm{kW}\) in each house. The demand factor and diversity factor being 0.4 and 2.5 respectively.
10 factories having overall maximum demand of \(90 \mathrm{kW}\).
7 tubewells of \(7 \mathrm{kW}\) each and operating together in the morning. The diversity factor among above three types of consumers is 1 - \(2 .\)
What should be the minimum capacity of power station ?
Solution-9
Sum of max. demands of houses \(=(1 \cdot 5 \times 0 \cdot 4) \times 1000=600 \mathrm{kW}\)
Max. demand for domestic load \(=600 / 2 \cdot 5=240 \mathrm{kW}\)
Max. demand for factories \(=90 \mathrm{kW}\)
Max. demand for tubewells \(=7^{*} \times 7=49 \mathrm{kW}\)
The sum of maximum demands of three types of loads is \(=240+90+49=379 \mathrm{kW}\). As the diversity factor among the three types of loads is \(1 \cdot 2\),
Max. demand on station \(=379 / 1 \cdot 2=316 \mathrm{kW}\)
Minimum capacity of station requried \(=316 \mathrm{kW}\)
Problem-10:
A generating station has the following daily load cycle :
Draw the load curve and find
maximum demand
units generated per day
average load
load factor:
Solution-10
Daily curve is drawn by taking the load along \(Y\) -axis and time along \(X\) -axis. For the given load cycle, the load curve is shown
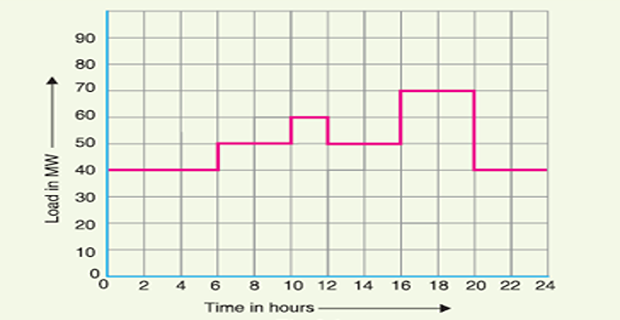
Units generated/day \(=\) Area (in \(\mathrm{kWh}\) ) under the load curve
\(\begin{aligned} &=10^{3}[40 \times 6+50 \times 4+60 \times 2+50 \times 4+70 \times 4+40 \times 4] \\ &=10^{3}[240+200+120+200+280+160] \mathrm{kWh} \\ &=12 \times 10^{5} ~\mathrm{kWh} \end{aligned}\)
Average load \(=\dfrac{\text { Units generated / day }}{24 \text { hours }}=\dfrac{12 \times 10^{5}}{24}=50,000~ \mathrm{kW}\)
Load factor \(=\dfrac{\text { Average load }}{\text { Max. demand }}=\dfrac{50.000}{70 \times 10^{3}}=0.714=71.4 \%\)