Solved Problems on Complex Power and Inductance Calculation of Transmission Lines

Demonstrative Video

Problem-1

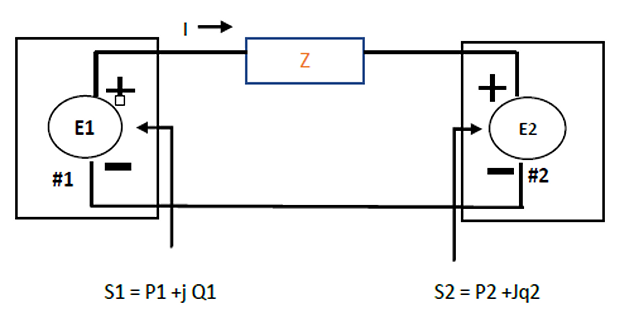
  • Two ideal voltage sources designated as machines 1 and 2 are connected, as shown in fig. If \(E_1= 100\angle 0^\circ ~ V, E_2=100\angle30^\circ~ V ~\text{and}~ Z=0+j5\) ohms, determine

    1. whether each machine is generating or consuming real power and the amount

    2. whether each machine is receiving or supplying reactive power and the amount , and

    3. the P and Q absorbed by the impedance.

image

Solution-1

\[\begin{aligned} &I=\frac{E_1-E_2}{Z}=\frac{100+j 0-(86.6+j50)}{j5} \mathrm{~S} \\ &=\frac{13.4-j50}{j 5} =-10-\mathrm{j} 2.68= 10.35 \angle 195^{\circ}\\ &\mathrm{S}_1=\mathrm{E}_1(-I)^{*} =\mathrm{P}_1+\mathrm{jQ}_1 \\ &=100(10+\mathrm{j} 2.68)^{*} =1000-\mathrm{j} 268 \mathrm{VA} \\ &\mathrm{S}_2=\mathrm{E}_2(I)^{*} =\mathrm{P}_2+\mathrm{jQ}_2 \\ &=(86.6+\mathrm{j} 50)(-10+\mathrm{j} 2.68) \\ &=-1000-\mathrm{j} 268 \mathrm{VA} \end{aligned}\]

  • Machine 1 may be expected to be a generator because of the current direction and polarity markings. However , since P1 is positive and Q1 is negative, the machine consumes energy at the rate of 1000W and supplies reactive power of 268 VAR. the machine is actually a motor.

  • Machine 2, expected to be a motor, has negative P2 and negative Q2. Therefore, this machine generates energy at the rate of 1000W and supplies reactive power of 268 VAR. the machine is actually a generator.

  • Note that the supplied reactive power of 268+268= 536 VAR , which is required by the inductive reactance of 5ohm. Since the impedance is purely reactive, no P is consumed by the impedance, and all the watts generated by machine 2 are transferred to machine 1 .

\[\begin{aligned} &=I^{2} . X \\ &=\left(10.35^{2}\right) .5 \\ &=536 \mathrm{VAR} \end{aligned}\]
The reactive power absorbed in the series impedance is

Problem-2

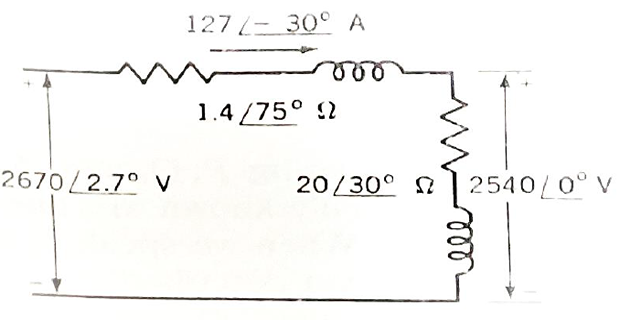
  • The terminal voltage of Y- connected load consisting of three equal impedances of \(20\angle 30^\circ\) ohms is 4.4 KV line to line. The impedance of each of three lines connecting the load to a bus at a sub station is \(Z_L= 1.4\angle 75^{\circ}\). Find the line-line voltage at the substation bus.

Solution-2

  • \[\begin{gathered} =\frac{4400}{\sqrt{3}} =2540 \mathrm{~V} \end{gathered}\]
    The magnitude of the voltage to the neutral at the load is
  • \[\begin{aligned} &I_{an}=\frac{2540 \angle 0 ^{\circ}}{20 \angle 30 ^{\circ}} =127.0 \angle-30^{\circ} \end{aligned}\]
    and , the voltage across the load, is chosen as reference If
  • \[\begin{aligned} & V_{an}+\left(I_{an} . Z_{\mathrm{L}}\right)\\ &=2540 \angle 0^{\circ}+\left(127 \angle-30^{\circ} .14 \angle 75^{\circ}\right)\\ &=2540 \angle 0^{0}+177.8 \angle 45^{0}=2670 \angle 2.70^{\circ} \end{aligned}\]
    The line to neutral voltage at the substation is

  • the magnitude of the voltage at the substation bus is \(=\sqrt{3} * 2.67=4.62 \mathrm{KV}\)

image

Problem-3

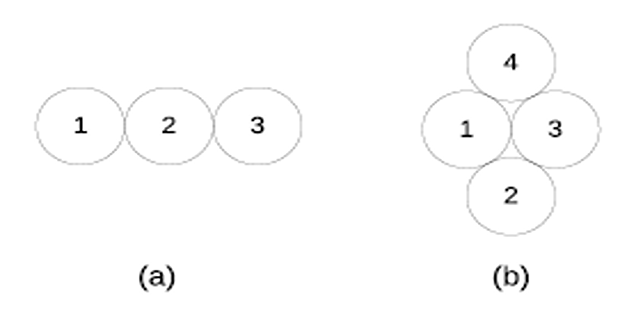
  • Find the self GMD for each conductor configuration shown in Figure. Radius of each conductor is 1 cm.
    image

Solution-3

\[\begin{gathered} G M R=\sqrt[3]{G M R_{1} \times G M R_{2} \times G M R_{3}} \\ G M R_{1}=G M R_{3}=\sqrt[3]{0.7788 r \times 2 r \times 4 r}=1.84 r=0.0184 \\ G M R_{2}=\sqrt[3]{0.7788 r \times 2 r \times 2 r}=1.4604 r=0.014604 \\ G M R=\sqrt[3]{1.84 r \times 1.4604 r \times 1.84 r}=1.7036 r=0.017036 \end{gathered}\]
(b)
image

Problem-4

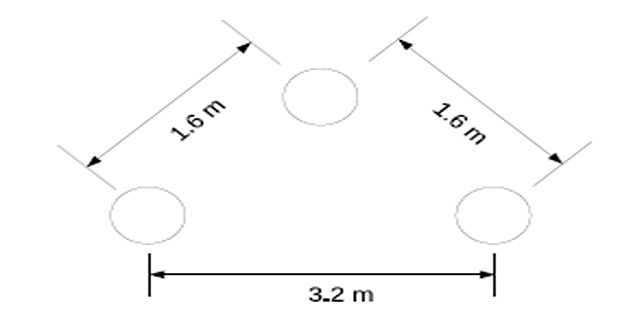
  • Determine the inductance of a 3 phase line operating at 50 Hz and conductors arranged as given in figure. The conductor diameter is 0.8 cm.
    image

Solution-4

\[\begin{gathered} G M R=0.7788 \times 0.004=0.0031152 \mathrm{~m} \\ G M D=\sqrt[6]{(1.6 \times 1.6)(1.6 \times 3.2)(1.6 \times 3.2)}=2.0158 \mathrm{~m} \\ L=2 \times 10^{-7} \ln \frac{2.0158}{0.0031152}=1.294 \mathrm{mH} / \mathrm{km} \end{gathered}\]
image

Problem-5

  • A 500KV line has a bundling arrangement of two conductors per phase as shown in fig. Compute the reactance per phase of this line at 50Hz. Each conductor carries 50% of the phase current . Assume full transposition.
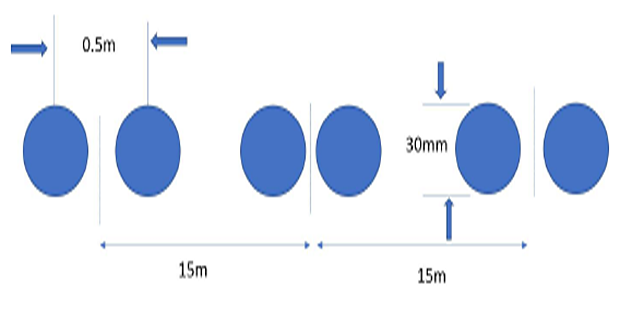
    image

Solution-5

\[\begin{aligned} D_{a b} &=D_{b c}=[d(d+s)(d-s) d]^{1 / 4} \\ &=(15 \times 15.5 \times 14.5 \times 15)^{1 / 4}=15 \mathrm{~m} \\ D_{c a} &=[2 d(2 d+s)(2 d-s) 2 d]^{1 / 4} \\ &=(30 \times 30.5 \times 29.5 \times 30)^{1 / 4}=30 \mathrm{~m} \\ D_{e q} &=(15 \times 15 \times 30)^{1 / 3}=18.89 \mathrm{~m} \\ D_{s} &=\left(r^{\prime} s r^{\prime} s\right)^{1 / 4}=\left(r^{\prime} s\right)^{1 / 2} \\ &=(0.7788 \times 0.015 \times 0.5)^{1 / 2} =0.0764 \mathrm{~m} \end{aligned}\]
\(d=15 \mathrm{~m}, s=0.5 \mathrm{~m}\)
image
\[\begin{aligned} X_{L} &=314 \times 0.461 \times 10^{-3} \log \dfrac{18.89}{0.0764} \\ &=\mathbf{0 . 3 4 6} \Omega / \mathbf{k m} \end{aligned}\]
Inductive reactance/phase

Problem-6

  • A double circuit three phase line is shown in fig .The conductors a,a’;b,b’; c,c’ belong to the same phase respectively.The radius of each conductor is 1.5cm. Find the inductance of the double-circuit line in mH/km/phase.
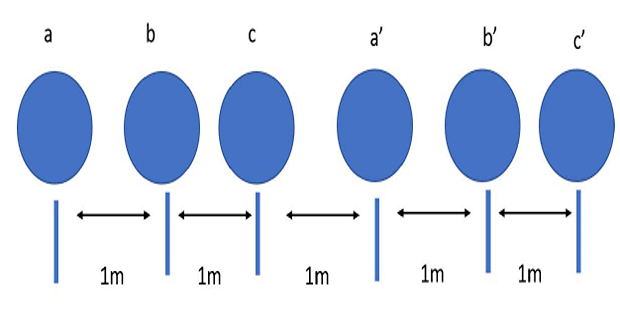
    image

Solution-6

\[\begin{gathered} r^{\prime}=0.7788 \times 1.5 \times 10^{-2}=0.0117 \mathrm{~m} \\ D_{a b}=\left(1^{*} 4^{*} 1^{*} 2\right)^{1 / 4} ; \mathrm{Dbc}=\left(1^{*} 4^{*} 1^{*} 2\right)^{1 / 4} ; \mathrm{D}_{c a}=(2 * 1 * 2 * 5)^{1 / 4} \\ D_{m}=\sqrt[3]{D_{a b} D_{b c} D_{c a}}=\sqrt[12]{1280}=1.815 \mathrm{~m} \\ D_{s a}=D_{s b}=D_{s c}=\sqrt{0.0117 \times 3}=0.187 \\ D_{s}=0.187 \mathrm{~m} \\ L = 0.461 \cdot \log \dfrac{1.815}{0.187} = 0.455 ~\text{mH/km/phase} \end{gathered}\]
image

Problem-7

  • Calculate the 50Hz inductive reactance at 1m spacing in ohms/km of a cable consisting of 12 equal strands around a non conducting core. The diameter of each strand is 0.25cm and the outside diameter of the cable is 1.25cm.
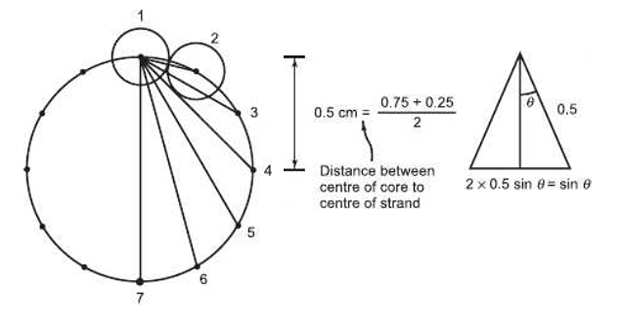
    image

Solution-7

\[\begin{aligned} D_{12} &=\sin 15^{\circ}=0.259 \mathrm{~cm} \qquad D_{13}=\sin 30^{\circ} =0.5 \mathrm{~cm} \\ D_{14} &=\sin 45^{\circ}=0.707 \mathrm{~cm} \qquad D_{15}=\sin 60^{\circ}=0.866 \mathrm{~cm} \\ D_{16} &=\sin 75^{\circ}=0.965 \mathrm{~cm} \qquad D_{17}=\sin 90^{\circ}=1.0 \mathrm{~cm} \\ D_{11} &=r^{\prime}=(0.25 / 2) \times 0.7788=0.097 \mathrm{~cm} \end{aligned}\]
\(=1.25-2 \times(0.25)=0.75 \mathrm{~cm}\)
image
\[\begin{aligned} D_{s}&=\left\{(0.097 \times 1) \times(0.259)^{2} \times(0.5)^{2} \times(0.707)^{2} \times(0.866)^{2} \times(0.965)^{2}\right\}^{1 / 12}\\ &=0.536 \mathrm{~cm} \\ D_{m} & \approx 1 \mathrm{~m} \\ L &=2 \times 0.461 \log \frac{100}{0.536}=2.094 \mathrm{mH} / \mathrm{km} \\ X &=314 \times 2.094 \times 10^{-3}=0.658 \Omega / \mathrm{km} \end{aligned}\]
image