Admittance Bus Solved Problems

Demonstrative Video

Revision of Important Concept

The bus admittance matrix can be formed by inspection using the following guidelines.

The diagonal element \(Y_{i j}\) is given by sum of all the admittances connected to node-j.
The off-diagonal element \(Y_{j k}\) is given by negative of the sum of all the admittances connected between node-j and node-k.

Problem-1

For the network shown in the Figure,

Form the bus admittance matrix
Determine the reduced admittance matrix by eliminating node-4

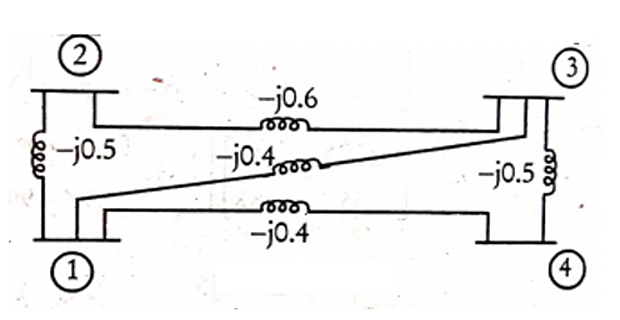
All values are marked in p.u.

Solution-1

\[ \mathbf{Y}_{\text {bus }}=\left[\begin{array}{cccc} -(\mathrm{j} 0.5+\mathrm{j} 0.4+\mathrm{j} 0.4) & \mathrm{j} 0.5 & \mathrm{j} 0.4 & \mathrm{j} 0.4 \\ \mathrm{j} 0.5 & -(\mathrm{j} 0.5+\mathrm{j} 0.6) & \mathrm{j} 0.6 & 0 \\ \mathrm{j} 0.4 & \mathrm{j} 0.6 & -(\mathrm{j} 0.6+\mathrm{j} 0.5+\mathrm{j} 0.4) & \mathrm{j} 0.5 \\ \mathrm{j} 0.4 & 0 & \mathrm{j} 0.5 & -(\mathrm{j} 0.5+\mathrm{j} 0.4) \end{array}\right] \]

\[\mathbf{Y}_{\text {bus }}=\left[\begin{array}{cccc} -\mathrm{j} 1.3 & \mathrm{j} 0.5 & \mathrm{j} 0.4 & \mathrm{j} 0.4 \\ \mathrm{j} 0.5 & -\mathrm{j} 1.1 & \mathrm{j} 0.6 & 0 \\ \mathrm{j} 0.4 & \mathrm{j} 0.6 & -\mathrm{j} 1.5 & \mathrm{j} 0.5 \\ \mathrm{j} 0.4 & 0 & \mathrm{j} 0.5 & -\mathrm{j} 0.9 \end{array}\right]\]

\[Y_{j k, n c w}=Y_{j k} \cdots \frac{Y_{j n} Y_{n k}}{Y_{n n}} ; \text { where } n=4 ; j=1,2,3 \text { and } k=1,2,3\]
column is given by row and The elements of new bus admittance matrix after eliminating the
The bus admittance matrix is symmetrical, \(\therefore Y_{k j, n e w}=Y_{j k, \text { new }}\)

\(\mathrm{Y}_{11, \text { new }}=\mathrm{Y}_{11}-\frac{\mathrm{Y}_{14} \mathrm{Y}_{41}}{\mathrm{Y}_{44}}=-\mathrm{j} 1.3-\frac{(\mathrm{j} 0.4)(\mathrm{j} 0.4)}{-\mathrm{j} 0.9}=-\mathrm{j} 1.12\)
\(\mathrm{Y}_{12, \mathrm{new}}=\mathrm{Y}_{12}-\frac{\mathrm{Y}_{14} \mathrm{Y}_{42}}{\mathrm{Y}_{44}}=\mathrm{j} 0.5-\frac{(\mathrm{j} 0.4 \times 0)}{-\mathrm{j} 0.9}=\mathrm{j} 0.5\)
\(\mathrm{Y}_{13, \mathrm{ncw}}=\mathrm{Y}_{13}-\frac{\mathrm{Y}_{14} \mathrm{Y}_{43}}{\mathrm{Y}_{44}}=\mathrm{j} 0.4-\frac{(\mathrm{j} 0.4)(\mathrm{j} 0.5)}{-\mathrm{j} 0.9}=\mathrm{j} 0.622\)
\(\mathrm{Y}_{21, \mathrm{new}}=\mathrm{Y}_{12, \text { new }}=\mathrm{j} 0.5\)
\(\mathrm{Y}_{22, \text { new }}=\mathrm{Y}_{22}-\frac{\mathrm{Y}_{24} \mathrm{Y}_{42}}{\mathrm{Y}_{44}}=-\mathrm{j} 1.1-\frac{(0)(0)}{-\mathrm{j} 0.9}=-\mathrm{j} 1.1\)
\(\mathrm{Y}_{23, \mathrm{new}}=\mathrm{Y}_{23}-\frac{\mathrm{Y}_{24} \mathrm{Y}_{43}}{\mathrm{Y}_{44}}=\mathrm{j} 0.6-\frac{(0)(\mathrm{j} 0.5)}{-\mathrm{j} 0.9}=\mathrm{j} 0.6\)
\(\mathrm{Y}_{31, \mathrm{new}}=\mathrm{Y}_{13, \mathrm{new}}=\mathrm{j} 0.622\)
\(\mathrm{Y}_{32, \mathrm{new}}=\mathrm{Y}_{23, \mathrm{new}}=\mathrm{j} 0.6\)
\(\mathrm{Y}_{33, \mathrm{new}}=\mathrm{Y}_{33}-\frac{\mathrm{Y}_{34} \mathrm{Y}_{43}}{\mathrm{Y}_{44}}=-\mathrm{j} 1.5-\frac{(\mathrm{j} 0.5)(\mathrm{j} 0.5)}{-\mathrm{j} 0.9}=-\mathrm{j} 1.222\)

\[\mathbf{Y}_{\text {bus }}=\left[\begin{array}{ccc} -\mathrm{j} 1.12 & \mathrm{j} 0.5 & \mathrm{j} 0.622 \\ \mathrm{j} 0.5 & -\mathrm{j} 1.1 & \mathrm{j} 0.6 \\ \mathrm{j} 0.622 & \mathrm{j} 0.6 & -\mathrm{j} 1.222 \end{array}\right]\]

row is shown below. The reduced bus admittance matrix after eliminating

Problem-2

Determine the bus admittance matrix of the system whose reactance diagram is shown in Fig. the currents and admittances are given in p.u.
Determine the reduced bus admittance matrix after eliminating node-3.

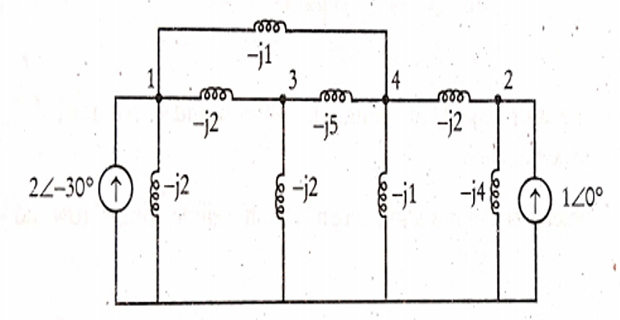
Solution-2

\[Y_{\text {bus }}=\left[\begin{array}{rrrr} -\mathrm{j} 2-\mathrm{j} 2-\mathrm{jl} & .0 & \mathrm{j} 2 & \mathrm{j} 1 \\ 0 & -\mathrm{j} 2-\mathrm{j} 4 & 0 & \mathrm{j} 2 \\ \mathrm{j} 2 & 0 & -\mathrm{j} 2-\mathrm{j} 2-\mathrm{j} 5 & \mathrm{j} 5 \\ \mathrm{j} 1 & \mathrm{j} 2 & \mathrm{j} 5 & -\mathrm{j} 1-\mathrm{j} 5-\mathrm{j} 2-\mathrm{j} 1 \end{array}\right]\]

For eliminating node- 3 , \(Y_{bus}\) is rearranged by interchanging row-3 & row-4, and then interchanging column.3 & column - 4 .
\[\mathbf{Y}_{\text {bus }}=\left[\begin{array}{rrrr} -\mathrm{j} 5 & 0 & \mathrm{j} 2 & \mathrm{j} 1 \\ 0 & -\mathrm{j} 6 & 0 & \mathrm{j} 2 \\ \mathrm{j} 1 & \mathrm{j} 2 & \mathrm{j} 5 & -\mathrm{j} 9 \\ \mathrm{j} 2 & 0 & -\mathrm{j} 9 & \mathrm{j} 5 \end{array}\right]\]
matrix we get, row -4 of After interchanging row
\[\mathbf{Y}_{\text {bus }}=\left[\begin{array}{cccc} -\mathrm{j} 5 & 0 & \mathrm{j} 1 & \mathrm{j} 2 \\ 0 & -\mathrm{j} 6 & \mathrm{j} 2 & 0 \\ \mathrm{j} 1 & \mathrm{j} 2 & -\mathrm{j} 9 & \mathrm{j} 5 \\ \mathrm{j} 2 & 0 & \mathrm{j} 5 & -\mathrm{j} 9 \end{array}\right]\]
matrix we get, column -4 of After interchanging column

Now the last row & last column [i.e., \(4^{\text {th }}\) row and \(4^{\text {th }}\) column \(]\) of \(\mathrm{Y}_{\text {bus }}\) matrix can be eliminated.
The elements of \(Y_{bus,new}\) after eliminating \(4^{\text {th }}\) row and \(4^{\text {th }}\) column is given by

\[Y_{j k, n e w}=Y_{j k}-\frac{Y_{j n} Y_{n k}}{Y_{n n}} \text { where } n=4 ; j=1,2,3 \text { and } k=1,2,3\]

\(Y_{11, \text { new }}=Y_{11}-\dfrac{Y_{14} Y_{41}}{Y_{44}}=-j 5-\frac{(j 2)(j 2)}{-j 9}=-j 4.556\)
\(Y_{12, new}=Y_{12}-\dfrac{Y_{14} Y_{42}}{Y_{44}}=0-\frac{j 2 \times 0}{-j 9}=0\)
\(Y_{13, new}=Y_{13}-\dfrac{Y_{14} Y_{43}}{Y_{44}}=j 1-\frac{(j 2)(j 5)}{-j 9}=j 2.111\)
\(Y_{21, new}=Y_{12, \text { new }}=0\)
\(Y_{22 . \text { new }}=Y_{22}-\dfrac{Y_{24} Y_{42}}{Y_{44}}=-j 6-\frac{0 \times 0}{-j 9}=-j 6\)
\(Y_{23, new}=Y_{23}-\dfrac{Y_{24} Y_{43}}{Y_{44}}=j 2-\dfrac{0 \times j 5}{-j 9}=j 2\)
\(Y_{31, \text { new }}=Y_{13, new}=j 2.111\)
\(Y_{32, new}=Y_{23, \text { new }}=j 2\)
\(Y_{33, \text { new }}=Y_{33}-\dfrac{Y_{34} Y_{43}}{Y_{44}}=-j 9-\frac{j 5 \times j 5}{-j 9}=-j 6.222\)

\[\mathbf{Y}_{\text {bus }}=\left[\begin{array}{ccc} -\mathrm{j} 4.556 & 0 & \mathrm{j} 2.111 \\ 0 & -\mathrm{j} 6 & \mathrm{j} 2 \\ \mathrm{j} 2.111 & \mathrm{j} 2 & -\mathrm{j} 6.222 \end{array}\right]\]

The reduced bus admittance matrix after eliminating bus- 3 is given by,