Demonstrative Video
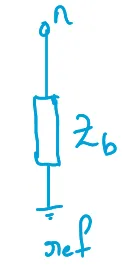
Revision of Algorithm
\[Z_{\text{Bus}} = \left[Z_b\right]\]
\[\left[
\begin{array}{c|c}
Z_{\text{old}} & Z_k^c \\
\hline
Z_k^r & Z_{kk}+Z_b
\end{array}
\right]\]
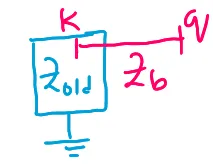
\[Z_{\text{new}} =
\left[Z_{\text{old}}\right]-\dfrac{1}{Z_{kk}+Z_b}\left[Z_k^c\right]\left[Z_k^r\right]\]
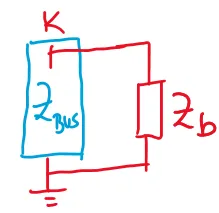
\[\begin{aligned}
Z_{\text{new}} & =
\left[Z_{\text{old}}\right]-\dfrac{1}{Z_{ll}}\left[Z_{j-k}^c\right]
\left[Z_{j-k}^r\right]\\
Z_{ll} & = Z_{kk}+Z_{jj}+Z_b-2Z_{jk}
\end{aligned}\]
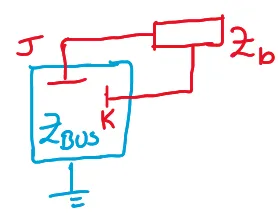
Problem-1
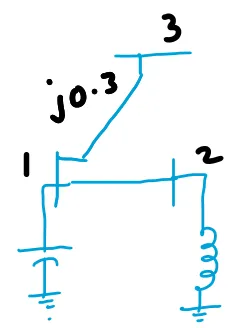
Form the Z-BUS
matrix for the following figure using step by step method.
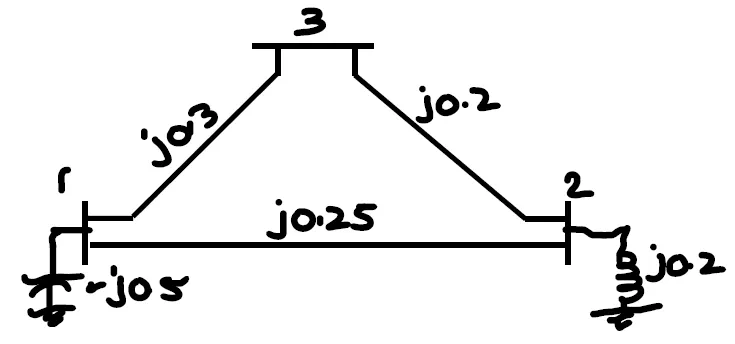
Solution-1
\[Z_{\text{Bus}}
= \left[-j0.5\right]\]
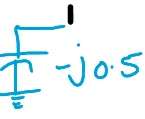
\[\left[
\begin{array}{c|c}
Z_{\text{old}} & Z_k^c \\
\hline
Z_k^r & Z_{kk}+Z_b
\end{array}
\right]\]
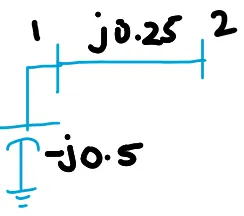
\[Z_{\text{Old}} = \left[\begin{array}{cc}
-j0.5 & -j0.5\\
-j0.5 & -j0.25
\end{array}
\right]\]
\[
\begin{aligned}
Z_{\text {new }} &=\left[Z_{\text {old
}}\right]-\frac{1}{Z_{b}+Z_{k k}}\left[Z_{k}^{c}\right]
\left[Z_{k}^{r}\right] \\
Z_{\text {Bus,new }} &=Z_{\text {old }}-\frac{1}{-j
0.75+j 0.2}\left[\begin{array}{c}
-j 0.5 \\
-j 0.25
\end{array}\right][-j 0.5-j 0.25] \\
Z_{\text {Bus,new }} &=\left[\begin{array}{cc}
j 4.5 & j 2 \\
j 2 & j 1
\end{array}\right]
\end{aligned}
\]
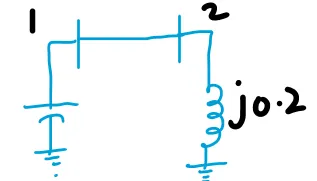
\[\left[
\begin{array}{c|c}
Z_{\text{old}} & Z_k^c \\
\hline
Z_k^r & Z_{kk}+Z_b
\end{array}
\right]\]
\[Z_{\text {Bus }}=\left[\begin{array}{cc|c}
j 4.5 & j 2 & j 4.5 \\
j2 & j1 & j2 \\ \hline
j 4.5 & j 2 & j 4.8
\end{array}\right]\]
Step-5
\[Z_{\text {Old }}=\left[\begin{array}{cc|c}
j 4.5 & j 2 & j 4.5 \\
j2 & j1 & j2 \\ \hline
j 4.5 & j 2 & j 4.8
\end{array}\right]\]
\[\begin{aligned}
Z_{\text{new}} & =
\left[Z_{\text{old}}\right]-\dfrac{1}{Z_{ll}}\left[Z_{j-k}^c\right]
\left[Z_{j-k}^r\right]\\
Z_{ll} & = Z_{kk}+Z_{jj}+Z_b-2Z_{jk}
\end{aligned}\]
\[Z_{\text {BUS
}}=\left[\begin{array}{ccc}
j 1.37 & j 0.75 & j 1.0 \\
j 0.75 & j 0.5 & j 0.6 \\
j 1.0 & j 0.6 & j 0.88
\end{array}\right]\]
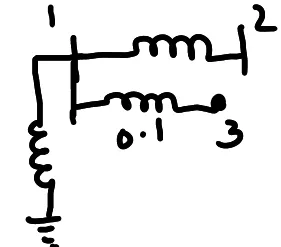
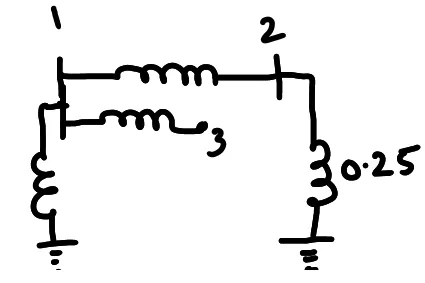
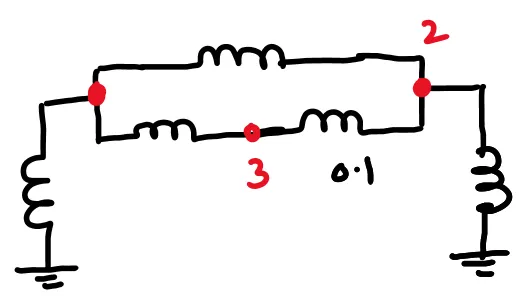
Problem-2
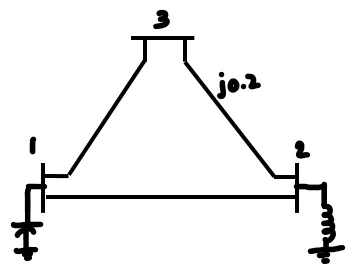
Form the Z-BUS
matrix for the following figure using step by step method.
All the values are in p.u. quantities. 
Solution-2
\[Z_{\text{Bus}}
= \left[0.25\right]\]
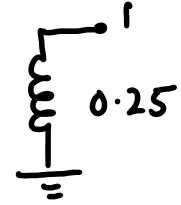
\[\left[
\begin{array}{c|c}
Z_{\text{old}} & Z_k^c \\
\hline
Z_k^r & Z_{kk}+Z_b
\end{array}
\right]\]
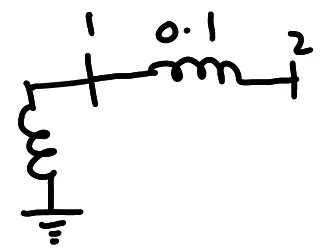
\[\left[
\begin{array}{c|c}
Z_{\text{old}} & Z_k^c \\
\hline
Z_k^r & Z_{kk}+Z_b
\end{array}
\right]\]
\[Z_{\text{new}}
=
\left[Z_{\text{old}}\right]-\dfrac{1}{Z_{kk}+Z_b}\left[Z_k^c\right]\left[Z_k^r\right]\]
\[\begin{aligned}
Z_{\text{new}} & =
\left[Z_{\text{old}}\right]-\dfrac{1}{Z_{ll}}\left[Z_{j-k}^c\right]
\left[Z_{j-k}^r\right]\\
Z_{ll} & = Z_{kk}+Z_{jj}+Z_b-2Z_{jk}
\end{aligned}\]
\[\begin{aligned}
&\left[\begin{array}{lll}
0.1456 & 0.1048 & 0.1458 \\
0.1042 & 0.1458 & 0.1042 \\
0.1458 & 0.1042 & 0.2958
\end{array}\right]-\frac{1}{0.1+0.1458+2.458-2(0.1408)} \times
\\
&\left[\begin{array}{c}
-0.0416 \\
0.0417 \\
0.1416
\end{array}\right]\left[\begin{array}{lll}
-0.0416 & 0.0417 & -0.1416
\end{array}\right]\\
&=\left[\begin{array}{lll}
0.1397 & 0.1103 & 0.1250 \\
0.1103 & 0.1397 & 0.1250 \\
0.1250 & 0.1250 & 0.1750
\end{array}\right]
\end{aligned}\]
MATLAB CODE
clear all;
clc
disp('------Formulation Z-bus Matrix-------')
n=input('enter total number of busses including Ref busses = ');
zbus=zeros(n,n);
t=1;
while t==1;
zbus
s=menu('specify case no','new bus to reference bus','existing bus to new bus',...
'between existing busses','existing bus to reference bus','print','quit');
switch s
case{1} % new bus to reference bus
zb=input('enter impedance value = ');
zbus=zb;
case{2} % existing bus to new bus
k=input('enter starting bus number = ');
n=input('enter new bus number = ');
zb=input('Enter impedance value = ');
for i=1:n
if i==n
zbus(n,n)=zbus(k,k)+zb;
else
zbus(i,n)=zbus(i,k);
zbus(n,i)=zbus(k,i);
end
end
case{3} % between existing busse
a=input('enter first bus number = ');
b=input('enter second bus number = ');
zb=input('enter impedance value = ');
m1=zb+zbus(a,a)+zbus(b,b)-(2*zbus(a,b));
ztemp=(1/m1)*((zbus(:,a))-(zbus(:,b)))*((zbus(a,:))-(zbus(b,:)));
zbus=zbus-ztemp;
case{4} % existing bus to reference bu
k=input('enter the old bus no = ');
zb=input('enter the impedance value = ');
m2=zbus(k,k)+zb;
ztemp=(1/m2)*zbus(:,k)*zbus(k,:);
zbus=zbus-ztemp;
case{5}
zbus
case{6}
'end program'
t=0;
end
end