Sequence Impedances and Networks in Power Systems

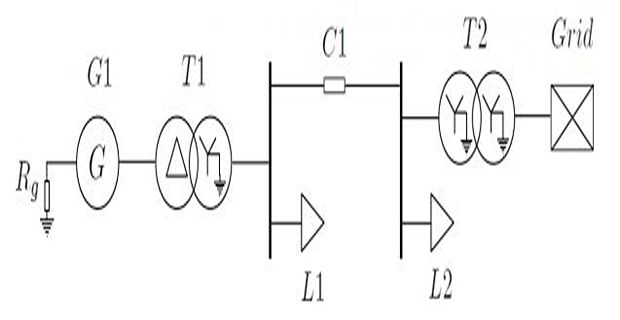
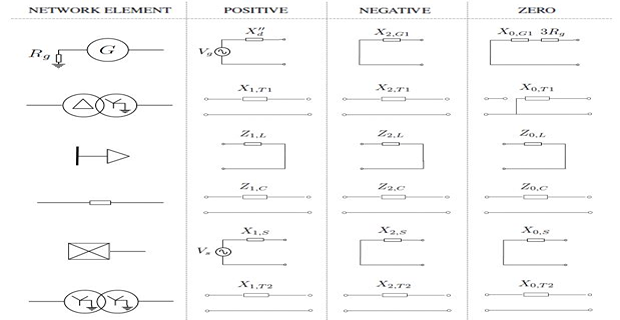
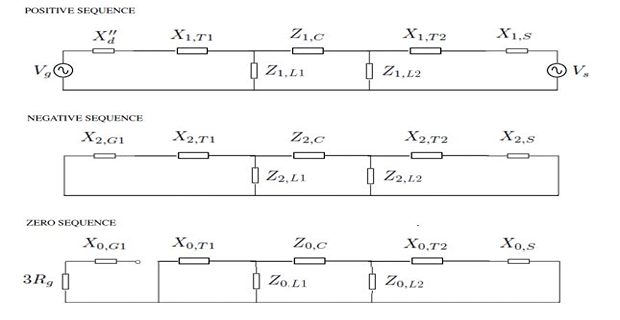
Demonstrative Video

Sequence Impedance & Sequence Networks

Sequence impedances are impedances offered by the power system components to positive, negative, and zero sequence currents.
- positive sequence current $\rightarrow$ positive sequence impedance
- negative sequence current $\rightarrow$ negative sequence impedance
- zero sequence current $\rightarrow$ zero sequence impedance
$\mathrm{V_{drop}}$ caused by current of a certain sequence depends on the impedance of the element to that sequence current.
Impedance or reactance diagram formed using the impedances of any one sequence only is called sequence network for that particular sequence.
- positive sequence impedance $\rightarrow$ positive sequence network
- negative sequence impedance $\rightarrow$ negative sequence network
- zero sequence impedance $\rightarrow$ zero sequence network

Sequence Circuits for Loads

$$\begin{align*} I_{n} & =I_{a}+I_{b}+I_{c}\\ & =3I_{a0}+\underset{0}{\underbrace{\left(I_{a1}+I_{b1}+I_{c1}\right)}+}\underset{0}{\underbrace{\left(I_{a2}+I_{b2}+I_{c2}\right)}}\\ & =3I_{a0} \end{align*}$$

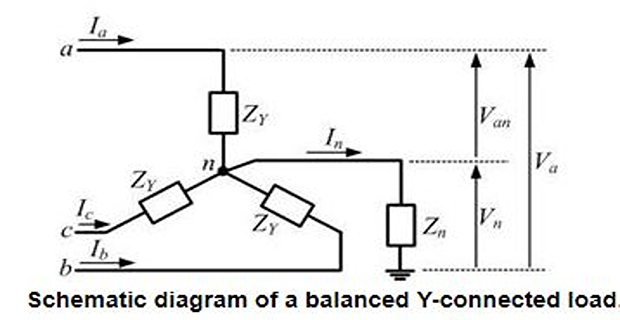
There will not be any positive or negative sequence current flowing out of the neutral point.
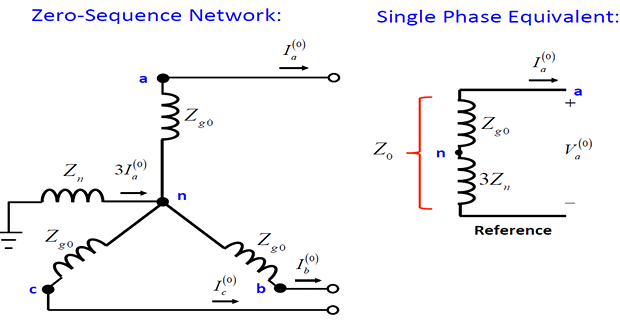
\[V_{n}=3Z_{n}I_{a0}\]
The voltage drop between the neutral and ground is

\[\begin{aligned} V_{a}&=V_{an}+V_{n}\\ &=V_{an}+3Z_{n}I_{a0} \end{aligned}\]

Now

\[\left[\begin{array}{c} V_{a}\\ V_{b}\\ V_{c} \end{array}\right]=\left[\begin{array}{c} V_{an}\\ V_{bn}\\ V_{cn} \end{array}\right]+\left[\begin{array}{c} V_{n}\\ V_{n}\\ V_{n} \end{array}\right]=Z_{Y}\left[\begin{array}{c} I_{a}\\ I_{b}\\ I_{c} \end{array}\right]+3Z_{n}I_{a0}\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right]\]

\[\begin{aligned} V_{a012} & =Z_{Y}I_{a012}+3Z_{n}I_{a0}C\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right]\\ \Rightarrow\left[\begin{array}{c} V_{a0}\\ V_{a1}\\ V_{a2} \end{array}\right] & =Z_{Y}\left[\begin{array}{c} I_{a0}\\ I_{a1}\\ I_{a2} \end{array}\right]+3Z_{n}\left[\begin{array}{c} I_{a0}\\ 0\\ 0 \end{array}\right] \end{aligned}\]

$C$We can therefore write similar expression for the other two phases

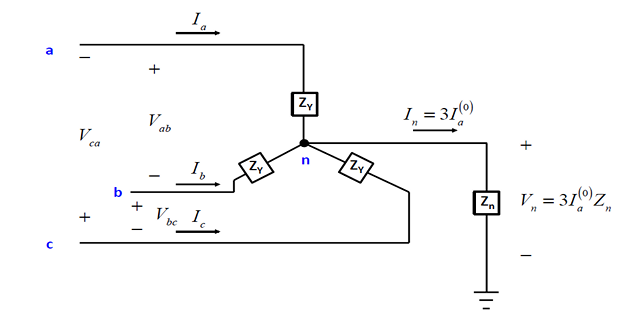
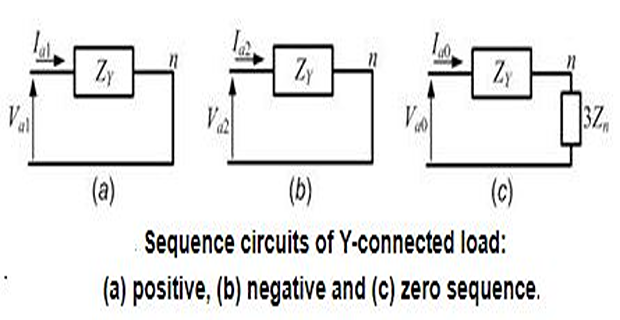
We then find that the zero, positive and negative sequence voltages only depend on their respective sequence component currents.
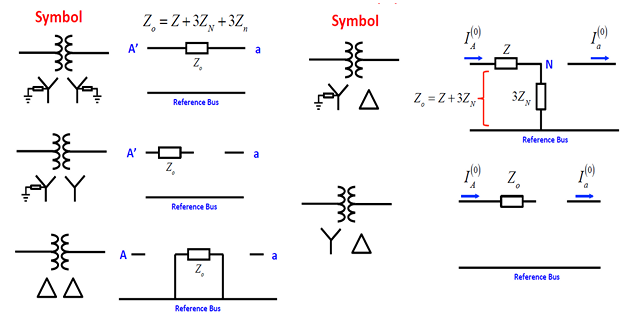
\[Z_{0}=Z_{Y}+3Z_{n}\]
, the zero sequence impedance is equal to While the positive and negative sequence impedances are both equal to
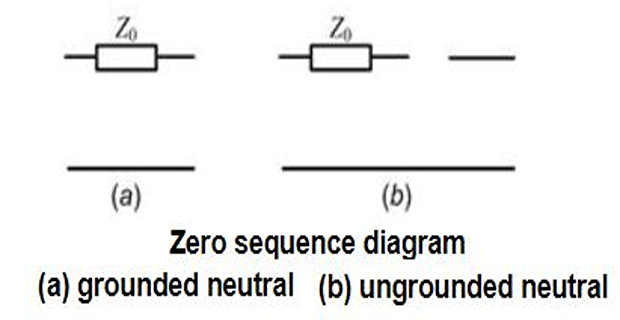
If the neutral is grounded directly (i.e., $Z_n = 0$), then $Z_0 = Z_Y$.
If the neutral is kept floating (i.e., $Z_n = \infty$ ), then there will not be any zero sequence current flowing in the circuit at all.

\[\left. \begin{array}{cc} V_{ab} & =Z_{\varDelta}I_{ab}\\ V_{bc} & =Z_{\varDelta}I_{bc}\\ V_{ca} & =Z_{\varDelta}I_{ca} \end{array}\right\} V_{ab}+V_{bc}+V_{ca}=Z_{\varDelta}\left(I_{ab}+I_{bc}+I_{ca}\right)\]

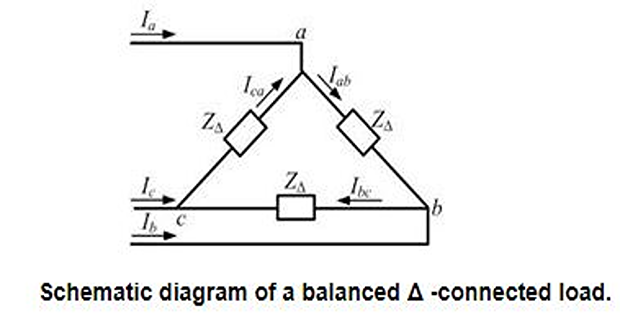
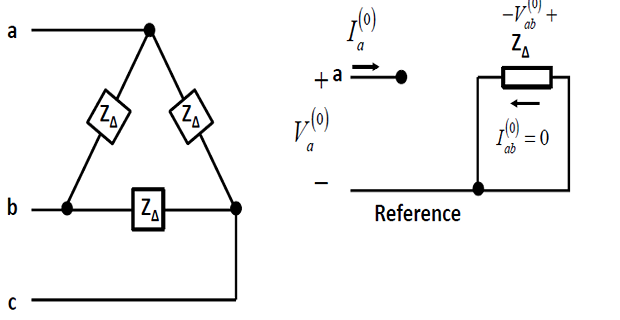
No zero sequence circulating current for a $\varDelta$-connected load
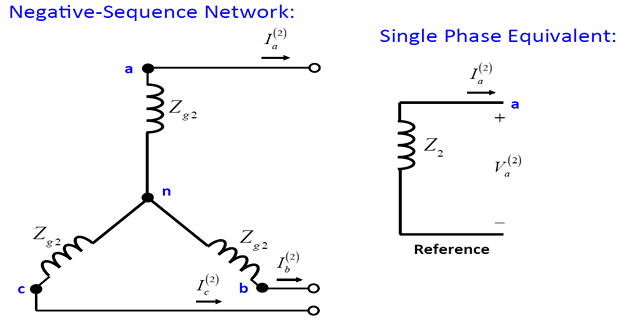
Positive and negative sequence impedance for this load will be equal to $Z_{\varDelta}$.

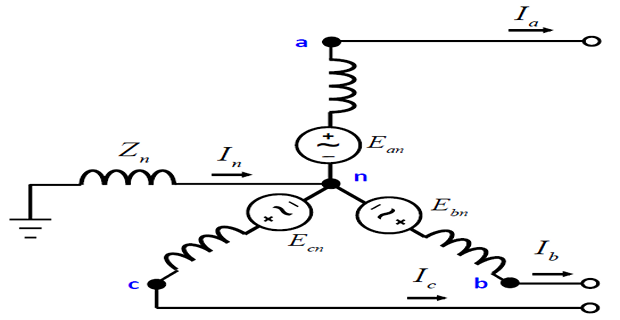
Sequence Circuits for Synchronous Generator

\[I_{n}=I_{a}+I_{b}+I_{c} \neq 0\]

\[\begin{aligned} V_{an} & =-\left(R+j\omega L_{s}\right)I_{a}+j\omega M_{s}\left(I_{b}+I_{c}\right)+E_{an}\\ & =-\left(R+j\omega L_{s}+j\omega M_{s}\right)I_{a}+j\omega M_{s}\left(I_{a}+I_{b}+I_{c}\right)+E_{an} \end{aligned}\]

For phase-a voltage

\[ \left[\begin{array}{c} V_{an}\\ V_{bn}\\ V_{cn} \end{array}\right]=-\left[R+j\omega\left(L_{s}+M_{s}\right)\right]\left[\begin{array}{c} I_{a}\\ I_{b}\\ I_{c} \end{array}\right]+j\omega M_{s}\left[\begin{array}{ccc} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1 \end{array}\right]\left[\begin{array}{c} I_{a}\\ I_{b}\\ I_{c} \end{array}\right]+\left[\begin{array}{c} E_{an}\\ E_{bn}\\ E_{cn} \end{array}\right] \]

Similar expressions can also be written for the other two phases.

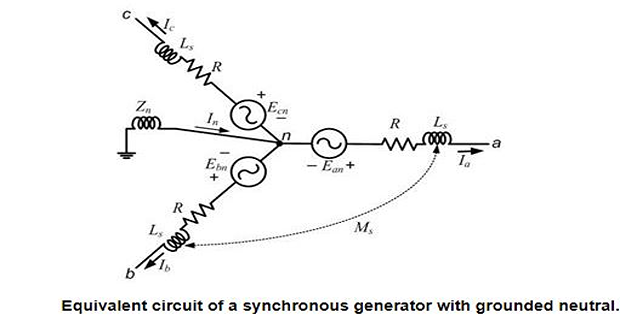
Pre-multiplying both sides by the transformation matrix $C$, we get

\[ \left[\begin{array}{c} V_{an0}\\ V_{an1}\\ V_{an2} \end{array}\right]=-\left[R+j\omega\left(L_{s}+M_{s}\right)\right]\left[\begin{array}{c} I_{a0}\\ I_{a1}\\ I_{a2} \end{array}\right]+j\omega M_{s}C\left[\begin{array}{ccc} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1 \end{array}\right]C^{-1}\left[\begin{array}{c} I_{a0}\\ I_{a1}\\ I_{a2} \end{array}\right]+\left[\begin{array}{c} E_{an0}\\ E_{an1}\\ E_{an2} \end{array}\right] \]

. Therefore Synchronous generator is operated to supply only balanced voltages, we can assume

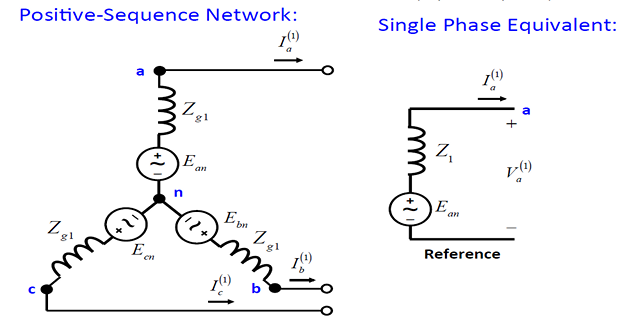
\[\begin{aligned} V_{an0} & =-\left[R+j\omega\left(L_{s}-2M_{s}\right)\right]I_{a0}=-Z_{g0}I_{a0}\\ V_{an1} & =-\left[R+j\omega\left(L_{s}+M_{s}\right)\right]I_{a1}+E_{an}=E_{an}-Z_{1}I_{a1}\\ V_{an2} & =-\left[R+j\omega\left(L_{s}+M_{s}\right)\right]I_{a2}=-Z_{2}I_{a2} \end{aligned}\]
We can separate the terms
For a Y-connected load $V_{a1} = V_{an1}$, $V_{a2} = V_{an2}$ since the neutral current does not affect these voltages.
However $V_{a0} = V_{an0} + V_n$.
Also we know that $V_n = - 3Z_nI_{a0}$.
\[\begin{aligned} V_{a0}&=-\left(Z_{g0}+3Z_{n}\right)I_{a0}\\ &=-Z_{0}I_{a0} \end{aligned}\]
We can therefore rewrite

Sequence Circuits for Transmission Line

\[Z_{aa}=Z_{bb}=Z_{cc}\]

Assuming self impedances of the conductors to be the same, i.e.,

\[\begin{aligned} Z_{ab} & =Z_{bc}=Z_{ca}\\ Z_{an} & =Z_{bn}=Z_{cn} \end{aligned}\]

\[\begin{aligned} V_{an} & =V_{aa'}+V_{a'n'}+V_{n'n}\\ & =V_{aa'}+V_{a'n'}-V_{nn'} \end{aligned}\]

Since the transmission line is assumed to be symmetric, we further assume that the mutual inductances between the conductors are the same and so are the mutual inductances between the conductors and the neutral, i.e.,

\[\begin{aligned} V_{aa'} & =Z_{aa}I_{a}+Z_{ab}\left(I_{b}+I_{c}\right)+Z_{an}I_{n}\\ V_{nn'} & =Z_{nn}I_{a}+Z_{an}\left(I_{a}+I_{b}+I_{c}\right) \end{aligned}\]

\[V_{an}-V_{a^{'}n^{'}}=\left(Z_{aa}-Z_{an}\right)I_{a}+\left(Z_{ab}-Z_{an}\right)\left(I_{b}+I_{c}\right)+\left(Z_{an}-Z_{nn}\right)I_{n}\]

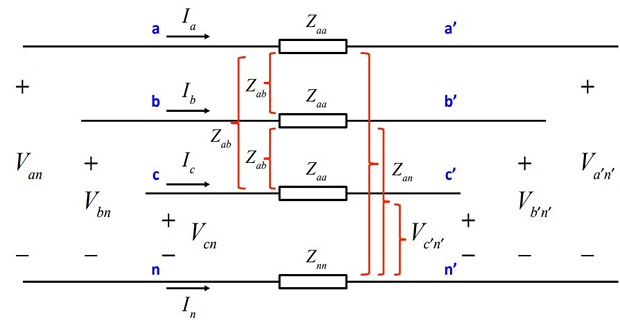
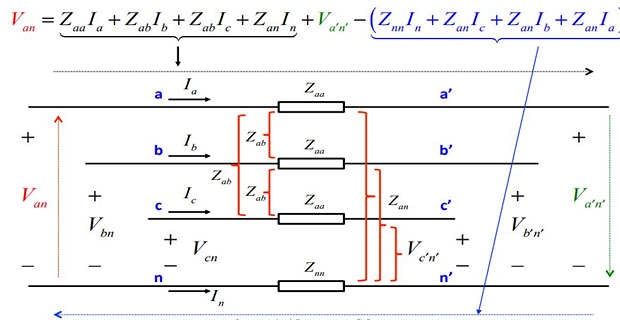
\[I_{n}=-\left(I_{a}+I_{b}+I_{c}\right)\]
Since the neutral provides a return path for the currents
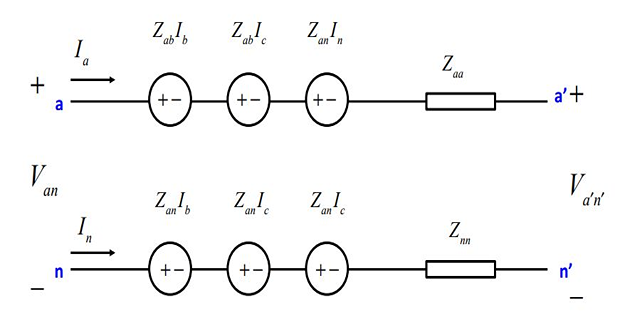
\[\begin{aligned} V_{an}-V_{a^{'}n^{'}} & =\left(Z_{aa}+Z_{nn}-2Z_{an}\right)I_{a}+\left(Z_{ab}+Z_{nn}-2Z_{an}\right)\left(I_{b}+I_{c}\right)\\ \Rightarrow V_{aa^{'}} & =Z_{s}I_{a}+Z_{m}\left(I_{b}+I_{c}\right) \end{aligned}\]
Therefore on substitution , for phase-a of the circuit

\[\begin{aligned} \left[\begin{array}{c} V_{aa^{'}}\\ V_{bb^{'}}\\ V_{cc^{'}} \end{array}\right] & =\left[\begin{array}{ccc} Z_{s} & Z_{m} & Z_{m}\\ Z_{m} & Z_{s} & Z_{m}\\ Z_{m} & Z_{m} & Z_{s} \end{array}\right]\left[\begin{array}{c} I_{a}\\ I_{b}\\ I_{c} \end{array}\right]\\ \Rightarrow V_{aa^{'}012} & =C\left[\begin{array}{ccc} Z_{s} & Z_{m} & Z_{m}\\ Z_{m} & Z_{s} & Z_{m}\\ Z_{m} & Z_{m} & Z_{s} \end{array}\right]C^{-1}I_{a012}\\ \Rightarrow V_{aa^{'}012} & =\dfrac{1}{3}\left[\begin{array}{ccc} 3Z_{s}+6Z_{m} & 0 & 0\\ 0 & 3Z_{s}-3Z_{m} & 0\\ 0 & 0 & 3Z_{s}-3Z_{m} \end{array}\right]I_{a012}\\ \Rightarrow\left[\begin{array}{c} V_{aa^{'}0}\\ V_{aa^{'}1}\\ V_{aa^{'}2} \end{array}\right] & =\left[\begin{array}{ccc} Z_{s}+2Z_{m}\\ & Z_{s}-Z_{m}\\ & & Z_{s}-Z_{m} \end{array}\right]\left[\begin{array}{c} I_{a0}\\ I_{a1}\\ I_{a2} \end{array}\right] \end{aligned}\]

For the other two phases

\[\begin{aligned} Z_{1} & =Z_{2}=Z_{s}-Z_{m}=Z_{aa}-Z_{ab}\\ Z_{0} & =Z_{s}+2Z_{m}=Z_{aa}+2Z_{ab}+3Z_{nn}-6Z_{an} \end{aligned}\]

The sequence equivalent circuits of the transmission line are

Quick revision of Transformer Connection

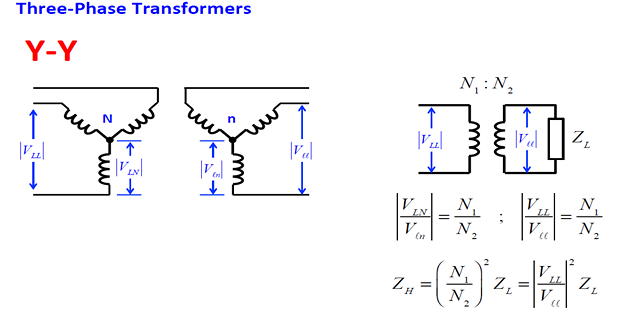
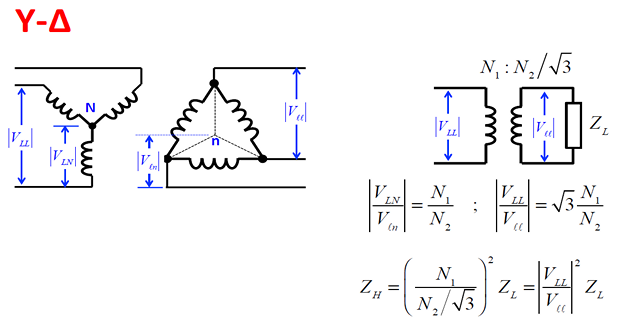
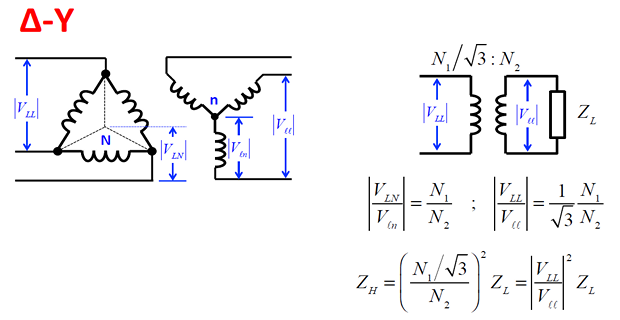
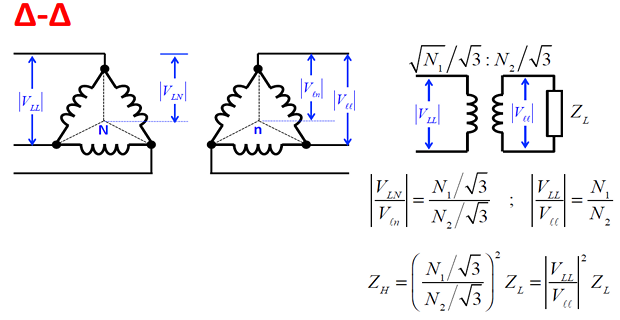
Sequence Circuits for Transformers

\[\begin{aligned} V_{A} & =V_{AN}+V_{N}\\ & =V_{AN}+3Z_{N}I_{A0}\\ V_{A0}+V_{A1}+V_{A2} & =V_{AN0}+V_{AN1}+V_{AN2}+3Z_{N}I_{A0} \end{aligned}\]

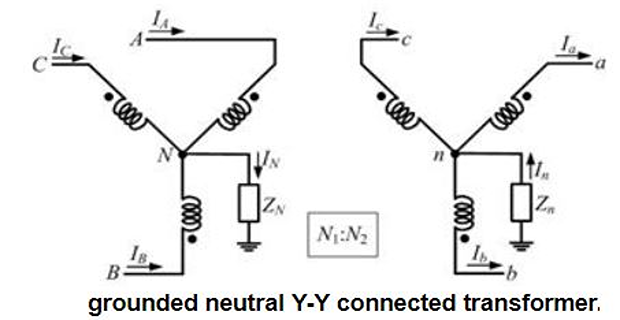
Direction of $I_n$ is opposite to that of $I_N$, we can write an similar equation for the secondary side as

\[\begin{aligned} V_{a0}+V_{a1}+V_{a2} & =V_{an0}+V_{an1}+V_{an2}-3Z_{n}I_{a0}\\ & =\dfrac{1}{\alpha}\left(V_{AN0}+V_{AN1}+V_{AN2}\right)-3Z_{n}\alpha I_{A0}\\ \alpha\left(V_{a0}+V_{a1}+V_{a2}\right) & =V_{AN0}+V_{AN1}+V_{AN2}-3Z_{n}\alpha^{2}I_{A0}\\ & =V_{A0}+V_{A1}+V_{A2}-3\left(Z_{N}+Z_{n}\alpha^{2}\right)I_{A0} \end{aligned}\]

\[\begin{aligned} \alpha & =\dfrac{N_{1}}{N_{2}} =\dfrac{V_{AN}}{V_{an}}\\ \Rightarrow V_{an}&=\dfrac{V_{AN}}{\alpha}\\ N_{1}I_{A} & =N_{2}I_{a}\Rightarrow I_{a}=\alpha I_{A} \end{aligned}\]

\[\begin{aligned} \alpha V_{a1} & =\dfrac{N_{1}}{N_{2}}V_{a1}=V_{A1}\\ \alpha V_{a2} & =\dfrac{N_{1}}{N_{2}}V_{a2}=V_{A2}\\ \alpha V_{a0} & =\dfrac{N_{1}}{N_{2}}V_{a0}=V_{A0}-3\left[Z_{N}+\left(N_{1}/N_{2}\right)^{2}Z_{n}\right]I_{A0} \end{aligned}\]
Separating out the positive, negative and zero sequence components
the positive and negative sequence impedances are the same as the transformer leakage impedance $Z$
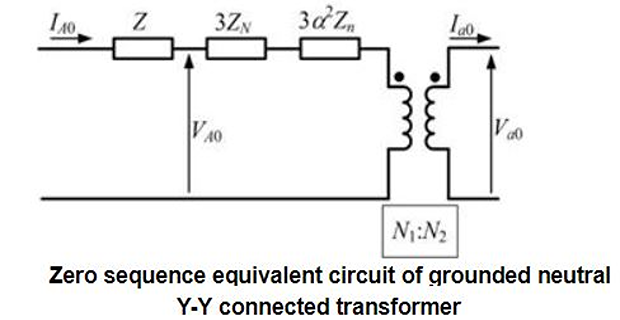
\[Z_{0}=Z+3Z_{N}+3\left(N_{1}/N_{2}\right)^{2}Z_{n}\]
The total zero sequence impedance is given by

If both the neutrals are solidly grounded, i.e., $Z_n = Z_ N = 0$, then $Z_0$ is equal to $Z$

\[\begin{aligned} V_{AB} & =V_{A}-V_{B}\\ & =\left(V_{A0}+V_{A1}+V_{A2}\right)-\left(V_{B0}+V_{B1}+V_{B2}\right)\\ & =V_{AB1}+V_{AB2} \end{aligned}\]

Therefore Again

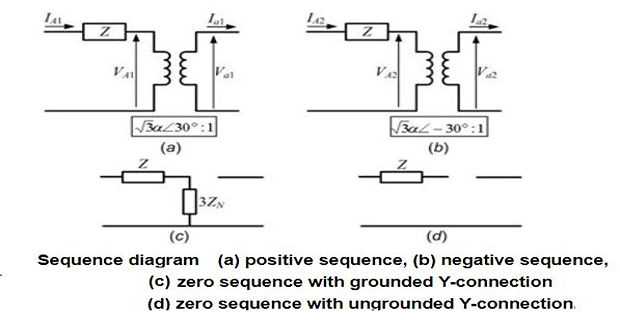
\[\begin{aligned} V_{AB1} & =\sqrt{3}V_{AN1}\angle30^{0}\\ V_{AB2} & =\sqrt{3}V_{AN2}\angle-30^{0} \end{aligned}\]
can be written in terms of the sequence components of the line-to-neutral voltage as The sequence components of the line-to-line voltage
\[\begin{aligned} \sqrt{3}V_{AN1}\angle30^{0}+\sqrt{3}V_{AN2}\angle-30^{0}&=\\ \alpha\left(\sqrt{3}V_{an1}\angle30^{0}+\sqrt{3}V_{an2}\angle-30^{0}\right)& \end{aligned}\]
Therefore combining we get
\[V_{AN1}=\alpha V_{an1}~\quad~V_{AN2}=\alpha V_{an2}\]
Hence we get

Thus the positive and negative sequence equivalent circuits are represented by a series impedance that is equal to the leakage impedance of the transformer.
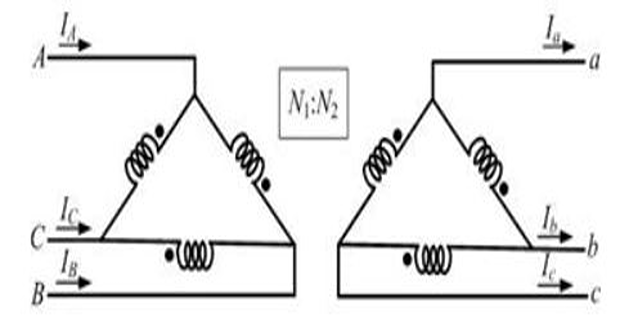
\[I_{A0}=I_{a0}=0\]
-connected winding does not provide any path for the zero sequence current to flow we have Since the
However the zero sequence current can sometimes circulate within the $\varDelta$ windings.

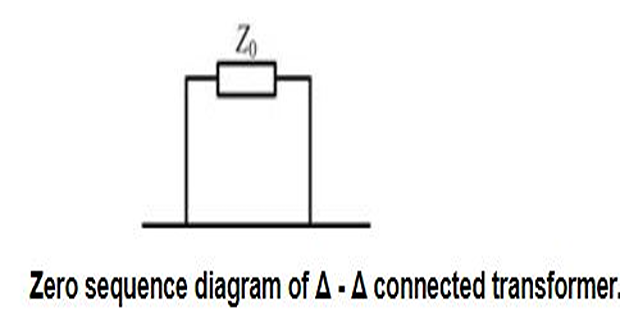
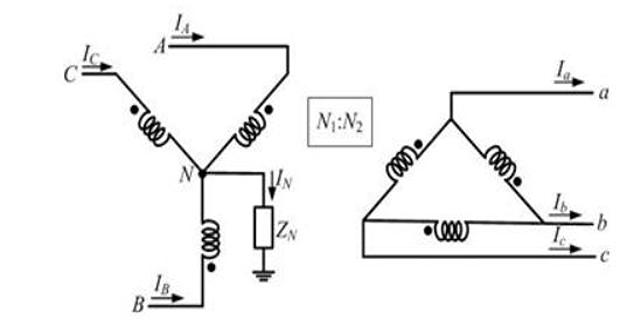
Even though $I_0$ in the primary Y-connected side has a path to the ground, the $I_0$ flowing in the $\varDelta$-connected secondary winding has no path to flow in the line.
Hence we have $I_{a0} = 0$.
However the circulating $I_0$ in the $\varDelta$ winding magnetically balances the $I_0$ of the primary winding.

\[V_{AN}=\dfrac{N_{1}}{N_{2}}V_{ab}=\alpha V_{ab}\]
The voltage in phase-a of both sides of the transformer
\[\begin{aligned} V_{A} & =V_{AN}+V_{N}\\ \left(V_{A0}+V_{A1}+V_{A2}\right) & =\left(V_{AN0}+V_{AN1}+V_{AN2}\right)+3Z_{N}I_{A0}\\ & =\alpha\left(V_{ab0}+V_{ab1}+V_{ab2}\right)+3Z_{N}I_{A0} \end{aligned}\]
Also
\[\begin{aligned} V_{A0} & =\alpha V_{ab0}+3Z_{N}I_{A0}\\ V_{A1} & =\alpha V_{ab1}=\sqrt{3}\alpha V_{a1}\angle30^{0}\\ V_{A2} & =\alpha V_{ab2}=\sqrt{3}\alpha V_{a2}\angle-30^{0} \end{aligned}\]
Separating zero, positive and negative sequence components

The zero sequence is $Z_0 = Z + 3Z_N$.
Note that the primary and the secondary sides are not connected and hence there is an open circuit between them.
However since the zero sequence current flows through primary windings, a return path is provided through the ground.
If however, the neutral in the primary side is not grounded, i.e., $Z_N = \infty$, then the zero sequence current cannot flow in the primary side as well.
The sequence diagram is then shown as $Z_0 = Z$.

Zero sequence networks for different T/F Configuration

Sequence Networks

positive, negative & zero sequence networks are formed separately by combining the sequence circuits of all the individual elements.
Assumptions made while forming sequence networks are:

Apart from syn. M/C, network is made of static elements.
$\mathrm{V_{drop}}$ caused by the current in a particular sequence depends only on the impedance of that part of the network.
Positive & negative sequence impedances are equal for all static circuit components, while zero sequence component need not be the same
Sub-transient positive & negative sequence impedances of a synchronous M/C are equal.
Voltage sources are connected to the positive sequence circuits of the rotating machines.
No $I_1$ or $I_2$ flows between neutral and ground.

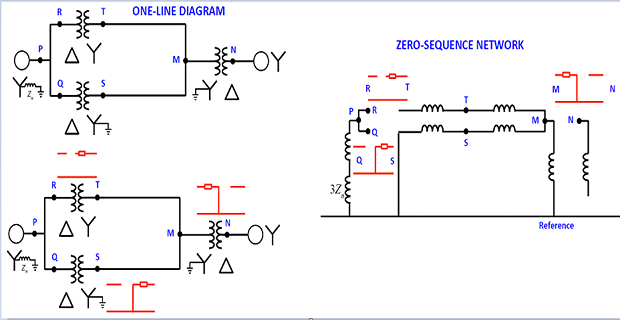
Sequence Network of a Power System