Demonstrative Video
Power-Angle Relationship
Consider the relation for a lumped parameter lossless transmission line
For a single-machine-infinite-bus (SMIB) system, the reactance \(X\) includes the reactance of the transmission line and the synchronous reactance or the transient reactance of the generator.
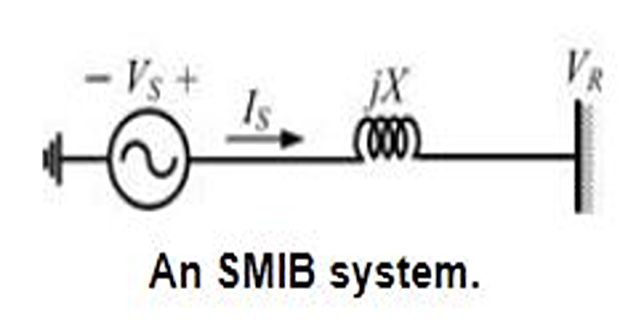
The sending end voltage is then the internal emf of the generator
Let the sending and receiving end voltage be given by
\[V_{s}=V_{1}\angle\delta,~~V_{r}=V_{2}\angle0^{0}\]
- \[I_{s}=\dfrac{V_{1}\angle\delta-V_{2}}{jX}=\dfrac{V_{1}cos\left(\delta\right)-V_{2}+jV_{1}sin\left(\delta\right)}{jX}\]We then have,
- \[\begin{aligned} P_{s}+jQ_{s} & =V_{s}I_{s}^{*}\\ &=V_{1}\left(cos~\delta+jsin~\delta\right)\dfrac{V_{1}cos~\delta-V_{2}-jV_{1}sin~\delta}{-jX}\\ & =\dfrac{V_{1}V_{2}sin~\delta+j\left(V_{1}^{2}-V_{1}V_{2}cos~\delta\right)}{X} \end{aligned}\]The sending end real power and reactive power:
Since the line is loss less, \(P_s = P_r\)
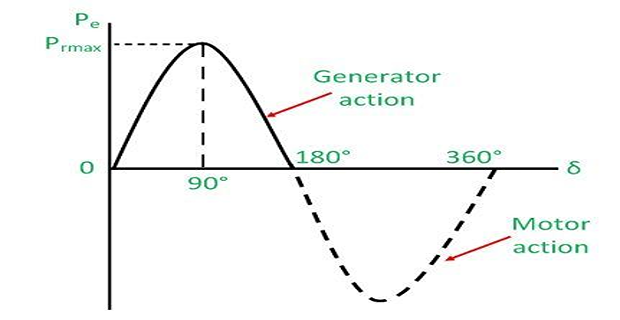
- \[\begin{aligned} P_{e}&=P_{s}=P_{r}\\ &=\dfrac{V_{1}V_{2}}{X}sin~\delta\\ &=P_{max}sin~\delta \end{aligned}\]We can therefore write
- \[P_{max} = V_1V_2/X\]where maximum power that can be transmitted over TL
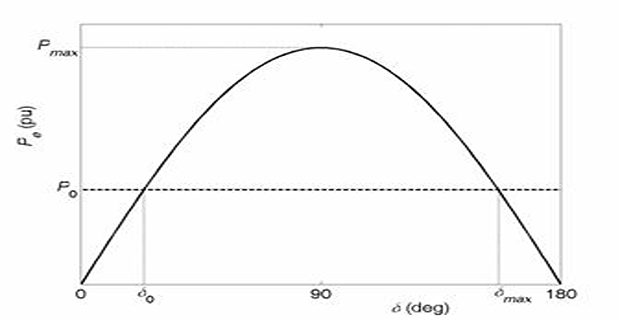
For a given power \(P_0\), there are two possible values of the angle \(\delta - \delta_0\) and \(\delta_{max}\).
- \[\begin{aligned} \delta_{0} & =sin^{-1}\left(\dfrac{P_{0}}{P_{max}}\right)\\ \delta_{max} & =180^{0}-\delta_{0} \end{aligned}\]The angles are given by