Demonstrative Video
Long transmission line
TL having a length more than 240 km
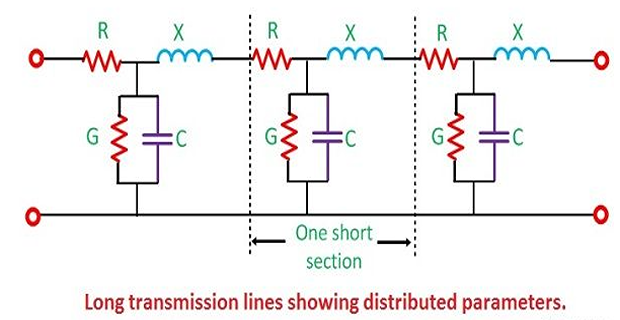
Parameters are uniformly distributed along the whole length of the line.
Line may be divided into various sections, and each section consists of an inductance, capacitance, resistance and conductance
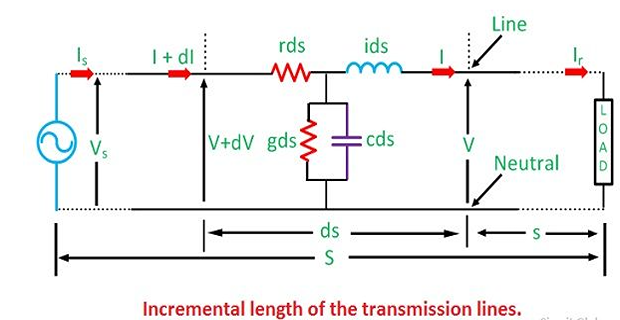
\[\begin{aligned}
dV_{x} & =I_{x}zdx\Rightarrow\dfrac{dV_{x}}{dx}=zI_{x}\\
dI_{x} & =V_{x}ydx\Rightarrow\dfrac{dI_{x}}{dx}=yV_{x}
\end{aligned}\]
\[\dfrac{d^{2}V_{x}}{dx^{2}}=\dfrac{dI_{x}}{dx}z=yV_{x}z\]
\[\dfrac{dV_{x}}{dx}=C_{1}\gamma e^{\gamma
x}-C_{2}\gamma e^{-\gamma x}=zI_{x}\]
\[\boxed{Z_{c}=\sqrt{\left(\dfrac{z}{y}\right)}}\]
\[\therefore I_{x}=\dfrac{C_{1}}{Z_{c}}e^{\gamma
x}-\dfrac{C_{2}}{Z_{c}}e^{-\gamma x}\]
where
\[\begin{aligned}
V_{x}&=C_{1}e^{\gamma x}+C_{2}e^{-\gamma x}\\
I_{x}&=\dfrac{C_{1}}{Z_{c}}e^{\gamma
x}-\dfrac{C_{2}}{Z_{c}}e^{-\gamma x}
\end{aligned}\]
Applying boundary condition:
\[\begin{aligned}
V_{x} & =V_{R}\left(\dfrac{e^{\gamma x}+e^{-\gamma
x}}{2}\right)+I_{R}Z_{c}\left(\dfrac{e^{\gamma x}-e^{-\gamma
x}}{2}\right)\\
&=V_{R}cosh\left(\gamma x\right)+I_{R}Z_{c}sinh\left(\gamma
x\right)
\end{aligned}\]
\[\begin{aligned}
I_{x} & =V_{R}\dfrac{1}{Z_{c}}\left(\dfrac{e^{\gamma
x}-e^{-\gamma x}}{2}\right)e^{\gamma x}+I_{R}\left(\dfrac{e^{\gamma
x}+e^{-\gamma x}}{2}\right)\\
&=I_{R}cosh\left(\gamma
x\right)+V_{R}\dfrac{1}{Z_{c}}sinh\left(\gamma x\right)
\end{aligned}\]
when
$$\boxed{
\left[\begin{array}{c}
V_S \\
I_S
\end{array}\right]=\left[\begin{array}{cc}
\cosh (\gamma l) & Z_c \sinh (\gamma l) \\
\frac{1}{Z_c} \sinh (\gamma l) & \cosh (\gamma l)
\end{array}\right]\left[\begin{array}{c}
V_R \\
I_R
\end{array}\right]
}$$
Evaluation of ABCD constants of Long TL
\[\gamma=\sqrt{yz}=\alpha+j\beta\]
The hyperbolic function of complex numbers involved in evaluating ABCD
constants can be computed by any of the following three methods:
\[\begin{aligned}
cosh\left(\alpha l+j\beta l\right) & =cosh\left(\alpha
l\right)cos\left(\beta l\right)+jsinh\left(\alpha l\right)sin\left(\beta
l\right)\\
sinh\left(\alpha l+j\beta l\right) & =sinh\left(\alpha
l\right)cos\left(\beta l\right)+jcosh\left(\alpha l\right)sin\left(\beta
l\right)
\end{aligned}\]
The trigonometric values can be looked from standard tables.
\[\begin{aligned}
cosh\left(\gamma l\right) &
=1+\dfrac{\gamma^{2}l^{2}}{2!}+\dfrac{\gamma^{4}l^{4}}{4!}+\cdots\approx\left(1+\dfrac{YZ}{2}\right)\\
sinh\left(\gamma l\right) & =\gamma
l+\dfrac{\gamma^{3}l^{3}}{3!}+\dfrac{\gamma^{5}l^{5}}{5!}+\cdots\approx\sqrt{YZ}\left(1+\dfrac{YZ}{6}\right)
\end{aligned}\]
and can be conveniently
approximated This series converges rapidly for values of
\[\begin{aligned}
cosh\left(\alpha l+j\beta l\right) & =\dfrac{1}{2}\left(e^{\alpha
l}\angle\beta l+e^{-\alpha l}\angle-\beta l\right)\\
sinh\left(\alpha l+j\beta l\right) & =\dfrac{1}{2}\left(e^{\alpha
l}\angle\beta l-e^{-\alpha l}\angle-\beta l\right)
\end{aligned}\]
Interpretation of the long line equations
\[\gamma=\alpha+j\beta\]
| Real part \(\alpha\) : | |
| Imaginary part \(\beta\) : |
\[\begin{aligned}
V_{x} & =\left|\dfrac{V_{R}+I_{R}Z_{c}}{2}\right|e^{\alpha
x}e^{j\left(\beta
x+\phi_{1}\right)}+\left|\dfrac{V_{R}-I_{R}Z_{c}}{2}\right|e^{-\alpha
x}e^{-j\left(\beta x-\phi_{2}\right)}
\end{aligned}\]
Instantaneous voltage, \(v_{x}\left(t\right) =v_{x1}+v_{x2}\)
\[\begin{cases}
v_{x1} &
=\sqrt{2}\left|\dfrac{V_{R}+I_{R}Z_{c}}{2}\right|e^{\alpha
x}cos\left(\omega t+\beta x+\phi_{1}\right)\\
v_{x2} &
=\sqrt{2}\left|\dfrac{V_{R}-I_{R}Z_{c}}{2}\right|e^{-\alpha
x}cos\left(\omega t-\beta x+\phi_{2}\right)
\end{cases}\]
\[\begin{aligned}
\phi_{1} & = \angle\left(V_{R}+I_{R}Z_{c}\right)\\
\phi_{2} & = \angle\left(V_{R}-I_{R}Z_{c}\right)
\end{aligned}\]
where:
\(v_{x}\left(t\right)\) is a function of two variables - time & distance
Represents two travelling waves: Incident and reflected waves
