Line-to-Line (LL) Faults in Power Systems
Demonstrative Video
Line-to-Line Fault
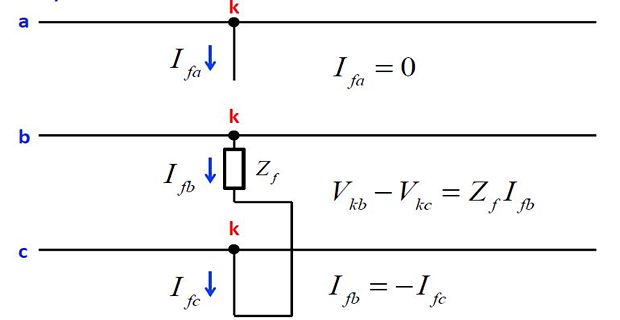
Line-to-Line fault is being regarded in phase \(b\) and \(c\)
Substituting:
\[\begin{aligned} \left[\begin{array}{c} I_{fa}^{(0)}\\ I_{fa}^{(1)}\\ I_{fa}^{(2)} \end{array}\right]& = \dfrac{1}{3}\left[\begin{array}{ccc} 1 & 1 & 1\\ 1 & a & a^{2}\\ 1 & a^{2} & a \end{array}\right]\left[\begin{array}{c} 0\\ I_{fb}\\ -I_{fc} \end{array}\right]\\ &\Rightarrow I_{fa}^{(0)} =0\\ &\Rightarrow I_{fa}^{(1)} =-I_{fa}^{(2)} \end{aligned}\]
The voltages throughout the zero-sequence network must be zero since there are no zero-sequence sources, and because \(I_{fa}^{(0)} = 0\), current is not being injected into that network due to the fault.
Hence, line-to‐line fault calculation do not involve the zero-sequence network, which remains the same as before the fault - a dead network.
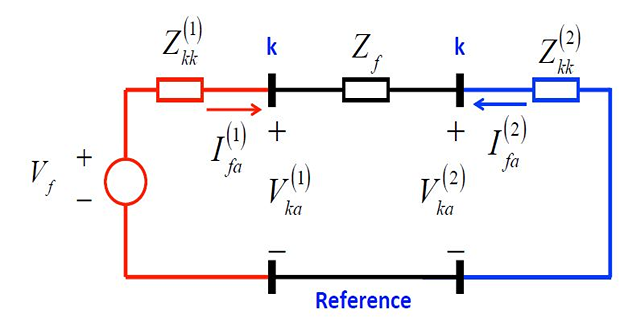
To satisfy the requirement \(I_{fa}^{(1)} = -I_{fa}^{(2)}\), we connect the Thevenin’s equivalents of positive and negative sequence networks in parallel
To show that this connection of the networks also satisfies the voltage equation: \[V_{kb} - V_{kc} = Z_fI_{fb}\]
we now expand each side of that equation separately as follows:
\[\begin{aligned} V_{kb}-V_{kc} & =\left(V_{kb}^{(1)}+V_{kb}^{(2)}\right)-\left(V_{kc}^{(1)}+V_{kc}^{(2)}\right)\\ & =\left(V_{kb}^{(1)}-V_{kc}^{(1)}\right)+\left(V_{kb}^{(2)}-V_{kc}^{(2)}\right)\\ & =\left(\alpha^{2}-\alpha\right)V_{ka}^{(1)}+\left(\alpha-\alpha^{2}\right)V_{ka}^{(2)}\\ & =\left(\alpha^{2}-\alpha\right)\left(V_{ka}^{(1)}-V_{ka}^{(2)}\right) \end{aligned}\]
and \[\begin{aligned} Z_{f}I_{fb}&=Z_{f}\left(I_{fb}^{(1)}+I_{fb}^{(2)}\right)\\ &=Z_{f}\left(\alpha^{2}I_{fa}^{(1)}+\alpha I_{fa}^{(2)}\right) \end{aligned}\]
equate both terms and set \(I_{fa}^{(1)} = -I_{fa}^{(2)}\) \[\begin{aligned} V_{kb}-V_{kc} & =\left(\alpha^{2}-\alpha\right)\left(V_{ka}^{(1)}-V_{ka}^{(2)}\right)\\ &=Z_{f}I_{fb}\\ &=Z_{f}\left(\alpha^{2}I_{fa}^{(1)}+\alpha I_{fa}^{(2)}\right)\\ \Rightarrow\left(\alpha^{2}-\alpha\right)\left(V_{ka}^{(1)}-V_{ka}^{(2)}\right) & =Z_{f}\left(\alpha^{2}-\alpha\right)I_{fa}^{(1)}\\ \Rightarrow V_{ka}^{(1)}-V_{ka}^{(2)} & =Z_{f}I_{fa}^{(1)} \end{aligned}\]
Thus, all the fault conditions are satisfied by connecting the positive and negative sequence networks in parallel through impedance \(Z_f\) .
The zero-sequence network is inactive and does not enter into the line-to-line calculation.