Ferranti Effect in Transmission Lines

Demonstrative Video

Ferranti effect

  • The effect of the TL in which \(V_r > V_s\) is known as the Ferranti effect.

  • Mainly occurs because of light load or open circuit at the receiving end

  • Ferranti effect is due to the charging current of the line.

  • When an ac voltage is applied, the current that flows into the capacitor is called charging current.

  • A charging current is also known as capacitive current.

  • The charging current increases in the line when \(V_r~>~V_s\)

  • The effect of the line capacitance is to cause the no-load receiving end voltage to be more than the sending end voltage

  • Effect is more pronounced as the line length increases

Cause of Ferranti Effect

  • \(C\) and \(L\) are the main parameters of the lines having a length 240 km or above.

  • On such TL, \(C\) is not concentrated at some definite points. It is distributed uniformly along the whole length of the line.

  • For \(V_s\) the current drawn by the capacitance of the line is more than current associated with the load.

  • Thus, at no load or light load, the \(V_r\) is quite large as compared to the constant voltage at the sending end.

  • \[V_{S}=\dfrac{V_{R}}{2}e^{\alpha l}e^{j\beta l}+\dfrac{V_{R}}{2}e^{-\alpha l}e^{-j\beta l}\]
    (no load) and Substituting

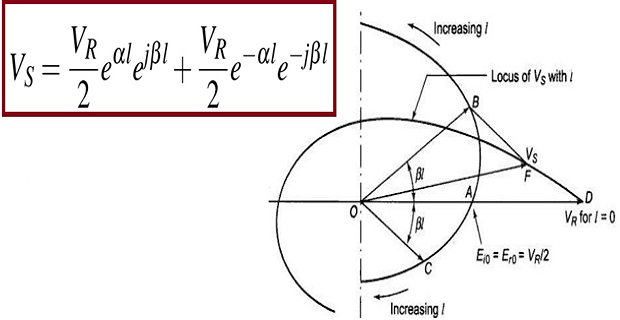
image

  • At \(l = 0\), both incident and reflected waves is \(V_{R}/2\)

  • As \(l\) increases

    • incident wave increases exponentially with \(\dfrac{V_{R}}{2} e^{\alpha t}\) and turns through positive angle \(\beta l\) (\(OB\))

    • reflected wave decreases exponentially with \(\dfrac{V_{R}}{2} e^{-\alpha t}\) and turns through negative angle \(\beta l\) (\(OC\))

  • The resultant phasor \(V_S\) (OF) is such that \(\left|V_{R}\right|>\left|V_{S}\right|\)

Ferranti effect explained by phasor diagram:

\[\begin{aligned} V_{r} & =V_{r}(1+j 0)\\ I_{c} & =j \omega C V_{r}\\ V_{s} & =V_{r}+\text {resistive drop}+\text {reactive drop}\\ &=V_{r}+I_{c} R+j I_{c} X\\ &=V_{r}+I_{c}(R+j X)\\ &=V_{r}+j \omega C V_{r}(R+j \omega L)~~[\text { since } X=\omega L]\\ V_{s} & =V_{r}-\omega^{2} C L V_{r}+j \omega C R V_{r} \end{aligned}\]
\[\begin{aligned} V_{s}^{2}&=\left(V_{r}-I_{c} X_{L}\right)^{2}+\left(I_{c} R\right)^{2} \\ V_{s}&=V_{r}-\omega^{2} L C V_{r} ~~[R~\text{ is negligeble in long TL}]\\ V_{s}&=V_{r}-I_{c} X_{L} \\ V_{r}&=V_{s}+I_{c} X_{L} \end{aligned}\]
\[\begin{array}{c} V_{s}=\left(1+\dfrac{Y Z}{2}\right) V_{r} \\ V_{s}-V_{r}=\dfrac{Y Z}{2} V_{r} \end{array}\]
\(I_r=0\)\(\Pi\)From Phasor diagram
\[\begin{aligned} V_{s}-V_{r} &=\dfrac{(j \omega C l)(r+j \omega L) l}{2} V_{r} \\ V_{s}-V_{r} &=\dfrac{-\omega^{2} C l^{2}}{2} L V_{r} ~~ [\text{Subs.}~ r=0]\\ V_{s} &=\left(1-\dfrac{\omega^{2} C l^{2}}{2} L\right) V_{r} \end{aligned}\]
Substituting the expression of impedance and admittance