Equal Area Criterion for Power System Stability

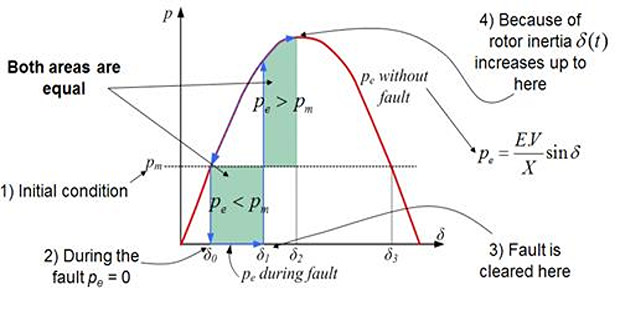
Consider the situation in which the synchronous machine is operating in steady state delivering a power \(P_e = P_m\) when there is a fault occurs in the system.
Opening up of the circuit breakers in the faulted section subsequently clears the fault.
The circuit breakers take about 5/6 cycles to open and the subsequent post-fault transient last for another few cycles.
The input power, on the other hand, is supplied by a prime mover that is usually driven by a steam turbine.
The time constant of the turbine mass system is of the order of few seconds, while the electrical system time constant is in milliseconds.
Therefore, for all practical purpose, \(P_m\) remains constant during this period when the electrical transients occur.

The transient stability study therefore concentrates on the ability of the power system to recover from the fault and deliver the constant power \(P_m\) with a possible new load angle \(\delta\).
Suppose the system is operating in the steady state delivering \(P_m\) at an angle of \(\delta_0\) when due to malfunction of the line, circuit breakers open reducing the real power transferred to zero.
Since \(P_m\) remains constant, \(P_a\) becomes equal to \(P_m\).
The difference in the power gives rise to the rate of change of stored kinetic energy in the rotor masses.
Thus the rotor will accelerate under the constant influence of non-zero accelerating power and hence \(\delta\) will increase.

Now suppose the circuit breaker re-closes at an angle \(\delta_c\).
The power will then revert back to the normal operating curve.
At that point, \(P_e > P_m \Rightarrow P_a = -ve\)
Machine will decelerate, and due to the inertia of the rotor masses, \(\delta\) will still keep on increasing.
The increase in this angle may eventually stop and the rotor may start decelerating, otherwise the system will lose synchronism.
\[\dfrac{d}{dt}\left(\dfrac{d\delta}{dt}\right)^{2}=2\left(\dfrac{d\delta}{dt}\right)\left(\dfrac{d^{2}\delta}{dt^{2}}\right)\]
Since,
\[\dfrac{H}{\omega_{s}}\dfrac{d}{dt}\left(\dfrac{d\delta}{dt}\right)^{2}=\left(P_{m}-P_{e}\right)\dfrac{d\delta}{dt}\]
, we get Therefore, from

\[\left.\dfrac{H}{\omega_{s}}\left(\dfrac{d\delta}{dt}\right)^{2}\right|_{\delta_{0}}^{\delta_{c}}=\intop_{\delta_{0}}^{\delta_{c}}\left(P_{m}-P_{e}\right)d\delta\]
we get and Multiplying both sides of the above equation by dt and then integrating between two arbitrary angles
Now suppose the generator is at rest at \(\delta_0\). We then have \(d\delta/dt = 0\).
Once a fault occurs, the machine starts accelerating.
Once the fault is cleared, the machine keeps on accelerating before it reaches its peak at \(\delta_c\), at which point we again have \(d\delta/dt = 0\).

\[A_{1}=\intop_{\delta_{0}}^{\delta_{c}}\left(P_{m}-P_{e}\right)d\delta=0\]
Thus the area of accelerating is given as
\[A_{2}=\intop_{\delta_{0}}^{\delta_{c}}\left(P_{e}-P_{m}\right)d\delta=0\]
is given by Similarly, the area of deceleration,
Now consider the case when the line is re closed at \(\delta_c\) such that the area of \(A_{1} > A_2\) .
The generator load angle will then cross the point \(\delta_m\), beyond which the \(P_e < P_m \Rightarrow P_a = +ve\)

The generator will therefore start accelerating before is slows down completely and will eventually become unstable.
If \(A_{1} < A_2\), the machine will decelerate completely before accelerating again.
The rotor inertia will force the subsequent acceleration and deceleration areas to be smaller than the first ones and the machine will eventually attain the steady state.
If \(A_{1} = A_2\), defines the boundary of the
The clearing angle \(\delta_{c}\) for this mode is called the , \(\delta_{cr}\).

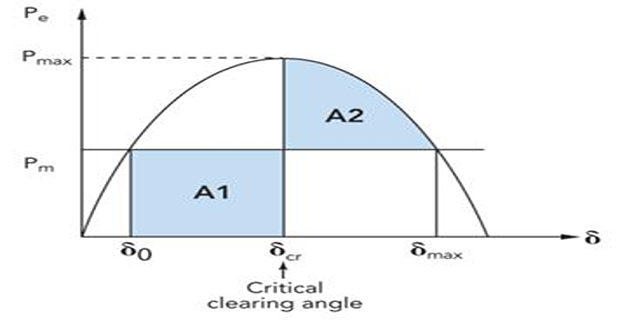
\[\intop_{\delta_{0}}^{\delta_{cr}}\left(P_{m}-P_{e}\right)d\delta=\intop_{\delta_{cr}}^{\delta_{m}}\left(P_{e}-P_{m}\right)d\delta\]
We then get by substituting
We can calculate the critical clearing angle from the above equation.
Since the critical clearing angle depends on the equality of the areas, this is called the .

Since we are interested in finding out the maximum time that the circuit breakers may take for opening, we should be more concerned about the rather than clearing angle.
Furthermore, notice that the clearing angle is independent of the generalized inertia constant H.
The critical clearing time, however, is dependent on \(H\) and will vary as this parameter varies.
To obtain a description for the critical clearing time, let us consider the period during which the fault occurs.
We then have \(P_e = 0\).

\[\dfrac{d^{2}\delta}{dt^{2}}=\dfrac{\omega_{s}}{2H}P_{m}\]
We can therefore write from
\[\dfrac{d\delta}{dt}=\intop_{0}^{t}\left(\dfrac{\omega_{s}}{2H}P_{m}\right)dt=\dfrac{\omega_{s}}{2H}P_{m}t\]
Integrating with the initial acceleration being zero we get
\[\delta=\intop_{0}^{t}\left(\dfrac{\omega_{s}}{2H}P_{m}t\right)dt=\dfrac{\omega_{s}}{4H}P_{m}t^{2}+\delta_{0}\]
Further integration will lead to
\[t_{cr}=\sqrt{\dfrac{4H}{\omega_{s}P_{m}}\left(\delta_{cr}-\delta_{0}\right)}\]
, we get the critical clearing time as and Replacing