Effect of Earth on Transmission Line Capacitance

Demonstrative Video

Effect of earth on the capacitance of a three-phase line

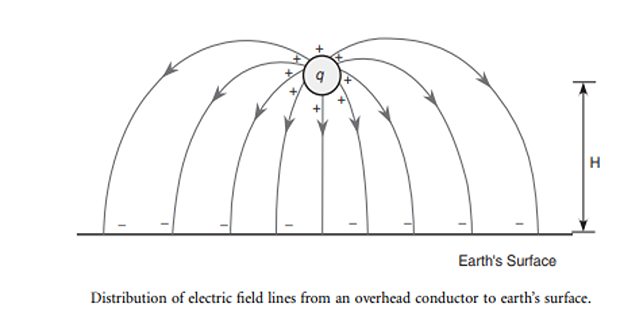
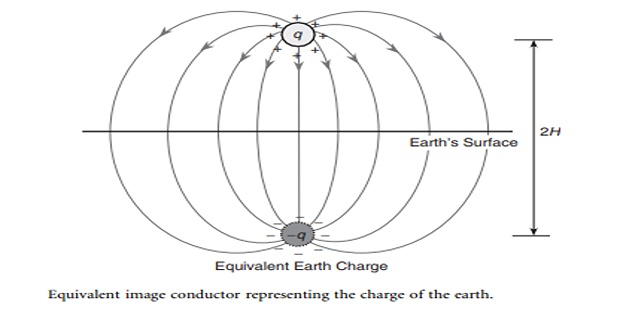
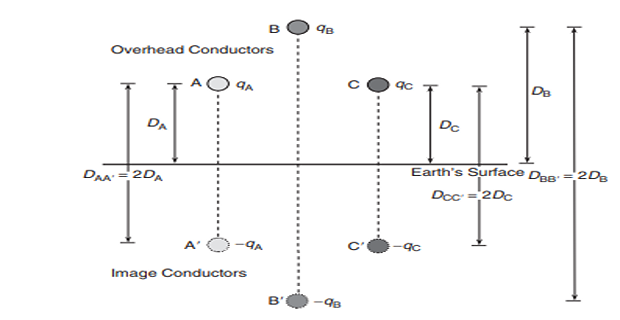
image
image
image

  • Earth alters the electric field of the line, hence the capacitance is affected

  • Assume earth to be a perfect conductor- horizontal plane of infinite extent

  • Electric field of the charged conductor above the earth not the same if equipotential surface of the earth were not present

  • Consider a single conductor with an earth return

  • Charge comes from earth to reside on the conductor and a potential difference exists between the conductor and earth

  • The earth and conductor have charge equal in magnitude but of opposite sign

  • The electric flux from the charges on the conductor to the charges on the earth is perpendicular to the earth’s equipotential surface since surface is assumed to be a perfect conductor

\[\begin{aligned} \mathrm{v_{ab}}&=\frac{1}{2 \pi \varepsilon}\left[q_{a} \ln \frac{D}{r}+q_{b} \ln \frac{r}{D}\right]+\frac{1}{2 \pi \varepsilon}\left[-q_{a} \ln \frac{H}{2 h}-q_{b} \ln \frac{2 h}{H}\right] \\ \text {but} \quad H& =\sqrt{D^{2}+(2 h)^{2}}=\sqrt{D^{2}+4 h^{2}} \end{aligned}\]
\[\begin{aligned} \therefore v_{a b}& =\frac{1}{2 \pi \varepsilon}\left[q_{a} \ln \frac{D}{r}+q_{b} \ln \frac{r}{D}\right]+ \\ &\frac{1}{2 \pi \varepsilon}\left[-q_{a} \ln \frac{\sqrt{D^{2}+4 h^{2}}}{2 h}-q_{b} \ln \frac{2 h}{\sqrt{D^{2}+4 h^{2}}}\right] \end{aligned}\]
\[\begin{aligned} \mathrm{v_{ab}}&=\frac{1}{2 \pi \varepsilon}\left[q_{a} \ln \frac{2 h D}{r \sqrt{D^{2}+4 h^{2}}}+q_{b} \ln \frac{r \sqrt{D^{2}+4 h^{2}}}{2 h D}\right] \end{aligned}\]
\[\text { but } \quad q_{a}=-q_{b}\]
\[\begin{aligned} \therefore \mathrm{v_{ab}}&=\frac{1}{2 \pi \varepsilon}\left[q_{a} \ln \frac{4 h^{2} D^{2}}{r^{2}\left(D^{2}+4 h^{2}\right)}\right] \\ &=\frac{1}{2 \pi \varepsilon}\left[q_{a} \ln \left(\frac{D}{r \sqrt{1+\left(D^{2} / 4 h^{2}\right)}}\right)^{2}\right]\\ &=\frac{1}{2 \pi \varepsilon}\left[2 q_{a} \ln \frac{D}{r \sqrt{1+\left(D^{2} / 4 h^{2}\right)}}\right] \\ &= \frac{q_{a}}{\pi \varepsilon}\left[\ln \frac{D}{r}+\ln \frac{1}{\sqrt{1+\left(D^{2} / 4 h^{2}\right)}}\right] \quad \text { volts } \end{aligned}\]

  • Imagine a fictitious conductor (same size and shape) lying directly below the original conductor at the same distance

  • Earth is removed and equal and opposite charge is assumed on the fictitious conductor

    1. plane midway acts as equipotential plane

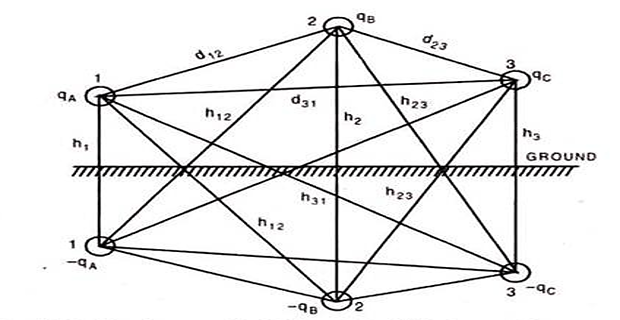
image

  • Applying the method of images and assuming the line is transposed carrying the charges \(q_{a}, q_{b}\) and \(q_c\) and occuping position 1, 2, and 3, respectively, in the first part of the transposition cycle.

  • \[ V_{ab}=\dfrac{1}{2\pi\varepsilon}\left[q_{a}\left(ln\dfrac{D_{12}}{r}-ln\dfrac{H_{12}}{H_{1}}\right)+q_{b}\left(ln\dfrac{r}{D_{12}}-ln\dfrac{H_{2}}{H_{12}}\right)+q_{c}\left(ln\dfrac{D_{23}}{D_{31}}-ln\dfrac{H_{23}}{H_{31}}\right)\right] \]
    in position 3 in position 2, and in position 1, With

  • Knowing the sum of charges is zero, finally

    equation* C_n= F/m

  • Effect of earth is to increase the capacitance of the line

  • If conductors are very high above ground, \(H_1\) and \(H_{12}\), and others are nearly equal
    \(\checkmark\) effect of ground is neglected, except when sum of three line currents is not zero.