Demonstrative Video
Double-Line-to-Ground Fault
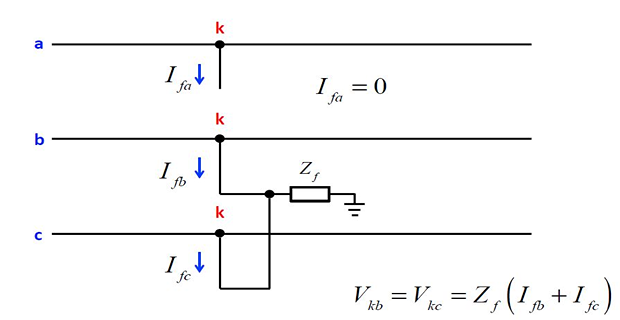
Since,
\[\begin{aligned} I_{fa} & =0\Rightarrow I_{fa}^{(0)}=\dfrac{1}{3}\left(I_{fa}+I_{fb}+I_{fc}\right)=\dfrac{1}{3}\left(I_{fb}+I_{fc}\right)\\ \Rightarrow V_{kb} & =V_{kc}=Z_{f}\left(I_{fb}+I_{fc}\right)=3Z_{f}I_{fa}^{(0)} \end{aligned}\]Substituting into:
\[\begin{aligned} \left[\begin{array}{c} V_{ka}^{(0)}\\ V_{ka}^{(1)}\\ V_{ka}^{(2)} \end{array}\right] & =\dfrac{1}{3}\left[\begin{array}{ccc} 1 & 1 & 1\\ 1 & a & a^{2}\\ 1 & a^{2} & a \end{array}\right]\left[\begin{array}{c} V_{ka}\\ V_{kb}\\ V_{kc} \end{array}\right]\\ & =\dfrac{1}{3}\left[\begin{array}{ccc} 1 & 1 & 1\\ 1 & a & a^{2}\\ 1 & a^{2} & a \end{array}\right]\left[\begin{array}{c} V_{ka}\\ V_{kb}\\ V_{kb} \end{array}\right] \end{aligned}\]
- \[\begin{aligned} V_{ka}^{(1)} & =\dfrac{1}{3}\left(\alpha+\alpha^{2}\right)V_{kb}\\ V_{ka}^{(2)} & =\dfrac{1}{3}\left(\alpha^{2}+\alpha\right)V_{kb}\\ \Rightarrow V_{ka}^{(1)} & =V_{ka}^{(2)} \end{aligned}\]Expanding the second and third equations:
- \[3V_{ka}^{(0)}=V_{ka}+2V_{kb}=\left(V_{ka}^{(0)}+V_{ka}^{(1)}+V_{ka}^{(2)}\right)+2\left(3Z_{f}I_{fa}^{(0)}\right)\]From the first equation:
- \[\begin{aligned} V_{kb} & =V_{kc}=Z_{f}\left(I_{fb}+I_{fc}\right)\\ 3I_{fa}^{(0)} & =I_{fb}+I_{fc} \end{aligned}\]Recall;
- \[3V_{ka}^{(0)} = V_{ka}^{(0)} + 6Z_fI_{fa}^{(0)} + 2V_{ka}^{(1)}\]Collect zero-sequence terms and recall that
- \[V_{ka}^{(1)}= V_{ka}^{(0)} - 3Z_fI_{fa}^{(0)}\]Now solve:
- \[V_{ka}^{(1)} = V_{ka}^{(2)} = V_{ka}^{(0)} - 3Z_fI_{fa}^{(0)}\]Thus,
- \[I_{fa}^{(0)}+I_{fa}^{(1)}+I_{fa}^{2} =0\]and since
These last two results characterize the double line-to-ground fault
realized by putting all three sequence networks in parallel as follows:
\[I_{fa}^{(1)}=\dfrac{V_{f}}{Z_{kk}^{(1)}+\left(Z_{kk}^{(0)}+3Z_{f}\right)||
Z_{kk}^{(2)}}=\dfrac{V_{f}}{Z_{kk}^{(1)}+\dfrac{\left(Z_{kk}^{(0)}+3Z_{f}\right)Z_{kk}^{(2)}}{Z_{kk}^{(0)}+Z_{kk}^{(2)}+3Z_{f}}}\]
\[I_{fa}^{(2)}=-I_{fa}^{(1)}\dfrac{Z_{kk}^{(0)}+3Z_{f}}{Z_{kk}^{(0)}+Z_{kk}^{(2)}+3Z_{f}},~~I_{fa}^{(0)}=-I_{fa}^{(1)}\dfrac{Z_{kk}^{(2)}}{Z_{kk}^{(0)}+Z_{kk}^{(2)}+3Z_{f}}\]
Clearly:
For a bolted fault \(Z_f\) is set equal to 0.
When \(Z_f = \infty\), the zero-sequence circuit becomes an open circuit, no zero-sequence current an flow, and the equations revert back to those for the line-to-line fault
Once sequence currents are calculated at the fault bus \(k\), Sequence voltage changes at all buses of the system can then be calculated from \(Z_{bus}\)