Capacitance of Bundled Conductors

Conductors of any one bundle are in parallel and the charge per bundle divides equally between the conductors of the bundle
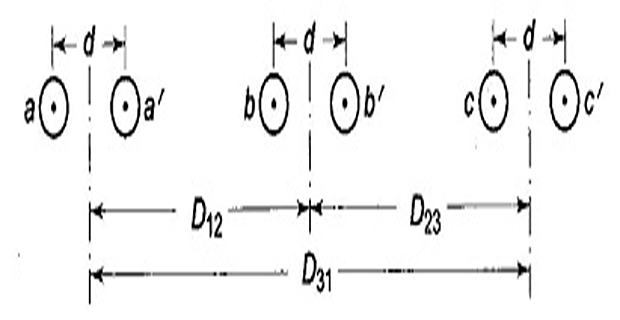
separation between bundles is usually more than 15 times the spacing between the conductors of the bundle
\(D_{12} \ggg d\), Use \(D_{12}\) for \(\left(D_{12} ~ \pm ~ d\right)\)

If charge on phase \(a\) is \(q_a\), conductors \(a\) and \(a^{'}\) has the charge \(q_{a}/2\), and similarly for \(b\) and \(c\)

\[ V_{ab}=\dfrac{1}{2\pi\varepsilon}\left[\dfrac{q_{a}}{2}\left(\begin{array}{c} \underbrace{ln\dfrac{D_{12}}{r}}\\ a \end{array}+\begin{array}{c} \underbrace{ln\dfrac{D_{12}}{d}}\\ a^{'} \end{array}\right)+\dfrac{q_{b}}{2}\left(\begin{array}{c} \underbrace{ln\dfrac{r}{D_{12}}}\\ b \end{array}+\begin{array}{c} \underbrace{ln\dfrac{d}{D_{12}}}\\ b^{'} \end{array}\right)+\dfrac{q_{c}}{2}\left(\begin{array}{c} \underbrace{ln\dfrac{D_{23}}{D_{31}}}\\ c \end{array}+\begin{array}{c} \underbrace{ln\dfrac{D_{23}}{D_{31}}}\\ c^{'} \end{array}\right)\right] \]
\[V_{ab}=\dfrac{1}{2\pi\varepsilon}\left(q_{a}~ln\dfrac{D_{12}}{\sqrt{r\cdot d}}+q_{b}~ln\dfrac{\sqrt{r\cdot d}}{D_{12}}+q_{c}~ln\dfrac{D_{23}}{D_{31}}\right)\]
Combining the terms, we get
\[\boxed{C_{n}=\dfrac{2\pi\varepsilon}{ln\left(\dfrac{D_{eq}}{\sqrt{r\cdot d}}\right)}~F/m}\]

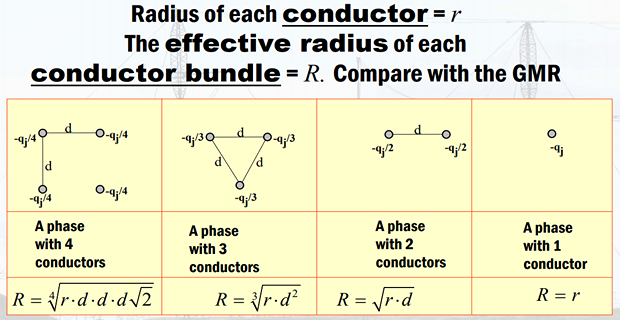
For different strands

\[C_{n}=\dfrac{2\pi\varepsilon}{ln\left(\dfrac{D_{eq}}{D_{s}^{b}}\right)}~F/m\]

\[D_{s}^{b}=\begin{cases} \sqrt[4]{\left(r\times d\right)^{2}}=\sqrt{r\cdot d} & 2~\mbox{strand}\\ \sqrt[9]{\left(r\times d\times d\right)^{3}}=\sqrt[3]{r\cdot d} & 3~\mbox{strand}\\ \sqrt[16]{\left(r\times d\times d\times d\times\sqrt{2}\right)^{4}}=1.09\sqrt[4]{r\cdot d} & 4~\mbox{strand} \end{cases}\]