Capacitance of Three-Phase Transmission Lines

Demonstrative Video

Capacitance of a three-phase line

Overview of the topic:

  • equilateral spacing

  • unsymmetrical spacing & Transposition

  • Effect of earth on capacitance

\[\begin{aligned} V_{ab}&=\dfrac{1}{2\pi\varepsilon}\left(q_{a}~ln\dfrac{D}{r}+q_{b}~ln\dfrac{r}{D}+\underset{zero}{\underbrace{q_{c}~ln\dfrac{D}{D}}}\right)~V \\ V_{ac}&=\dfrac{1}{2\pi\varepsilon}\left(q_{a}~ln\dfrac{D}{r}+\underset{zero}{\underbrace{q_{b}~ln\dfrac{D}{D}}}+q_{c}~ln\dfrac{r}{D}\right)~V \end{aligned}\]
\[V_{ab}+V_{ac}=\dfrac{1}{2\pi\varepsilon}\left[2q_{a}~ln\dfrac{D}{r}+\left(q_{b}+q_{c}\right)~ln\dfrac{r}{D}\right]~V\]
\[V_{ab}+V_{ac}=\dfrac{3q_{a}}{2\pi\varepsilon}ln\dfrac{D}{r}~V\]
Since,
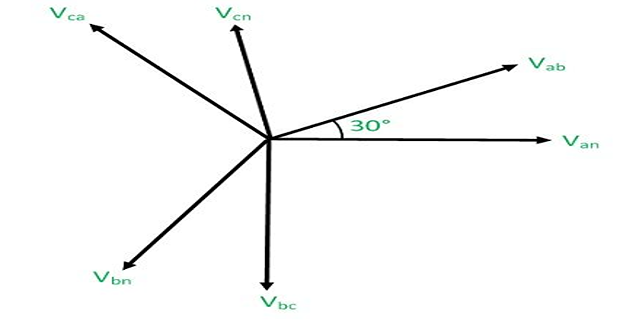
image
Phasor diagram of the balanced voltages of a \(3\phi\) line

  • Adding, \(V_{ab}+V_{ac}=3V_{an}\).

  • \[\begin{aligned} V_{an}&=\dfrac{q_a}{2\pi\epsilon}~ln \dfrac{D}{r} \\ C_{n}&=\dfrac{q_a}{V_{an}}=\dfrac{2\pi\epsilon}{ln(D/r)}~F/m \end{aligned}\]
    On substitution,
  • \[I_{chg} = j \omega C_{ab}V_{ab}\]
    line, the charging currentFor
  • \[I_{chg} = j \omega C_{n}V_{an}\]
    line, the charging current per phaseFor

Capacitance of a three-phase line with unsymmetrical spacing

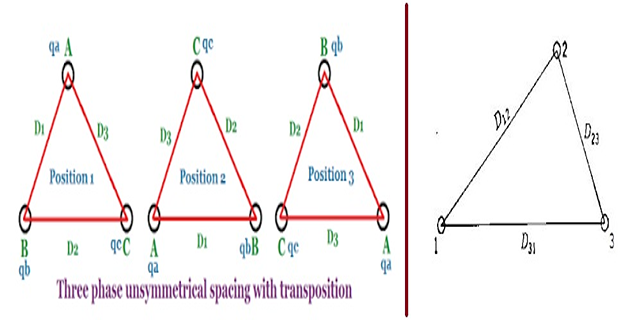
image
  • \[V_{ab}=\dfrac{1}{2\pi\varepsilon}\left(q_{a}ln\dfrac{D_{12}}{r}+q_{b}ln\dfrac{r}{D_{12}}+q_{c}ln\dfrac{D_{23}}{D_{31}}\right)~V\]
    in position 3, in position 2, and in position 1, With phase
  • \[V_{ab}=\dfrac{1}{2\pi\varepsilon}\left(q_{a}ln\dfrac{D_{23}}{r}+q_{b}ln\dfrac{r}{D_{23}}+q_{c}ln\dfrac{D_{31}}{D_{12}}\right)~V\]
    in position 1, in position 3, and in position 2, With phase

  • With phase \(a\) in position 3, \(b\) in position 1, and \(c\) in position 2,

    \[V_{ab}=\dfrac{1}{2\pi\varepsilon}\left(q_{a}ln\dfrac{D_{31}}{r}+q_{b}ln\dfrac{r}{D_{31}}+q_{c}ln\dfrac{D_{12}}{D_{23}}\right)V\]
  • \[\begin{aligned} V_{ab} & =\dfrac{1}{6\pi\varepsilon}\left(q_{a}ln\dfrac{D_{12}D_{23}D_{31}}{r^{3}}+q_{b}ln\dfrac{r^{3}}{D_{12}D_{23}D_{31}}+q_{c}ln\dfrac{D_{12}D_{23}D_{31}}{D_{12}D_{23}D_{31}}\right)\\ & =\dfrac{1}{2\pi\varepsilon}\left(qln\dfrac{D_{eq}}{r}+qln\dfrac{r}{D_{eq}}\right) \end{aligned}\]
    The average voltage drop

    where \(D_{eq} = \sqrt[3]{D_{12}D_{23}D_{31}}\)

  • \[\begin{aligned} V_{ac} & =\dfrac{1}{2\pi\varepsilon}\left(q_{a}ln\dfrac{D_{eq}}{r}+q_{c}ln\dfrac{r}{D_{eq}}\right)V \end{aligned}\]
    The average voltage drop
  • \[3V_{an}=V_{ab}+V_{ac}=\dfrac{1}{2\pi\varepsilon}\left(2q_{a}ln\dfrac{D_{eq}}{r}+q_{b}ln\dfrac{r}{D_{eq}}+q_{c}ln\dfrac{r}{D_{eq}}\right)V\]
    The voltage to neutral
    \[V_{an}=\dfrac{1}{2\pi\varepsilon}q_{a}ln\dfrac{D_{eq}}{r}V\]
    Since,

    equation* C_n==F/m