Bus Impedance Matrix (Zbus) in Power Systems
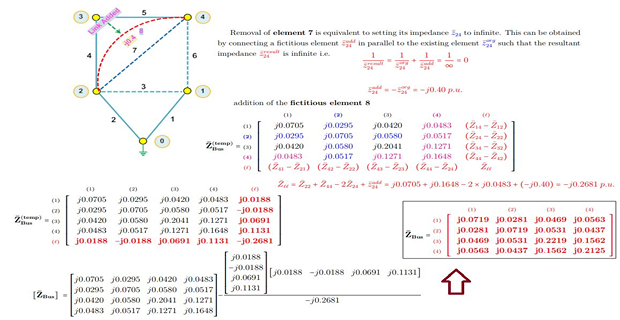
Demonstrative Video
Bus Impedance Matrix
Bus impedance matrix and its relationship with bus voltages & Currents \[\begin{aligned} \mathrm{Z_{bus}} & = \mathrm{Y_{bus}^{-1}} \\ \mathrm{V} & = \mathrm{Z_{bus}} \cdot \mathrm{I} \end{aligned}\]
\(\mathrm{Z_{bus}}\) is also symmetrical similar to \(\mathrm{Y_{bus}}\) around the principal diagonal
Elements on the main diagonal are called driving point impedances of the buses
Off diagonal elements are called transfer impedances of the buses
\(\mathrm{Z_{bus}}\) is very useful in fault analysis
Formulation of Bus Impedance Matrix
\(\mathrm{Z_{bus}}\) can be determined by two methods:
Determine \(\mathrm{Y_{bus}}\) and take its inverse
Directly formed from reactance diagram which requires knowledge of modification of existing \(\mathrm{Z_{bus}}\) matrix due to addition of new buses or addition of new line (or impedances) between existing buses
\(Z_{Bus}\) Building Algorithm
Step-by-step technique which proceeds branch by branch.
Advantage that any modification of the network does not require complete rebuilding of \(\mathrm{Z_{bus}}\) formulation \[\mathrm{Z_{BUS}\left(old\right)\ \underrightarrow{Z_{b}=\text{branch impedance}}}\ \mathrm{Z_{Bus}\left(new\right)}\]
Upon adding a new branch, one of the following situations is presented
Type-1 modification: \(Z_b\) is added from a new bus to the reference bus
Type-2 modification: \(Z_b\) is added from a new bus to an old bus
Type-3 modification: \(Z_b\) connects an old bus to the reference branch
Type-4 modification: \(Z_b\) connects two old buses
\(Z_b\) connects two new buses
\(\mathrm{Z_{BUS}}\) remains unaffected in this case, situation can be avoided
Type-1 Modification
\(\checkmark\) Adding \(Z_b\) from new bus-p \(\rightarrow\) reference bus
\[Z_{\text{bus, new}}=\left[\begin{array}{cccc|c}
& & & & 0\\
& Z_{\text{orig}} & & & 0\\
& & & & \vdots\\
& & & & 0\\
\hline 0 & 0 & \cdots & 0 & Z_{b}
\end{array}\right]\]
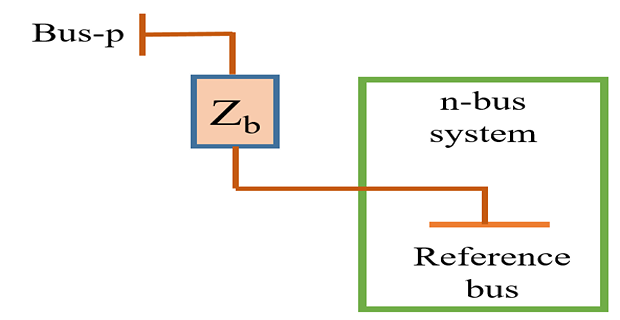
dimension of \(\mathrm{Z_{BUS}}\) goes up by one
\((n+1)^{th}\) column and row are all zeros except the diagonal element
Type-2 Modification
\(\checkmark\) Adding \(Z_b\) from new bus-p \(\rightarrow\) existing bus-q
\[
Z_{\text{bus, new}}=\left[\begin{array}{cccc|c}
& & & & Z_{1q}\\
& Z_{\text{orig}} & & & Z_{2q}\\
& & & & \vdots\\
& & & & Z_{nq}\\
\hline Z_{q1} & Z_{q2} & \cdots & Z_{qn} & Z_{qq}+Z_{b}
\end{array}\right]
\]
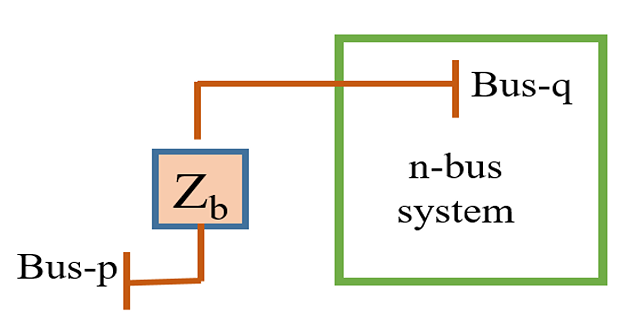
dimension of \(\mathrm{Z_{BUS}}\) goes up by one
elements of \((n+1)^{th}\) column are the elements of \(q^{th}\) column and elements of \((n+1)^{th}\) row are the elements \(q^{th}\) row
Type-3 Modification
\(\checkmark\) Adding \(Z_b\) from existing bus-q \(\rightarrow\) reference bus
a new loop is formed but the dimension of \(\mathrm{Z_{BUS}}\) does not change
\[Z_{jk,act}=Z_{jk}-\dfrac{Z_{j\left(n+1\right)}Z_{\left(n+1\right)k}}{Z_{\left(n+1\right)\left(n+1\right)}}\]
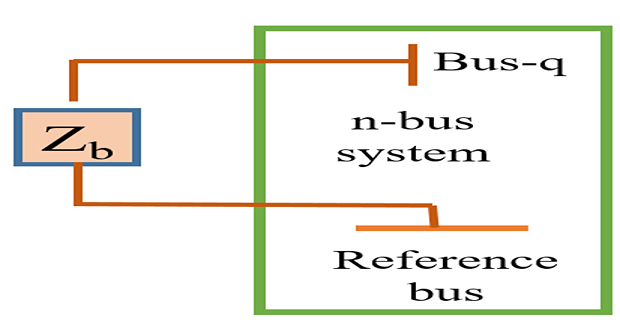
\(Z_{jk,act}\) corresponding to row-j and column-k of actual new \(Z_{bus}\)
\(Z_{jk}\), \(Z_{(n+1)k}\), \(Z_{j(n+1)}\), \(Z_{(n+1)(n+1)}\) impedances of new \(Z_{bus}\) or order \((n+1)\)
\(Z_{jk,act} = Z_{kj,act}\)
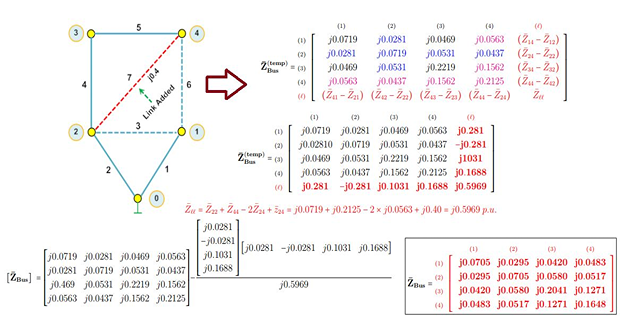
Type-4 Modification
\(\checkmark\) Adding \(Z_b\) between two existing buses h and q
new loop is formed but the dimension of \(\mathrm{Z_{BUS}}\) does not change
\[ Z_{\text{bus, new}}=\left[\begin{array}{cccc|c} & & & & Z_{1h}-Z_{1q}\\ & Z_{\text{orig}} & & & Z_{2h}-Z_{2q}\\ & & & & \vdots\\ & & & & Z_{nh}-Z_{nq}\\ \hline Z_{h1}-Z_{q1} & Z_{h2}-Z_{q2} & \cdots & Z_{hn}-Z_{qn} & Z_{\left(n+1\right)\left(n+1\right)} \end{array}\right] \] \[Z_{\left(n+1\right)\left(n+1\right)}=Z_{b}+Z_{hh}+Z_{qq}-2Z_{hq}\]
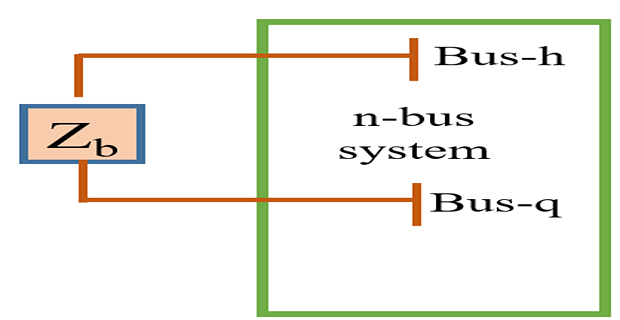
elements of \((n+1)^{th}\) column is the difference between the elements of column-h and column-q
elements of \((n+1)^{th}\) row is the difference between the elements of row-h and row-q
No new bus is involved so reduced the size of matrix to \((n \times n)\) \[\Rightarrow ~ Z_{jk,act}=Z_{jk}-\dfrac{Z_{j\left(n+1\right)}Z_{\left(n+1\right)k}}{Z_{\left(n+1\right)\left(n+1\right)}}\]
\(Z_{Bus}\) Formulation
What is the size of \(Z_{Bus}\) ?
Can we directly find \(Z_{Bus}\) from \(Y_{Bus}\)?
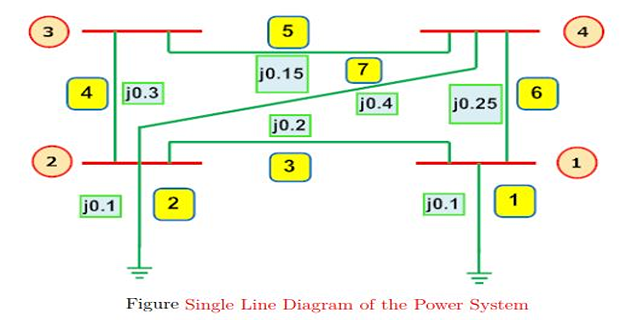
Step-by-Step procedure for \(Z_{Bus}\) formulation
No closed path should be there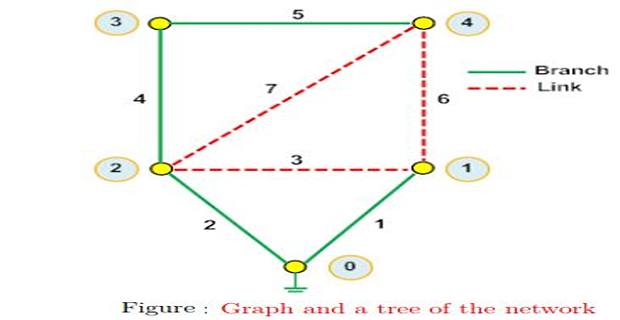 
Step-1
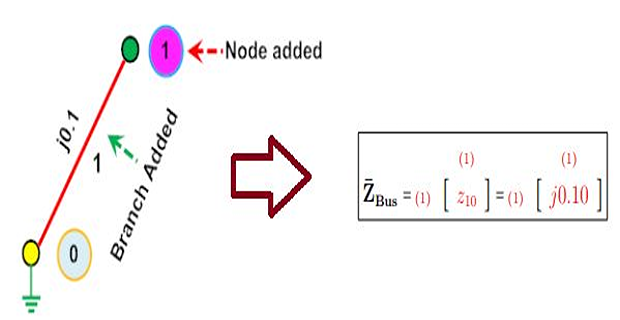
Step-2
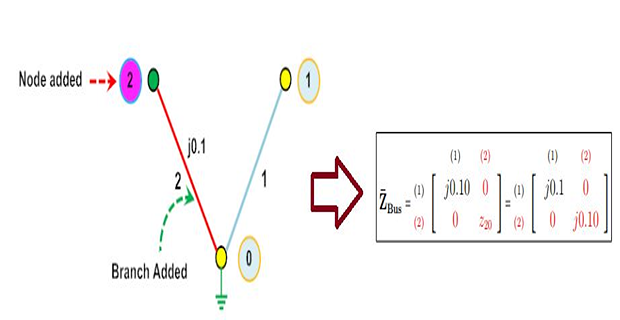
Step-3
Step-4
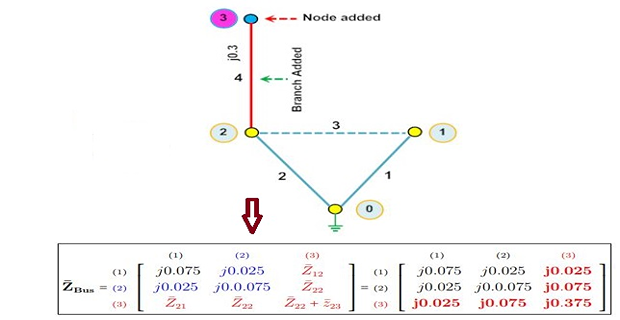
Step-5
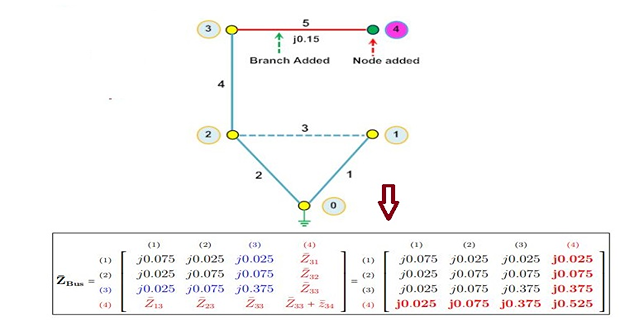
Step-6
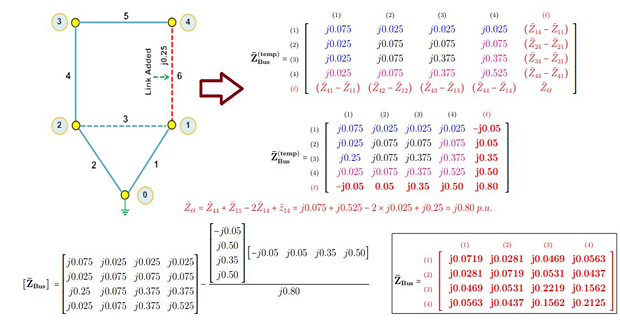
Step-7
Modification of the existing \(Z_{Bus}\)
