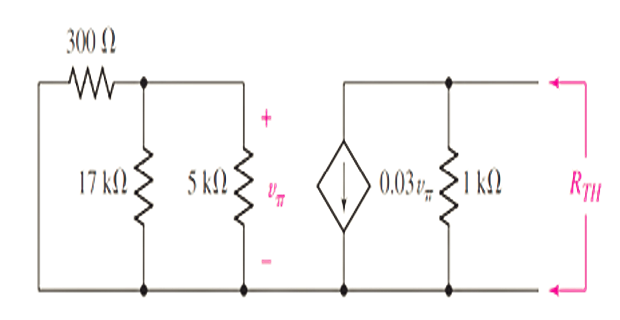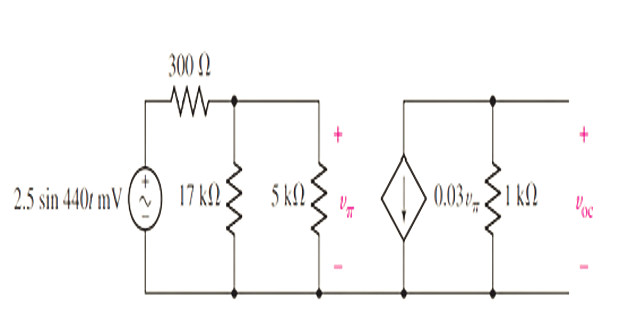Solved Problem of AC Circuit Using Theorems in Frequency Domain

Demonstrative Video

Contents

Fundamentals
Voltage Division
Current Division

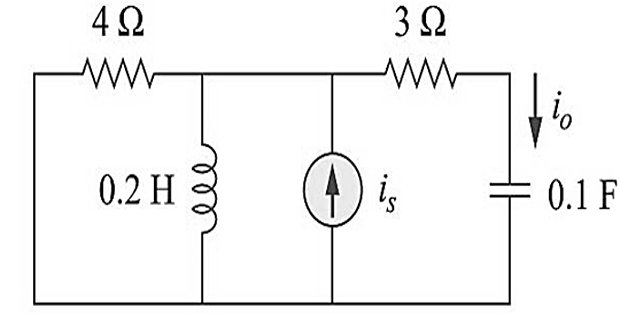
Problem-1

  • If \(i_s = 5\cos(10t+40^{\circ})\) A then determine \(i_0\).

image

Solution-1

\[\begin{aligned} \mathrm{i}_{\mathrm{s}}=& 5 \cos \left(10 \mathrm{t}+40^{\circ}\right)\\ \rightarrow & \mathbf{I}_{\mathrm{s}}=5 \angle 40^{\circ} \\ & 0.1 \mathrm{~F} \longrightarrow \frac{1}{j \omega \mathrm{C}}\\ &=\frac{1}{j(10)(0.1)}=-j \\ 0.2 \mathrm{H} & \longrightarrow \quad j \omega \mathrm{L}\\ &=j(10)(0.2)=j 2 \end{aligned}\]
\[\begin{aligned} &\mathbf{Z}_{1}=4 \| \mathrm{j} 2=\frac{\mathrm{j} 8}{4+\mathrm{j} 2}=0.8+\mathrm{j} 1.6 \qquad \mathbf{Z}_{2}=3-\mathrm{j} \\ &\mathbf{I}_{\mathrm{o}}=\frac{\mathbf{Z}_{1}}{\mathbf{Z}_{1}+\mathbf{Z}_{2}} \mathbf{I}_{\mathrm{s}}=\frac{0.8+\mathrm{j} 1.6}{3.8+\mathrm{j} 0.6}\left(5 \angle 40^{\circ}\right) \\ &\mathbf{I}_{\mathrm{o}}=\frac{\left(1.789 \angle 63.43^{\circ}\right)\left(5 \angle 40^{\circ}\right)}{3.847 \angle 8.97^{\circ}}=2.325 \angle 94.46^{\circ} \\ &\mathrm{i}_{\mathrm{o}}(\mathrm{t})=\underline{\mathbf{2 . 3 2 5} \cos \left(\mathbf{1 0} \mathbf{t}+\mathbf{9 4 . 4 6}^{\circ}\right) \mathbf{A}} \end{aligned}\]

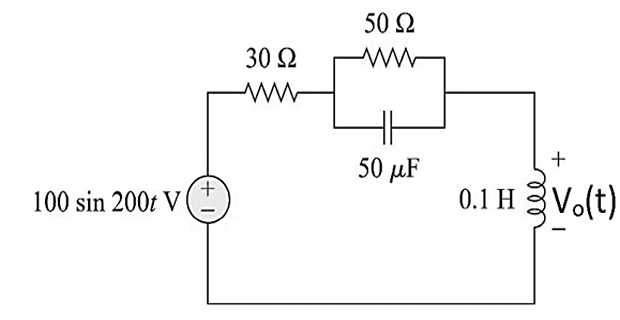
Problem-2

  • Calculate \(V_0(t)\) in the given figure?

image

Solution-2

\[\begin{aligned} & \omega=200 \\ & 50 \mu \mathrm{F} \longrightarrow \frac{1}{\mathrm{j} \omega \mathrm{C}}=\frac{1}{\mathrm{j}(200)\left(50 \times 10^{-6}\right)}\\ & \quad =-\mathrm{j} 100 \\ & 0.1~\mathrm{H} \longrightarrow j\omega L \\ & \quad = j(200)(0.1) = j20 \end{aligned}\]
\[\begin{gathered} 50 \|-\mathrm{j} 100=\frac{(50)(-\mathrm{j} 100)}{50-\mathrm{j} 100}=\frac{-\mathrm{j} 100}{1-\mathrm{j} 2}=40-\mathrm{j} 20 \\ \mathbf{V}_{\mathrm{o}}=\frac{\mathrm{j} 20}{\mathrm{j} 20+30+40-\mathrm{j} 20}\left(60 \angle 0^{\circ}\right)=\frac{\mathrm{j} 20}{70}\left(60 \angle 0^{\circ}\right)=17.14 \angle 90^{\circ} \\ \mathrm{v}_{\mathrm{o}}(\mathrm{t})=\underline{\mathbf{1 7 . 1 4} \sin \left(\mathbf{2 0 0} \mathbf{t}+\mathbf{9 0}^{\circ}\right) \mathbf{V}} \\ \text { or } \mathrm{v}_{\mathrm{o}}(\mathrm{t})=\underline{\mathbf{1 7 . 1 4} \cos (\mathbf{2 0 0 t}) \mathbf{V}} \end{gathered}\]

KCL and KVL
Mesh Analysis
Nodal Analysis

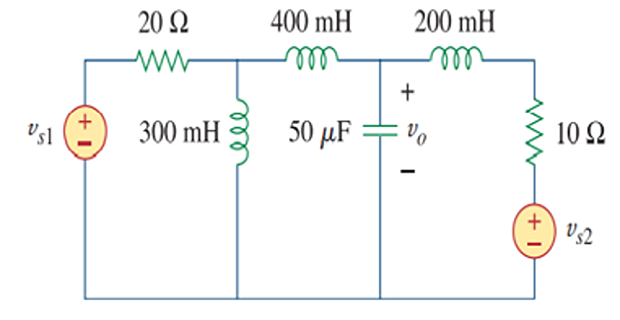
Problem-3

  • Use mesh analysis to find \(v_0\) if \(V_{s1} = 120\cos (100t+90)\) V and \(V_{s2} =80 \cos 100t\) V.

image

Solution-3

\[\begin{array}{ll} 300 \mathrm{mH} & \longrightarrow j \omega L=j 100 \times 300 \times 10^{-3}=j 30 \\ 200 \mathrm{mH} & \longrightarrow j \omega L=j 100 \times 200 \times 10^{-3}=j 20 \\ 400 \mathrm{mH} & \longrightarrow j \omega L=j 100 \times 400 \times 10^{-3}=j 40 \\ 50 \mu \mathrm{F} & \longrightarrow 1 / j \omega \mathrm{C}=\frac{1}{j 100 \times 50 \times 10^{-6}}=-j 200 \end{array}\]
\[\begin{aligned} \text{Mesh-1} \Rightarrow & -120\angle 90^{\circ}+(20+j30)I_1-j30I_2=0 \\ \text{Mesh-2} \Rightarrow & -j30+(j30+j40-j200)I_2+j200I_3=0\\ \text{Mesh-3} \Rightarrow & 80+j200I_2+(10-j180)I_3=0 \end{aligned}\]
\[\left[\begin{array}{ccc} 2+\mathrm{j} 3 & -\mathrm{j} 3 & 0 \\ -3 & -13 & 20 \\ 0 & \mathrm{j} 20 & 1-\mathrm{j} 18 \end{array}\right]\left[\begin{array}{c} \mathrm{I}_{1} \\ \mathrm{I}_{2} \\ \mathrm{I}_{3} \end{array}\right]=\left[\begin{array}{c} \mathrm{j} 12 \\ 0 \\ -8 \end{array}\right]\]

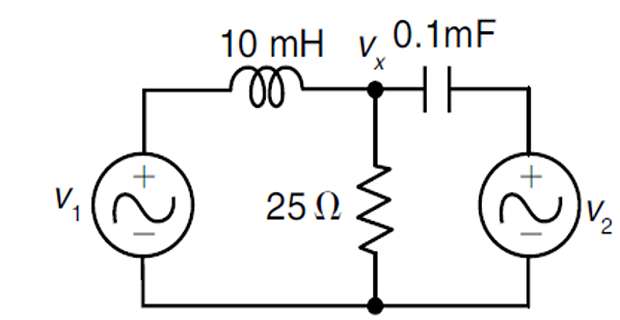
Problem-4

  • Find \(V_x\) if \(V_1(t)=20\cos 1000t\) V and \(V_2(t)=20\sin 1000t\)

image

Solution-4

\[\begin{aligned} \omega & = 10^3~\text{rad/s} \\ X_L & = j\omega L = j10~\Omega \\ X_C & = \dfrac{-j}{\omega C} = -j10~\Omega\\ V_1 & = 20\angle 0^{\circ} \quad V_2 = 20\angle -90^{\circ} \end{aligned}\]
\[\begin{aligned} &\Rightarrow V_{x}\left[\frac{1}{j 10}-\frac{1}{j 10}+\frac{1}{25}\right]=\frac{20}{j 10} \angle 0^{\circ}-\frac{20}{j 10} \angle-90^{\circ} \\ &\Rightarrow \frac{V_{x}}{25}=(2-j 2) \Rightarrow V_{x}=50-j 50=70.71 \angle-45^{\circ}(\mathrm{V}) \\ &\therefore v_{x}(t)=70.71 \cos \left(1000 t-45^{\circ}\right)(\mathrm{V}) \end{aligned}\]
KCL at node

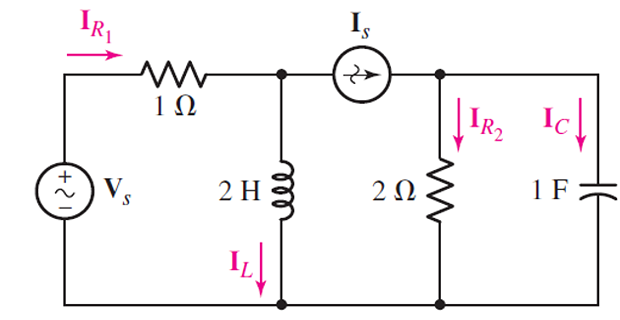
Problem-5

  • Determine \(I_{R2}(t)\) and \(I_s(t)\), if both sources operate at \(\omega = 2\) rad/sec and \(I_c=2\angle 28^{\circ}\).

image

Solution-5

\[\begin{aligned} V_c & = \dfrac{1}{j\omega C} I_c = 1\angle -62^{\circ}~\mathrm{V}\\ I_{R2} & = \dfrac{V_c}{2} = 0.5 \angle -62^{\circ}~\mathrm{A}\\ I_s & = I_{R2}+I_c = 1.5\angle -62^{\circ}~\mathrm{A}\\ \end{aligned}\]
\[\begin{aligned} i_s(t) &= 1.5 \cos (2t-62^{\circ})~\mathrm{A} \end{aligned}\]

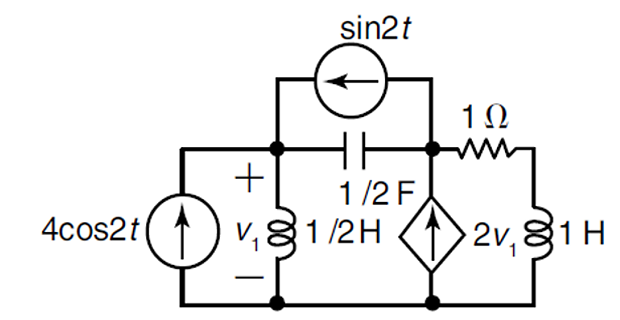
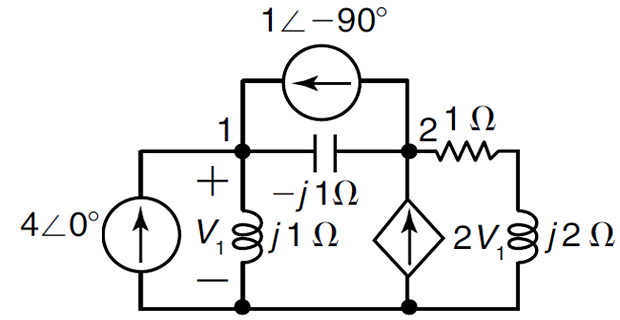
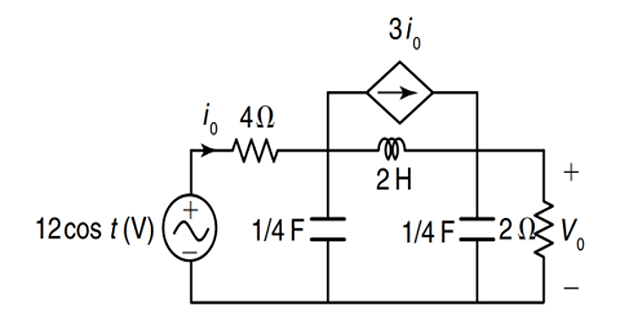
Problem-6

  • Determine \(v_1\) ?

image

Solution-6

image
\[\begin{aligned} \omega & =2~\text{rad/sec},~L_1 = 0.5~\text{H}~L_2 = 1~\text{H}~C = 0.5~\text{F}\\ X_{L1} & = j1~\Omega, ~X_{L2} = j2~\Omega, ~X_{c} = -j1~\Omega, ~ \end{aligned}\]
On solving:

Thevenin’s Theorem
Norton’s Theorem

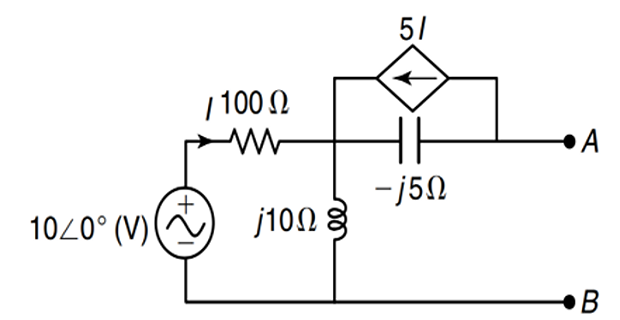
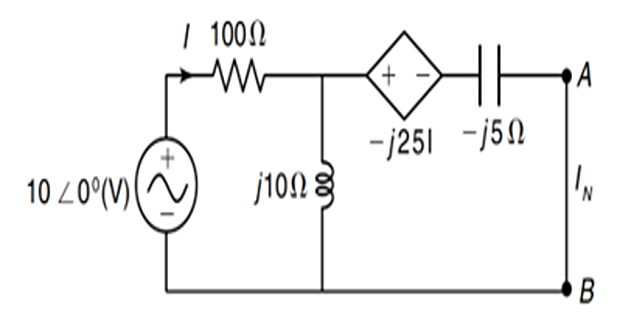
Problem-7

  • Find Thevenin’s equivalence with respect to terminals A-B as shown in the below circuit?

image

Solution-7

image
\[\begin{aligned} I & = \dfrac{10\angle 0^{\circ}}{100+j10} \\ &= 0.09995\angle -5.7^{\circ}~\mathrm{A}\\ V_{Th}&=V_{AB} \\ &= \left(I\times j 10\right)-\left(5I\times (-j5)\right)\\ & = 3.48\angle 84.3^{\circ} ~\mathrm{V} \end{aligned}\]

Problem-8

  • Find \(V_0\) using Thevenin’s theorem ?

image

Solution-8

\[\begin{aligned} 2~\Omega & \Rightarrow \text{open} \\ i_0 & = I_1 \\ \text{KVL-1} & ~(4-j4)I_1+j4I_2 = -12 \\ \text{KVL-2} & ~-j2I_1+(-j6)I_2 = 0\\ \text{Solving} ~ I_2 & = 0.6\angle 53.13^{\circ} ~\mathrm{A} \\ V_{Th} & = I_2 \times (-j8) \\ & = 4.8\angle -36.87^{\circ} ~\mathrm{V} \end{aligned}\]
\[\begin{aligned} 2~\Omega & \Rightarrow \text{short and dep. source transformation} \\ \text{KVL} ~& (4-j4)I_1+j4I_2 = -12\\ \text{Solving} ~I_2 & = I_N = 1.34\angle 63.43^{\circ} \\ Z_{TH} & = \dfrac{V_{TH}}{I_N} = 3.58\angle -100.3^{\circ}~\Omega \\ v_0 & = \left(\dfrac{V_{TH}}{Z_{TH}+2}\right) \times 2 = 1.27 \angle 32^{\circ} \end{aligned}\]

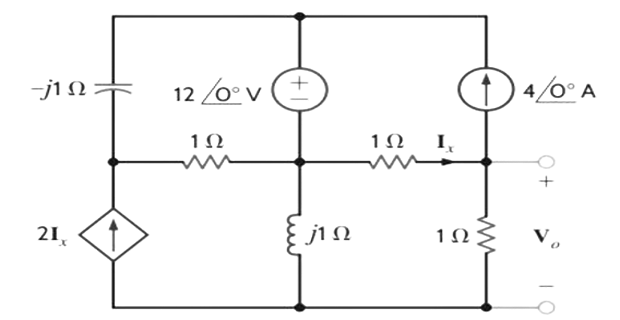
Problem-9

  • Find voltage \(V_0\) across \(1~\Omega\) resistor ?

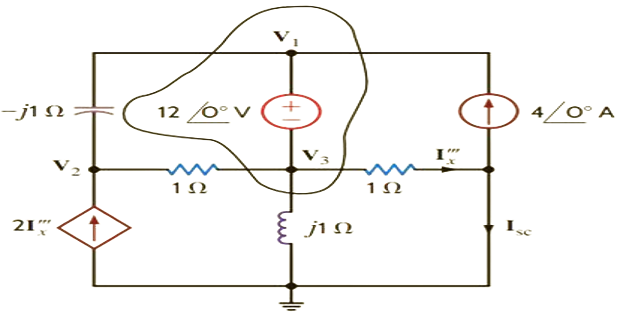
image

Solution-9

image
\[\begin{aligned} \mathbf{V}_{3}+12 \angle 0^{\circ} &=\mathbf{V}_{1} \\ \frac{\mathbf{V}_{2}-\mathbf{V}_{1}}{-j 1}+\frac{\mathbf{V}_{2}-\mathbf{V}_{3}}{1}-2 \mathbf{I}_{x}^{\prime \prime \prime} &=0 \\ \frac{\mathbf{V}_{1}-\mathbf{V}_{2}}{-j 1}+\frac{\mathbf{V}_{3}-\mathbf{V}_{2}}{1}-4 \angle 0^{\circ}+\frac{\mathbf{V}_{3}}{j 1}+\mathbf{I}_{x}^{\prime \prime \prime} &=0 \\ \mathbf{I}_{x}^{\prime \prime \prime} &=\frac{\mathbf{V}_{3}}{1} \end{aligned}\]
\[\left[\begin{array}{cccc} -1 & 0 & 1 & 0 \\ -\mathrm{j} & (1+\mathrm{j}) & -1 & -2 \\ \mathrm{j} & -(1+\mathrm{j}) & 1-\mathrm{j} & 1 \\ 0 & 0 & -1 & 1 \end{array}\right]\left[\begin{array}{c} \mathbf{V}_{1} \\ \mathbf{V}_{2} \\ \mathbf{V}_{3} \\ \mathbf{I}_{x}^{\prime \prime \prime} \end{array}\right]=\left[\begin{array}{r} -12 \\ 0 \\ 4 \\ 0 \end{array}\right]\]
\[\begin{aligned} \mathbf{I_x^{'''}}& = 2.8284\angle 135^{\circ}~\mathrm{A} \\ \mathbf{I_x^{'''}}& = 4\angle 0^{\circ} + \mathbf{I_{sc}}\\ \mathbf{I_{sc}}& = 6.3245\angle 161.57^{\circ}~\mathrm{A} \end{aligned}\]
The matrix equation is
\[\begin{aligned} Z_{TH} & = (1-j)~\Omega \\ V_0 & = I_{sc} \left[(1)(1-j)/(1+1-j)\right]~\mathrm{V}\\ & = 4 \angle 143.13^{\circ} ~\mathrm{V} \end{aligned}\]

Source Transformation

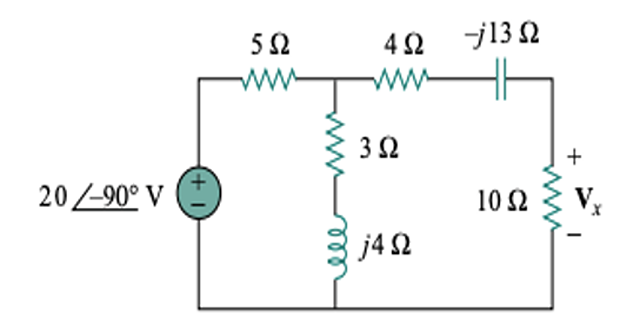
Problem-10

  • Calculate \(V_x\) using the method of source Transformation.

image

Solution-10

image
\[\mathbf{I}_{s}=\frac{20 \angle -90^{\circ}}{5}=4 \angle-90^{\circ}=-j 4 \mathrm{~A}\]
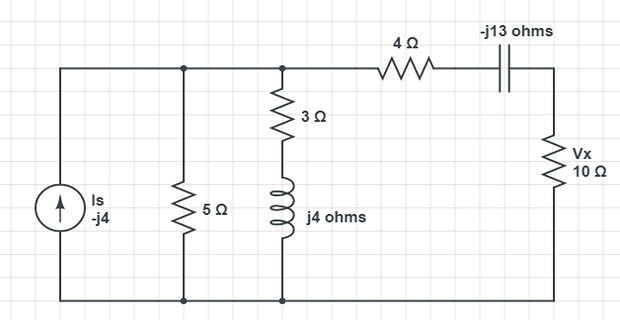
\[\mathbf{Z}_{1}=\frac{5(3+j 4)}{8+j 4}=2.5+j 1.25 \Omega\]
\((3+j 4)\)\(5-\Omega\)Transform the voltage source to a current source
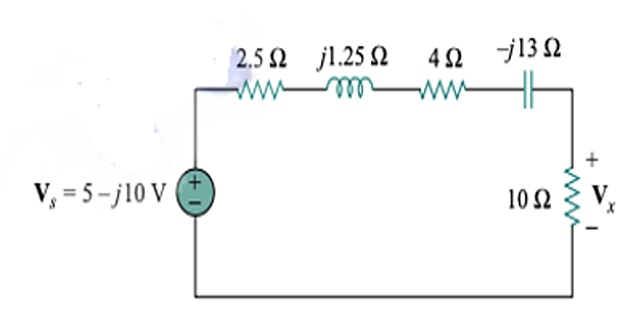
image
\[\mathbf{V}_{s}=\mathbf{I}_{s} \mathbf{Z}_{1}=-j 4(2.5+j 1.25)=5-j 10 \mathrm{~V}\]
\[\mathbf{V}_{x}=\frac{10}{10+2.5+j 1.25+4-j 13}(5-j 10)=5.519 \angle-28^{\circ} \mathrm{V}\]
Converting the current source to a voltage source

Maximum Power Transfer Theorem

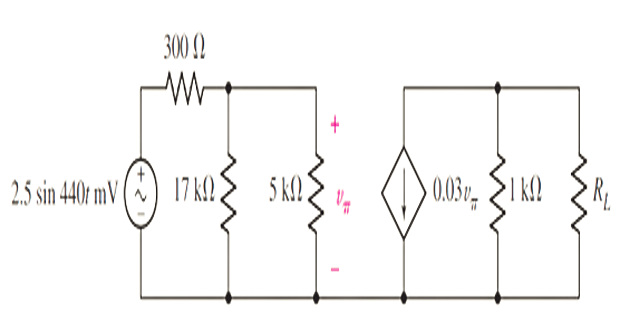
Problem-11

  • Choose a load resistance so that maximum power is transferred to it and calculate the actual power transferred?

image

Solution-11

image

  • Since \(v_{\pi}=0\), the dependent current source is an open circuit, and \(R_{T H}=1 \mathrm{k} \Omega\). This can be verified by connecting an independent \(1 \mathrm{~A}\) current source across the \(1 \mathrm{k} \Omega\) resistor; \(v_{\pi}\) will still be zero, so the dependent source remains inactive and hence contributes nothing to \(R_{T H}\).

image
  • \[v_{\mathrm{oc}}=-0.03 v_{\pi}(1000)=-30 v_{\pi}\]
    \[p_{\max }=\frac{v_{T H}^{2}}{4 R_{T H}}=1.211 \sin ^{2} 440 t \mu \mathrm{W}\]
    \(1 \mathrm{k} \Omega\)\(-69.6 \sin 440 t \mathrm{mV}\)
    \[v_{\pi}=\left(2.5 \times 10^{-3} \sin 440 t\right)\left(\frac{3864}{300+3864}\right)\]
    \(v_{\pi}\). should be set to In order to obtain maximum power delivered into the load,

Problem-12

  • A loudspeaker is connected across terminals A and B of the network. What should its impedance be to obtain maximum power dissipation in it?

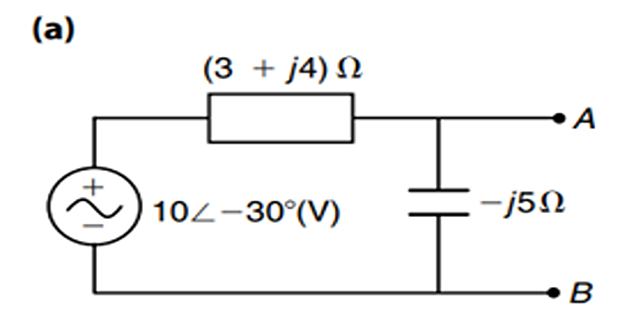
image
image

Solution-12

  1. \[Z_{\text {th }}=\frac{(3+j 4)(-j 5)}{3+j 4-j 5}=7.9 \angle-18.43^{\circ} \Omega=(7.5-j 2.5) \Omega\]
    \(Z_{L}=Z_{\text {th }} *=(7.5+j 2.4) \Omega\) is and Equivalent impedance with respect to the terminals
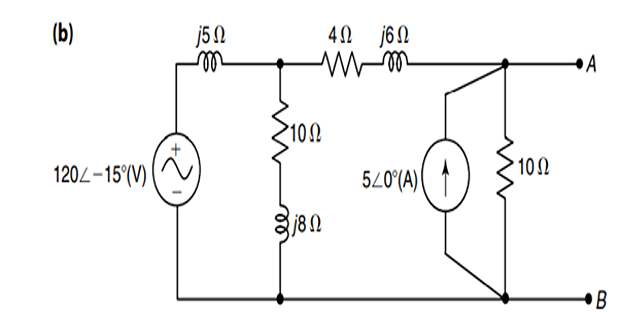
  1. \[\begin{aligned} Z_{\mathrm{th}} &=\left[\frac{(10+j 8) j 5}{10+j 8+j 5}+4+j 6\right]|| 10\\ &=\left(\frac{-40+j 50+40+j 52+j 60-78}{10+j 13}\right)|| 10 \\ &=6.14 \angle 30^{\circ} \Omega=(5.316+j 3.07) \Omega \end{aligned}\]
    \(Z_{L}=Z_{\text {th }} *=6.14 \angle-30^{\circ} \Omega=(5.316-j 3.07) \Omega\) is and Equivalent impedance with respect to the terminals

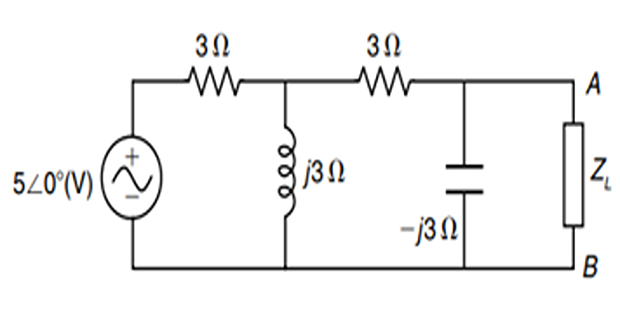
Problem-13

  • In the network shown, find the value of \(Z_L\) to which the maximum power can be delivered. Hence, find the value of the maximum power?

image

Solution-13

  • \[V_{\mathrm{th}}=\frac{5 \angle 0^{\circ}}{3+\frac{j 3(3-j 3)}{3-j 3+j 3}} \times\left(\frac{j 3}{3+j 3-j 3}\right)=\frac{45 \angle 0^{\circ}}{18+j 9}=2.236 \angle-26.56^{\circ}(\mathrm{V})\]
    , the Thevenin voltage is and With respect to terminals

  • Thevenin impedance, \(Z_{\mathrm{h}}=\frac{\left(3+\frac{3 \times j 3}{3+j 3}\right) \times(-j 3)}{3+\frac{3 \times j 3}{3+j 3}-j 3}=3 \angle-53.12^{\circ} \Omega=(1.8-j 2.4) \Omega\)

  • For maximum power transfer, \(Z_{L}=Z_{\text {th }}{ }^{*}=(1.8+j 2.4) \Omega\)

  • Current, \(I=\frac{2.236 \angle-26.56^{\circ}}{1.8 \times 2}=0.621 \angle-26.56^{\circ} \mathrm{A}\)

  • The value of the maximum power is, \(P_{\max }=\frac{\left(V_{\text {th }}\right)^{2}}{4 R}=\frac{(2.236)^{2}}{4 \times 1.8}=0.694 \mathrm{~W}\)