Solved Problems on Superposition Theorem

Demonstrative Video

Problem-1

Solution-1

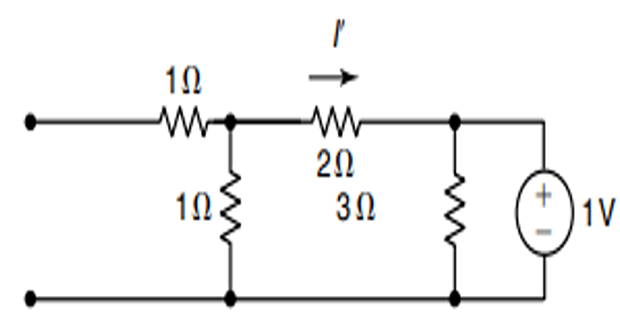
image

  • When voltage source acting alone \(I^{'} = -1/3\) A

  • When current source is acting alone

    \[I^{''} = 1\times \dfrac{1}{1+2}=1/3~\mathrm{A}\]
  • \[I=(I^{'}+I^{''}) = -1/3+1/3=0\]
    By Superposition:

Problem-2

  • Use superposition theorem to determine current \(I\) ?

    image

Solution-2

To determine the current \(I\), we analyze the contribution of each independent source while keeping the dependent source active in both cases.

Step 1: 10V Source Active (2A Source Deactivated)

Replace the 2A current source with an open circuit. The circuit becomes a single series loop. Let the current be \(I_1\).

Since \(V_x\) is the voltage across the \(2\Omega\) resistor:

\[ V_{x1} = 2I_1 \]

Applying Kirchhoff’s Voltage Law (KVL):

\[ -10 + 5I_1 - 2V_{x1} + 2I_1 = 0 \]

Substituting \(V_{x1}\):

\[ -10 + 5I_1 - 2(2I_1) + 2I_1 = 0 \] \[ -10 + 5I_1 - 4I_1 + 2I_1 = 0 \] \[ 3I_1 = 10 \implies I_1 = \frac{10}{3} \text{ A} \]

Step 2: 2A Source Active (10V Source Deactivated)

Replace the 10V voltage source with a short circuit. Let the current contribution be \(I_2\) and the node voltage be \(V_{x2}\).

Applying Kirchhoff’s Current Law (KCL) at the top node:

\[ \frac{V_{x2} - 2V_{x2}}{5} + \frac{V_{x2}}{2} - 2 = 0 \]

Multiplying by 10 to clear fractions:

\[ 2(V_{x2} - 2V_{x2}) + 5V_{x2} = 20 \] \[ -2V_{x2} + 5V_{x2} = 20 \implies 3V_{x2} = 20 \implies V_{x2} = \frac{20}{3} \text{ V} \]

Finding \(I_2\) through the \(5\Omega\) branch:

\[ I_2 = \frac{0 - (V_{x2} - 2V_{x2})}{5} = \frac{V_{x2}}{5} = \frac{20/3}{5} = \frac{4}{3} \text{ A} \]

Final Calculation

Summing the individual contributions:

\[ I = I_1 + I_2 \] \[ I = \frac{10}{3} + \frac{4}{3} = \frac{14}{3} \text{ A} \]

Total Current: \( I \approx 4.67 \text{ A} \)

Problem-3

  • Find \(i_0\) and \(i\) using Superposition ?

    image

Solution-3

  • \[\begin{aligned} i^{'}_0 & = i^{'} \\ \text{KVL} \Rightarrow & 6i^{'}+2i^{'}=6\\ \Rightarrow & i^{'} = i^{'}_0=0.75~\mathrm{A} \end{aligned}\]
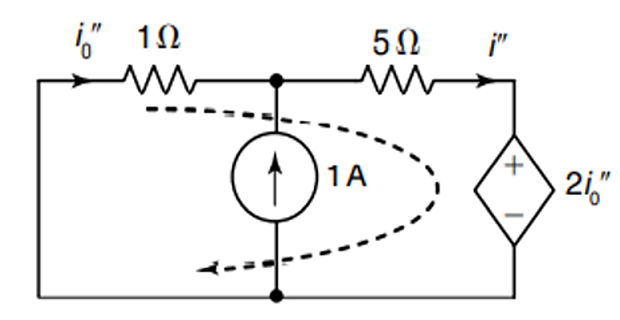
    image
    When 6-V source acting alone
image

  • When 1-A current source is acting alone

    \[\begin{aligned} \text{KCL} \Rightarrow 1&=i^{\prime \prime}-i_{0}^{\prime \prime} \Rightarrow i^{\prime \prime}=1+i_{0}^{\prime \prime} \\ \text{KVL in supermesh} \Rightarrow & 1 \times i_{0}^{\prime \prime}+5 i^{\prime \prime}+2 i_{0}^{\prime \prime}=0\\ & 3 i_{0}^{\prime \prime}+5 i^{\prime \prime}=0\\ & 3 i_{0}^{\prime \prime}+5\left(1+i_{0}^{\prime \prime}\right)=0\\ & i_{0}^{\prime \prime}=-\frac{5}{4}=-1.25 \mathrm{~A}\\ \therefore ~ & i^{\prime \prime}=1-1.25=-0.25 \mathrm{~A} \end{aligned}\]

  • By superposition:

    \[\left.\begin{array}{l} i=\left(i^{\prime}+i^{\prime \prime}\right)=(0.75-0.25)=0.5 \mathrm{~A} \\ i_{0}=\left(i_{0}^{\prime}+i_{0}^{\prime \prime}\right)=(0.75-1.25)=-0.5 \mathrm{~A} \end{array}\right\}\]

Problem-4

  • Find \(V_{AB}\) using Superposition theorem ?

    image

Solution-4

  • \[\begin{aligned} I^{\prime} & = 2/12 = 1/6~\mathrm{A} \\ V^{\prime}_{AB} & = I^{\prime} \times 6 = 1~\mathrm{V} \end{aligned}\]
    When 2-V source acting alone

  • When 4-V source acting alone

    \[\begin{aligned} I^{''} & = 4/12 = 1/3~\mathrm{A} \\ V^{''}_{AB} & = I^{''} \times 6 = -2~\mathrm{V} \end{aligned}\]

  • When 2-A source acting alone, convert into equivalent voltage source

    \[\begin{aligned} I^{'''} & = 8/12 = 2/3~\mathrm{A} \\ V^{'''}_{AB} & = - I^{'''} \times 6 = -4~\mathrm{V} \end{aligned}\]
  • \[V_{A B}=V_{A B}^{\prime}+V_{A B}^{\prime \prime}+V_{A B}^{\prime \prime \prime}=(1-2-4)=-5 \mathrm{~V}\]
    By Superposition

Problem-5

  • Determine \(V_1\) using Superposition theorem ?

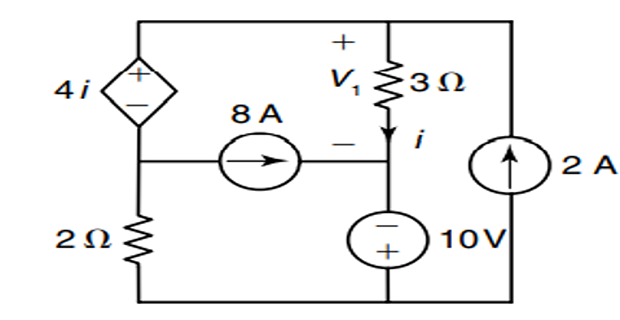
    image

Solution-5

  • When 8-A source is acting alone

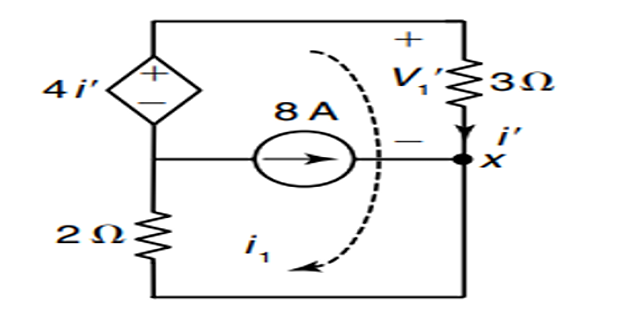
image
\[\begin{aligned} \text{KVL in supermesh} \Rightarrow & 3 i^{\prime}+2 i_{1}-4 i^{\prime}=0 \Rightarrow i_{1}=\frac{1}{2} i^{\prime}\\ \text{KCL at node} x \Rightarrow & i_{1}=\left(8+i^{\prime}\right) \Rightarrow \frac{1}{2} i^{\prime}=8+i^{\prime} \Rightarrow i^{\prime}=-16 \mathrm{~A} \\ \therefore ~ & V_{1}^{\prime}=3 i^{\prime}=3 \times(-16)=-48 \mathrm{~V} \end{aligned}\]

  • When 2-A source is acting alone

image

image

\[\begin{aligned} \text{KVL} \Rightarrow & 3\left(i_{2}+2\right)+2 i_{2}-4 i^{\prime \prime}=0 \Rightarrow 5 i_{2}+6-4 i^{\prime \prime}=0 \\ i^{\prime \prime}&=\left(i_{2}+2\right) \\ &\therefore 5 i_{2}+6-4\left(i_{2}+2\right)=0 \Rightarrow i_{2}=2 \mathrm{~A} \\ &\therefore i^{\prime \prime}=\left(i_{2}+2\right)=(2+2)=4 \mathrm{~A} \\ &\therefore V_{1}^{\prime \prime}=3 i^{\prime \prime}=3 \times 4=12 \mathrm{~V} \end{aligned}\]

  • When 10-V source is acting alone

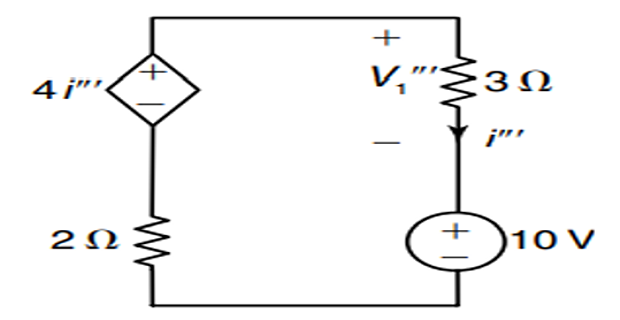
image
  • \[\begin{aligned} &3 i^{\prime \prime \prime}-10+2 i^{\prime \prime \prime}-4 i^{\prime \prime \prime}=0 \Rightarrow i^{\prime \prime \prime}=10 \mathrm{~A} \\ \therefore & V_{1}^{\prime \prime \prime}=10 \times 3=30 \mathrm{~V} \end{aligned}\]
    By KVL,
  • \[V_{1}=\left(V_{1}^{\prime}+V_{1}^{\prime \prime}+V_{1}^{\prime \prime \prime}\right)=(-48+12+30)=-6 \mathrm{~V}\]
    When all the sources are acting simultaneously, by the superposition theorem the voltage is given as

Problem-6

  • Find \(I\) using superposition theorem ?

    image

Solution-6

  • 4-V source alone

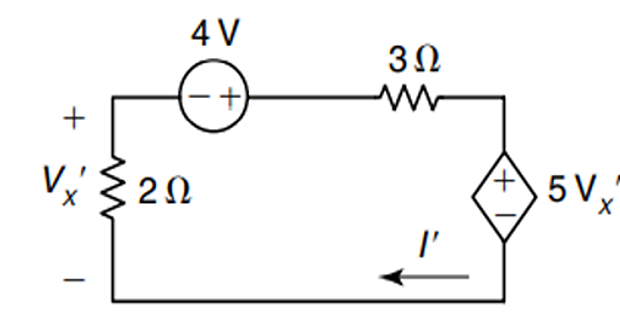
image
\[\begin{aligned} \text{KVL} ~ -4+3 I^{\prime}+5 V_{x}^{\prime}-V_{x}^{\prime} &=0 \\ 3 I^{\prime}+4 \times\left(-2 I^{\prime}\right) &=4 \\ \left[\because V_{x}^{\prime}=-2 I^{\prime}\right] & \end{aligned}\]

’

  • 2-A source alone

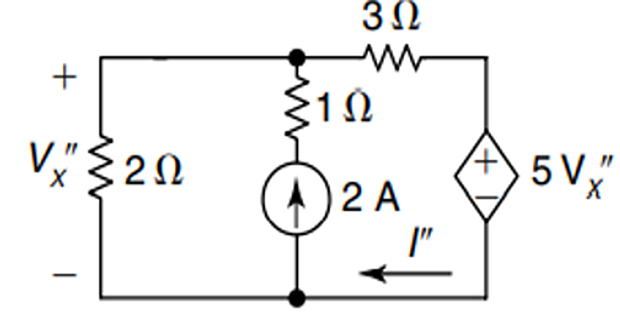
image
\[\begin{aligned} \text {KCL, } & 2=\frac{V_{x}^{\prime \prime}}{2}+\frac{V_{x}^{\prime \prime}-5 V_{x}^{\prime \prime}}{3} \\ & \Rightarrow V_{x}^{\prime \prime}=-\frac{12}{5}=-2.4 \mathrm{~V} \\ \therefore & I^{\prime \prime}=\frac{V_{x}^{\prime \prime}-5 V_{x}^{\prime \prime}}{3} =3.2 \mathrm{~A} \end{aligned}\]

  • \[I=\left(I^{\prime}+I^{\prime \prime}\right)=(-0.8+3.2)=2.4 \mathrm{~A}\]
    By superposition theorem