Master Second-Order Circuits: Conquer Challenges with Solved Problems!

Demonstrative Video

Second-Order Circuits

Response Cases

Overdamped Case \(\left(\alpha>\omega_{0}\right)\) when \(L>4 R^{2} C\)
- The roots of the characteristic equation are real and negative
- \[\boxed{v(t)=A_{1} e^{s_{1} t}+A_{2} e^{s_{2} t}}\]
  The response is
Critically Damped Case \(\left(\alpha=\omega_{0}\right)\) when \(L=4 R^{2} C\)
- The roots are real and equal
- \[\boxed{v(t)=\left(A_{1}+A_{2} t\right) e^{-\alpha t}}\]
  Response:
Underdamped Case \(\left(\alpha<\omega_{0}\right)\) when \(L<4 R^{2} C\)
- \[s_{1,2}=-\alpha \pm j \omega_{d} \quad \left( \omega_{d}=\sqrt{\omega_{0}^{2}-\alpha^{2}}\right)\]
  Roots are complex and may be expressed as
- \[\boxed{v(t)=e^{-\alpha t}\left(A_{1} \cos \omega_{d} t+A_{2} \sin \omega_{d} t\right)}\]
  Response
- \(A_1\) and \(A_2\) are found from initial conditions \(v(0)\) and \(dv(0)/dt\)

Unit Step-function

\[\begin{gathered} u(t)= \begin{cases}0, & t<0 \\ 1, & t>0\end{cases} \\ u\left(t-t_{0}\right)= \begin{cases}0, & t<t_{0} \\ 1, & t>t_{0}\end{cases} \\ u\left(t+t_{0}\right)= \begin{cases}0, & t<-t_{0} \\ 1, & t>-t_{0}\end{cases} \end{gathered}\]

Problem-1

Find \(i(t)\) and \(i_R(t)\) for \(t>0\).

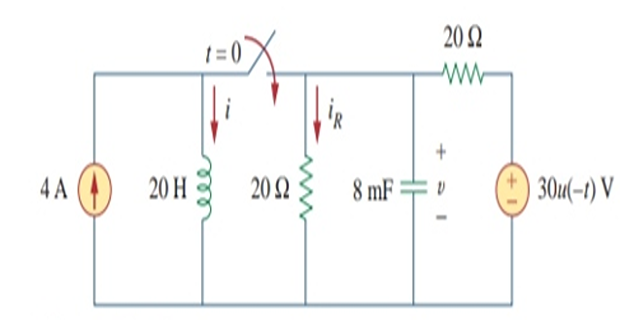
Solution-1

\[i(0)=4 \mathrm{~A}\]
, the switch is open, and the circuit is partitioned into two independent subcircuits. The 4-A current flows through the inductor, so that For
\[v(0)=\frac{20}{20+20}(30)=15 \mathrm{~V}\]
resistor connected in parallel with it. By voltage division, the initial capacitor voltage is . The capacitor acts like an open circuit and the voltage across it is the same as the voltage across the , the voltage source is operative for and 0 when when Since

For \(t>0 \Rightarrow\) switch closed \(\Rightarrow\) parallel \(R L C\) circuit with current source.
The voltage source is zero which means it acts like a short-circuit.
The two \(20-\Omega\) resistors are in parallel to give \(R=20 \| 20=10 \Omega\).
\[\begin{gathered} \alpha=\frac{1}{2 R C}=\frac{1}{2 \times 10 \times 8 \times 10^{-3}}=6.25 \\ \omega_{0}=\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{20 \times 8 \times 10^{-3}}}=2.5 \\ s_{1,2}=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}}=-6.25 \pm \sqrt{39.0625-6.25} \\ =-6.25 \pm 5.7282 \end{gathered}\]
The characteristic roots are determined as follows:
or \(s_{1}=-11.978, \quad s_{2}=-0.5218\)

\[i(t)=I_{s}+A_{1} e^{-11.978 t}+A_{2} e^{-0.5218 t} \cdots \cdots (1)\]
\(i(t)\)\(I_{s}=4\), we have the overdamped case. Hence, Since
We now use the initial conditions to determine \(A_{1}\) and \(A_{2}\).
\[i(0)=4=4+A_{1}+A_{2} \quad \Rightarrow \quad A_{2}=-A_{1} \cdots (2)\]
, At
\[\frac{d i}{d t}=-11.978 A_{1} e^{-11.978 t}-0.5218 A_{2} e^{-0.5218 t}\]
\[\frac{d i(0)}{d t}=-11.978 A_{1}-0.5218 A_{2} \cdots (3)\]
\(t=0\) in Eq. (1), Taking the derivative of

\[L \frac{d i(0)}{d t}=v(0)=15 \quad \Rightarrow \quad \frac{d i(0)}{d t}=\frac{15}{L}=\frac{15}{20}=0.75\]
But
\[0.75=(11.978-0.5218) A_{2} \Rightarrow A_{2}=0.0655\]
Substituting this into Eq. (3) and incorporating Eq. (2), we get
Thus, \(A_{1}=-0.0655\) and \(A_{2}=0.0655 .\)
\[i(t)=4+0.0655\left(e^{-0.5218 t}-e^{-11.978 t}\right) \mathrm{A}\]
in Eq. (1) gives the complete solution as and Inserting
\[i_{R}(t)=\frac{v(t)}{20}=\frac{L}{20} \frac{d i}{d t}=0.785 e^{-11.978 t}-0.0342 e^{-0.5218 t} \mathrm{~A}\]
and , we obtain From

Problem-2

Determine \(v(t)\) for \(t>0\)?

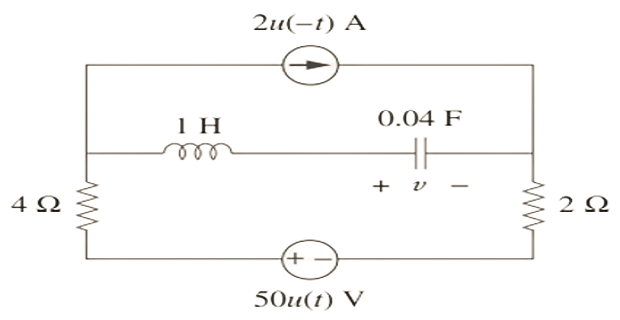
Solution-2

\[\begin{aligned} i(0^{-}) & = 0 \quad v(0^{-})&=-2\times 6 = -12~\mathrm{V} \end{aligned}\]

\[\begin{gathered} \alpha=\mathrm{R} /(2 \mathrm{~L})=6 / 2=3, \omega_{\mathrm{o}}=1 / \sqrt{\mathrm{LC}}=1 / \sqrt{0.04} \\ \mathrm{~s}=-3 \pm \sqrt{9-25}=-3 \pm \mathrm{j} 4 \end{gathered}\]

circuit with a step input. , we have a series For

\[\begin{gathered} \mathrm{v}(\mathrm{t})=50+\left[(A \cos 4 \mathrm{t}+B \sin 4 \mathrm{t}) \mathrm{e}^{-3 \mathrm{t}}\right] \\ \mathrm{v}(0)=-12=50+A \Rightarrow A=-62 \\ \mathrm{i}(0)=0=\operatorname{Cdv}(0) / \mathrm{dt} \end{gathered}\]

\[\begin{aligned} \mathrm{dv} / \mathrm{dt}=&\left[-3(\mathrm{~A} \cos 4 \mathrm{t}+\mathrm{B} \sin 4 \mathrm{t}) \mathrm{e}^{-3 \mathrm{t}}\right]+\left[4(-\mathrm{A} \sin 4 \mathrm{t}+\mathrm{B} \cos 4 \mathrm{t}) \mathrm{e}^{-3 \mathrm{t}}\right] \\ 0=& \mathrm{dv}(0) / \mathrm{dt}=-3 \mathrm{~A}+4 \mathrm{~B} \text { or } \mathrm{B}=(3 / 4) \mathrm{A}=-46.5 \\ & \mathrm{v}(\mathrm{t})=\left\{\mathbf{5 0}+\left[(-\mathbf{6 2} \cos 4 \mathrm{t}-\mathbf{4 6 . 5} \sin 4 \mathrm{t}) \mathrm{e}^{-3 \mathrm{t}}\right]\right\} \mathbf{V} \end{aligned}\]

final capacitor voltage where Thus,

Problem-3

Determine \(v(t)\) for \(t>0\)?

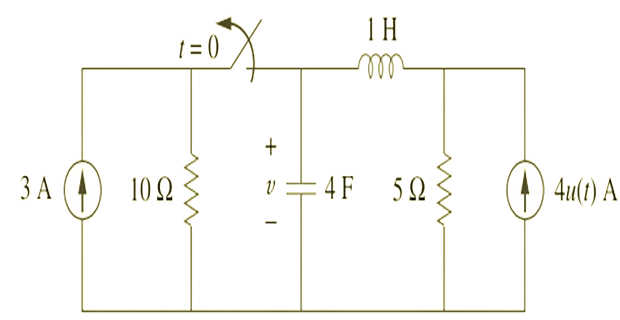
Solution-3

\[\begin{aligned} i(0)&=30/15 = 2~\mathrm{A}\\ v(0)&=5\times 30/15 = 10~\mathrm{V} \end{aligned}\]

\[\begin{aligned} t>0 & \Rightarrow \text{series RLC}\\ \alpha & = -R/(2L) = -2.5 \\ \omega_0 & = 1/\sqrt{LC}= 0.5\\ \alpha & > \omega_0 \Leftarrow \text{{\textcolor{magenta}{overdamped}}} \end{aligned}\]

Convert current to voltage source

\[\begin{aligned} &\mathrm{s}_{1,2}=-\alpha \pm \sqrt{\alpha^{2}-\omega_{\mathrm{o}}^{2}}=-2.5 \pm \sqrt{6.25-0.25}=-4.95,-0.0505 \\ &\mathrm{v}(\mathrm{t})=\mathrm{V}_{\mathrm{s}}+\left[\mathrm{A}_{1} \mathrm{e}^{-4.95 \mathrm{t}}+\mathrm{A}_{2} \mathrm{e}^{-0.0505 \mathrm{t}}\right], \quad \mathrm{V}_{\mathrm{s}}=20 \\ &\mathrm{v}(0)=10=20+\mathrm{A}_{1}+\mathrm{A}_{2} \Rightarrow \mathrm{A}_{2}=-10-\mathrm{A}_{1} \cdots (1) \\ &\mathrm{i}(0)=\mathrm{Cdv}(0) / \mathrm{dt} \text { or } \mathrm{dv}(0) / \mathrm{dt}=2 / 4=1 / 2 \\ & \quad 0.5=-4.95 \mathrm{~A}_{1}-0.0505 \mathrm{~A}_{2} \cdots (2) \\ &\text { From (1) and (2), }\\ &0.5=-4.95 \mathrm{~A}_{1}+0.505\left(10+\mathrm{A}_{1}\right) \text { or } \\ &-4.445 \mathrm{~A}_{1}=-0.005 \\ &\mathrm{~A}_{1}=0.001125, \mathrm{~A}_{2}=-10.001 \\ &\mathrm{v}(\mathrm{t})=\left[\underline{\mathbf{2 0}}+\mathbf{0 . 0 0 1 1 2 5} \mathrm{e}^{-4.95 \mathrm{t}}-\mathbf{1 0 . 0 0 1} \mathrm{e}^{-0.05 \mathrm{t}}\right] \mathbf{V} \end{aligned}\]

Problem-4

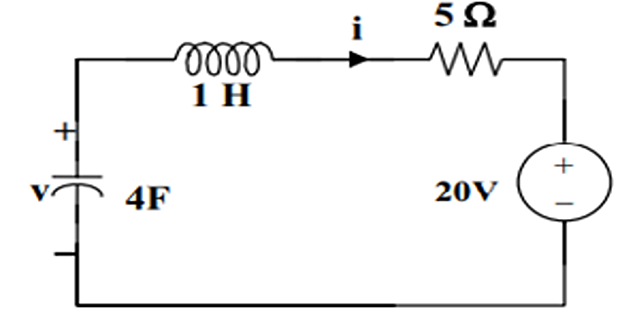
Determine \(i(t)\) for \(t>0\)?

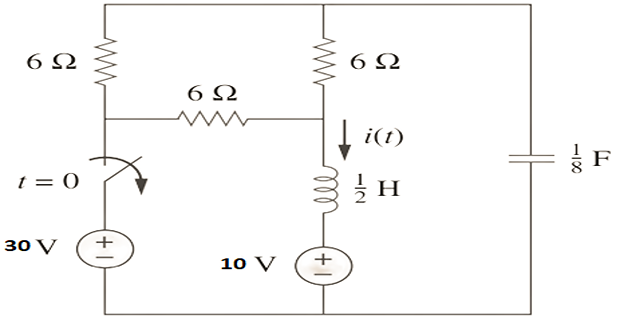
Solution-4

\[\begin{aligned} & \text{At}~t=0^{-} \\ &18 \mathrm{i}_{2}-6 \mathrm{i}_{1}=0 \text { or } \mathrm{i}_{1}=3 \mathrm{i}_{2}~\cdots (1) \\ &-30+6\left(\mathrm{i}_{1}-\mathrm{i}_{2}\right)+10=0 \text { or } \mathrm{i}_{1}-\mathrm{i}_{2}=10 / 3~ \cdots (2) \end{aligned}\]

From (1) and (2).

\[\begin{gathered} \mathrm{R}=6 \| 12=4 \\ \omega_{\mathrm{o}}=1 / \sqrt{\mathrm{LC}}=1 / \sqrt{(1 / 2)(1 / 8)}=4 \\ \alpha=\mathrm{R} /(2 \mathrm{~L})=(4) /(2 \mathrm{x}(1 / 2))=4 \\ \alpha=\omega_{\mathrm{o}}, \text { therefore the {\textcolor{magenta}{circuit is critically damped }}}\\ \mathrm{v}(\mathrm{t})=\mathrm{V}_{\mathrm{s}}+\left[(\mathrm{A}+\mathrm{Bt}) \mathrm{e}^{-4 \mathrm{t}}\right], \text { and } \mathrm{V}_{\mathrm{s}}=10 \\ \mathrm{v}(0)=20=10+\mathrm{A}, \text { or } \mathrm{A}=10 \\ \mathrm{i}_{\mathrm{C}}=\mathrm{Cdv} / \mathrm{dt}=\mathrm{C}\left[-4(10+\mathrm{Bt}) \mathrm{e}^{-4 \mathrm{t}}\right]+\mathrm{C}\left[(\mathrm{B}) \mathrm{e}^{-4 \mathrm{t}}\right] \end{gathered}\]

circuit. , we have a series For

\[\begin{aligned} \mathrm{i}_{\mathrm{C}}=\mathrm{Cdv} / \mathrm{dt}=&(1 / 8)\left[-4(10+0 \mathrm{t}) \mathrm{e}^{-4 \mathrm{t}}\right]+(1 / 8)\left[(0) \mathrm{e}^{-4 \mathrm{t}}\right] \\ & \mathrm{i}_{\mathrm{C}}(\mathrm{t})=\left[-(1 / 2)(10) \mathrm{e}^{-4 \mathrm{t}}\right] \\ & \mathrm{i}(\mathrm{t})=-\mathrm{i}_{\mathrm{C}}(\mathrm{t}) = \mathbf{5} \mathrm{e}^{-4 \mathrm{t}} \mathbf{A} \end{aligned}\]

\(\mathrm{B}=0\)\(-40=-40+\mathrm{B}\)\(\mathrm{i}_{\mathrm{C}}(0)=-5=\mathrm{C}(-40+\mathrm{B})\)

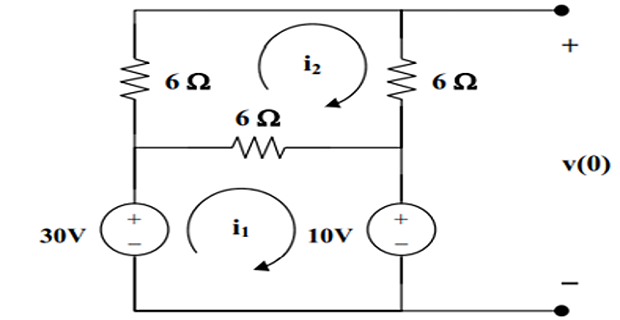
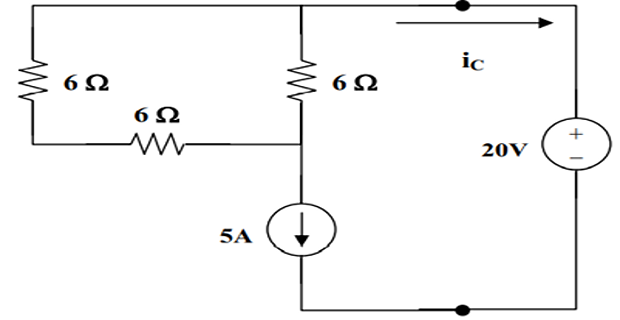
Problem-5

The switch is moved from \(a\) to \(b\) at \(t=0\). Determine \(i(t)\) for \(t>0\)?

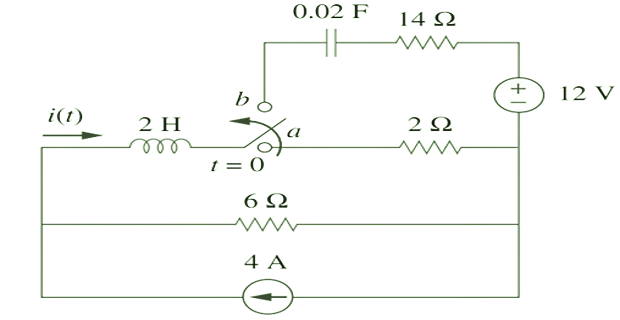
Solution-5

\[\begin{aligned} \omega_{\mathrm{o}}&=1 / \sqrt{\mathrm{LC}}=1 / \sqrt{2 \times 0.02}=5\\ \alpha&=\mathrm{R} /(2 \mathrm{~L})=(6+14) /(2 \times 2)=5 \end{aligned}\]

and At

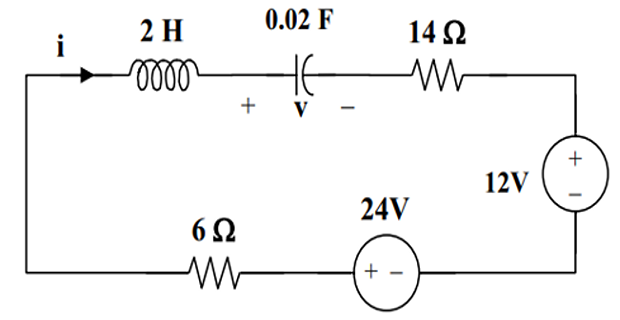
Since \(\alpha=\omega_{\mathrm{o}}\), critically damped response

\[\begin{gathered} \mathrm{v}(\mathrm{t})=\mathrm{V}_{\mathrm{s}}+\left[(\mathrm{A}+\mathrm{Bt}) \mathrm{e}^{-5 \mathrm{t}}\right], \quad \mathrm{V}_{\mathrm{s}}=24-12=12 \mathrm{~V} \\ \mathrm{v}(0)=0=12+\mathrm{A} \text { or } \mathrm{A}=-12 \\ \mathrm{i}=\mathrm{Cdv} / \mathrm{dt}=\mathrm{C}\left\{\left[\mathrm{Be}^{-5 \mathrm{t}}\right]+\left[-5(\mathrm{~A}+\mathrm{B} \mathrm{t}) \mathrm{e}^{-5 \mathrm{t}}\right]\right\} \\ \mathrm{i}(0)=3=\mathrm{C}[-5 \mathrm{~A}+\mathrm{B}]=0.02[60+\mathrm{B}] \text { or } \mathrm{B}=90 \\ \text { Thus, } \mathrm{i}(\mathrm{t})=0.02\left\{\left[90 \mathrm{e}^{-5 \mathrm{t}}\right]+\left[-5(-12+90 \mathrm{t}) \mathrm{e}^{-5 \mathrm{t}}\right]\right\} \\ \left.\mathrm{i}(\mathrm{t})=\{\mathbf{3}-9 \mathrm{t}) \mathrm{e}^{-5 \mathrm{t}}\right\} \mathbf{A} \end{gathered}\]

Problem-6

Determine \(i(t)\) and \(v(t)\) for \(t>0\)?

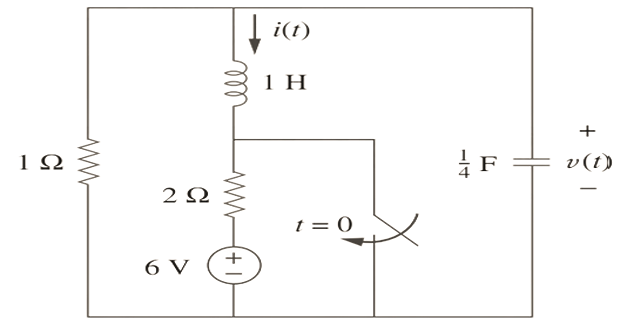
Solution-6

For \(t=0^{-} \Rightarrow i(0)=-6 /(1+2)=-2\) and \(v(0)=2 \times 1=2\)

\[\begin{gathered} \alpha=1 /(2 \mathrm{RC})=(1) /(2 \times 1 \times 0.25)=2 \\ \omega_{0}=1 / \sqrt{\mathrm{LC}}=1 / \sqrt{1 \times 0.25}=2 \end{gathered}\]
, the voltage is SC For
\[\mathrm{s}_{1,2}=-2\]
, Since

\[\begin{aligned} \mathrm{i}(\mathrm{t})=&\left[(\mathrm{A}+\mathrm{Bt}) \mathrm{e}^{-2 \mathrm{t}}\right], \quad \mathrm{i}(0)=-2=\mathrm{A} \\ \mathrm{v}=& \text { Ldi} / \mathrm{dt}=\left[\mathrm{Be}^{-2 \mathrm{t}}\right]+\left[-2(-2+\mathrm{B} \mathrm{t}) \mathrm{e}^{-2 \mathrm{t}}\right] \\ & \mathrm{v}_{\mathrm{o}}(0)=2=\mathrm{B}+4 \text { or } \mathrm{B}=-2 \\ & \text { Thus, } \mathrm{i}(\mathrm{t})=\left[(-2-2 \mathrm{t}) \mathrm{e}^{-2 \mathrm{t}}\right] \mathbf{A} \\ \text { and } \mathrm{v}(\mathrm{t})=&\left[(2+4 \mathrm{t}) \mathrm{e}^{-2 \mathrm{t}}\right] \mathbf{V} \end{aligned}\]

Thus,

Problem-7

Determine \(i(t)\) for \(t>0\)?

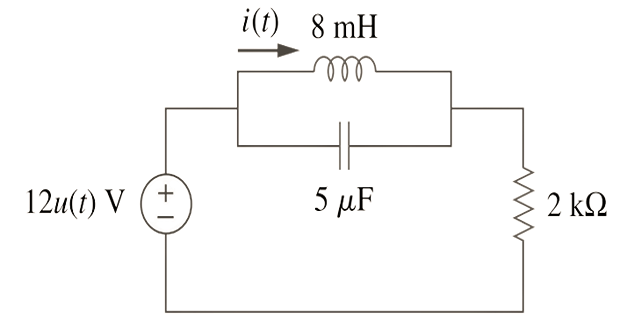
Solution-7

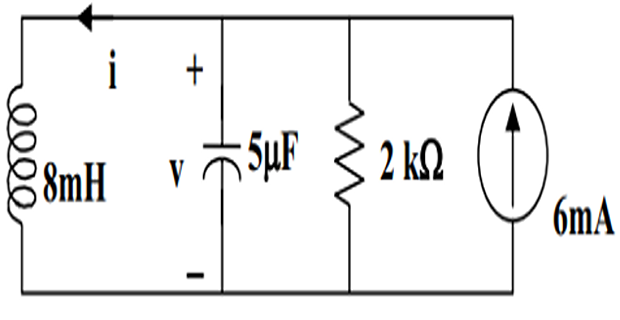
For \(t=0^{-}, u(t)=0\), so that \(v(0)=0\) and \(i(0)=0\).
\[\begin{aligned} &\alpha=1 /(2 R C)=(1) /\left(2 \times 2 \times 10^{3} \times 5 \times 10^{-6}\right)=50 \\ &\omega_{0}=1 / \sqrt{L C}=1 / \sqrt{8 \times 10^{-3} \times 5 \times 10^{-6}}=5,000 \end{aligned}\]
, For
\[\mathrm{s}_{1,2}=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}} \cong-50 \pm \mathrm{j} 5,000\]
, Since

\[\begin{aligned} \mathrm{i}(\mathrm{t}) &=\mathrm{I}_{\mathrm{s}}+\left[(\mathrm{A} \cos 5,000 \mathrm{t}+\mathrm{B} \sin 5,000 \mathrm{t}) \mathrm{e}^{-50 \mathrm{t}}\right], \quad \mathrm{I}_{\mathrm{s}}=6 \mathrm{~mA} \\ \mathrm{i}(0) &=0=6+\mathrm{A} \\ & \text { or } \mathrm{A}=-6 \mathrm{~m} \mathrm{~A} \\ \mathrm{v}(0) &=0=\mathrm{Ldi}(0) / \mathrm{dt} \\ \mathrm{di} / \mathrm{dt} &=\left[5,000(-\mathrm{A} \sin 5,000 \mathrm{t}+\mathrm{B} \cos 5,000 \mathrm{t}) \mathrm{e}^{-50 \mathrm{t}}\right]+\\ &\left[-50(\mathrm{~A} \cos 5,000 \mathrm{t}+\mathrm{B} \sin 5,000 \mathrm{t}) \mathrm{e}^{-50 \mathrm{t}}\right] \\ \mathrm{di}(0) / \mathrm{dt} &=0=5,000 \mathrm{~B}-50 \mathrm{~A} \\ & \text { or } \mathrm{B}=0.01(-6)=-0.06 \mathrm{~mA} \\ \mathrm{i}(\mathrm{t}) &=\mathbf{6}-[\mathbf{6} \cos \mathbf{5}, \mathbf{0 0 0 t}+\mathbf{0 . 0 6 s i n 5}, \mathbf{0 0 0 t}) \mathrm{e}^{-50 \mathrm{t}} \mathbf{m A} \end{aligned}\]

Problem-8

Determine \(i(t)\) for \(t>0\)?

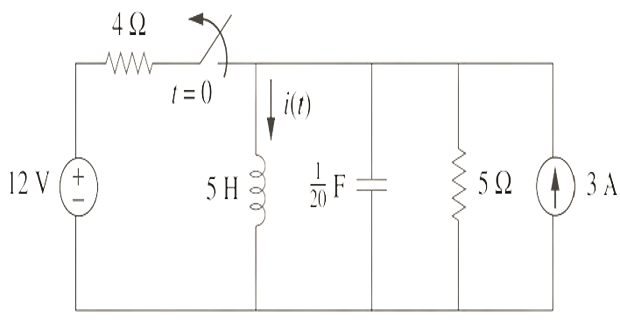
Solution-8

For \(\mathrm{t}=0^{-}, \mathrm{i}(0)=3+12 / 4=6\) and \(\mathrm{v}(0)=0\)
\[\begin{gathered} \alpha=1 /(2 R C)=(1) /(2 \times 5 \times 0.05)=2 \\ \omega_{o}=1 / \sqrt{L C}=1 / \sqrt{5 \times 0.05}=2 \end{gathered}\]
, For
\[\begin{gathered} \mathrm{s}_{1,2}=-2 \\ \mathrm{i}(\mathrm{t})=\mathrm{I}_{\mathrm{s}}+\left[(\mathrm{A}+\mathrm{Bt}) \mathrm{e}^{-2 \mathrm{t}}\right], \quad \mathrm{I}_{\mathrm{s}}=3 \\ \mathrm{i}(0)=6=3+\mathrm{A} \text { or } \mathrm{A}=3 \\ \mathrm{v}=\mathrm{Ldi} / \mathrm{dt} \text { or } \mathrm{v} / \mathrm{L}=\mathrm{di} / \mathrm{dt}=\left[\mathrm{Be}^{-2 \mathrm{t}}\right]+\left[-2(\mathrm{~A}+\mathrm{Bt}) \mathrm{e}^{-2 \mathrm{t}}\right] \\ \mathrm{v}(0) / \mathrm{L}=0=\mathrm{di}(0) / \mathrm{dt}=\mathrm{B}-2 \times 3 \text { or } \mathrm{B}=6\\ \mathrm{i}(\mathrm{t})=\left\{3+\left[(3+6 \mathrm{t}) \mathrm{e}^{-2 \mathrm{t}}\right]\right\} \mathrm{A} \end{gathered}\]
, Since

Problem-9

Determine \(i(t)\) for \(t>0\)?

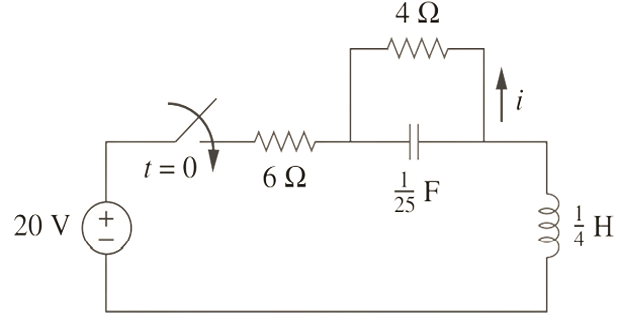
Solution-9

\[\begin{aligned} t<0 & \Rightarrow i(0)=0,\quad v(0)=0 \end{aligned}\]

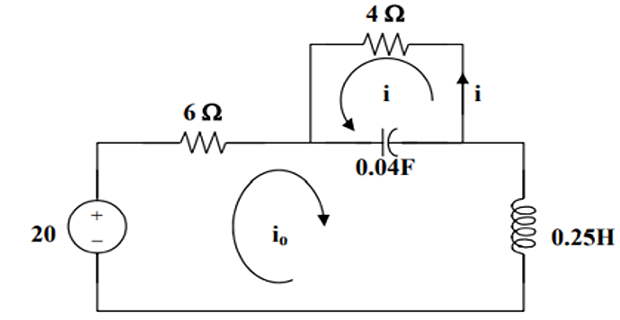
KVL in larger loop, \(-20+6 \mathrm{i}_{0}+0.25 \mathrm{di}_{0} / \mathrm{dt}+25 \int\left(\mathrm{i}_{0}+\mathrm{i}\right) \mathrm{dt}=0 \cdots (1)\)
smaller loop, \(\quad 4 \mathrm{i}+25 \int\left(\mathrm{i}+\mathrm{i}_{\mathrm{o}}\right) \mathrm{dt}=0\) or \(\int\left(\mathrm{i}+\mathrm{i}_{\mathrm{o}}\right) \mathrm{dt}=-0.16 \mathrm{i} \cdots (2)\)
Taking derivative, \(\quad 4 \mathrm{di} / \mathrm{dt}+25\left(\mathrm{i}+\mathrm{i}_{0}\right)=0 \Rightarrow \mathrm{i}_{0}=-0.16 \mathrm{di} / \mathrm{dt}-\mathrm{i} \cdots (3)\)
And \(\mathrm{di}_{0} / \mathrm{dt}=0.16 \mathrm{~d}^{2} \mathrm{i} / \mathrm{dt}^{2}-\mathrm{di} / \mathrm{dt} \cdots (4)\)
From (1), (2), (3), and (4), \(\quad-20-0.96 \mathrm{di} / \mathrm{dt}-6 \mathrm{i}-0.04 \mathrm{~d}^{2} \mathrm{i} / \mathrm{dt}^{2}-0.25 \mathrm{di} / \mathrm{dt}-4 \mathrm{i}=0\)
Which becomes, \(\quad \mathrm{d}^{2} \mathrm{i} / \mathrm{dt}^{2}+30.25 \mathrm{di} / \mathrm{dt}+250 \mathrm{i}=-500\)

This leads to, \(s^{2}+30.25 s+250=0\) or \(s_{1,2}=\frac{-30.25 \pm \sqrt{(30.25)^{2}-1000}}{2}=-15.125 \pm \mathrm{j} 4.608\) underdamped
Thus, \(\mathrm{i}(\mathrm{t})=\mathrm{I}_{\mathrm{s}}+\mathrm{e}^{-15.125 \mathrm{t}}\left(\mathrm{A}_{1} \cos (4.608 \mathrm{t})+\mathrm{A}_{2} \sin (4.608 \mathrm{t})\right) \mathrm{A}\)
At \(\mathrm{t}=0, \mathrm{i}_{\mathrm{o}}(0)=0\) and \(\mathrm{i}(0)=0=\mathrm{I}_{\mathrm{s}}+\mathrm{A}_{1}\) or \(\mathrm{A}_{1}=-\mathrm{I}_{\mathrm{s}}\).
As \(\mathrm{t} \rightarrow \infty\), \(\mathrm{i}_{\mathrm{o}}(\infty)=\) \(20 / 10=2 \mathrm{~A}=-\mathrm{i}(\infty)\) or \(\mathrm{i}(\infty)=-2 \mathrm{~A}=\mathrm{I}_{\mathrm{s}}\) and \(\mathrm{A}_{1}=2\).
From (3), \(\operatorname{di}(0) / \mathrm{dt}=-6.25 \mathrm{i}_{\mathrm{o}}(0)-6.25 \mathrm{i}(0)=0\). \(\mathrm{di} / \mathrm{dt}=0-15.125 \mathrm{e}^{-15.125 \mathrm{t}}\left(\mathrm{A}_{1} \cos (4.608 \mathrm{t})+\mathrm{A}_{2} \sin (4.608 \mathrm{t})\right)+\mathrm{e}^{-15.125 \mathrm{t}}\left(-\mathrm{A}_{1} 4.608 \sin (4.608 \mathrm{t})\right.\) \(\left.+\mathrm{A}_{2} 4.608 \cos (4.608 \mathrm{t})\right)\) .
\[\begin{aligned} \operatorname{di}(0) / \mathrm{dt}&=0=-15.125 \mathrm{~A}_{1}+4.608 \mathrm{~A}_{2}=-30.25+4.608 \mathrm{~A}_{2}\\ \text{or} & \mathrm{A}_{2}=30.25 / 4.608=6.565 \end{aligned}\]
, At
\[\mathrm{i}(\mathrm{t})=\underline{\left(-2+\mathrm{e}^{-15.125 \mathrm{t}}(2 \cos (4.608 \mathrm{t})+6.565 \sin (4.608 \mathrm{t})) A\right.}\]
This leads to,

Problem-10

The switch has been closed for a long time and then opened at \(t=0\). Determine \(i_x\) and \(v_R\) for \(t>0\).

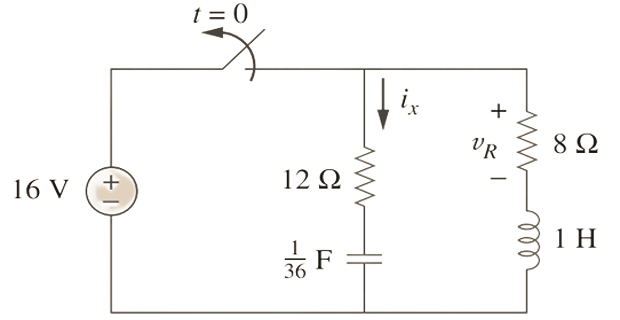
Solution-10

Let \(\mathrm{v}=\) capacitor voltage and \(\mathrm{i}=\) inductor current.
\[\mathrm{v}(0-)=16 \mathrm{~V} \text { and } \mathrm{i}(0-)=16 / 8=2 \mathrm{~A}\]
switch is closed and circuit has reached steady-state. At
At \(\mathrm{t}=0+\), the switch is open but, \(\mathrm{v}(0+)=16\) and \(\mathrm{i}(0+)=2\).
\[\begin{gathered} \mathrm{R} = 8+12=20 \Omega, \mathrm{L}=1 \mathrm{H}, \mathrm{C}=4 \mathrm{mF} . \\ \alpha=\mathrm{R} /(2 \mathrm{~L})=(20) /(2 \mathrm{x} 1)=10 \\ \omega_{\mathrm{o}}=1 / \sqrt{\mathrm{LC}}=1 / \sqrt{1 \times(1 / 36)}=6 \end{gathered}\]
We now have a
\[\mathrm{s}_{1,2}=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}}=-18,-2\]
, Since
Characteristic equation is \((\mathrm{s}+2)(\mathrm{s}+18)=0\) or \(\underline{\mathbf{s}^{2}+\mathbf{2 0 s}+\mathbf{3 6}=\mathbf{0}}\).

\(\mathrm{i}(\mathrm{t})=\left[\mathrm{Ae}^{-2 \mathrm{t}}+\mathrm{Be}^{-18 \mathrm{t}}\right]\) and \(\mathrm{i}(0)=2=\mathrm{A}+\mathrm{B} \cdots (1)\)
To get \(\operatorname{di}(0) / \mathrm{dt}\), consider the circuit below at \(\mathrm{t}=0+\).

\[\begin{aligned} & -v(0)+20 i(0)+v_{L}(0)=0 \\ & -16+20 \times 2+v_{\mathrm{L}}(0)=0 \\ & v_{\mathrm{L}}(0)=-24\\ & \operatorname{Ldi}(0) / \mathrm{dt}=\mathrm{v}_{\mathrm{L}}(0) \\ & \operatorname{di}(0) / \mathrm{dt}=\mathrm{v}_{\mathrm{L}}(0) / \mathrm{L}=-24 \mathrm{~A} / \mathrm{s}\\ &-24=-2 \mathrm{~A}-18 \mathrm{~B}\\ & 12=\mathrm{A}+9 \mathrm{~B} \cdots (2) \end{aligned}\]

\[\begin{aligned} \mathrm{i}(\mathrm{t})&=\left[0.75 \mathrm{e}^{-2 \mathrm{t}}+1.25 \mathrm{e}^{-18 \mathrm{t}}\right]=-\mathrm{i}_{\mathrm{x}}(\mathrm{t}) \\ \mathrm{i}_{\mathrm{x}}(\mathrm{t})&=(-\mathbf{0 . 7 5} \mathrm{e}^{-2 \mathrm{t}}-\mathbf{1 . 2 5} \mathrm{e}^{-18 \mathrm{t}})~ \mathrm{A} \\ \mathrm{v}(\mathrm{t})&=8 \mathrm{i}(\mathrm{t})=\underline{\mathbf{6}^{-2 \mathrm{t}}+\mathbf{1 0} \mathrm{e}^{-18 \mathrm{t}}} \underline{\mathbf{A}} \end{aligned}\]

and From (1) and (2),