Demonstrative Video
Problem-1
Using Mesh analysis find \(V_0\) ?
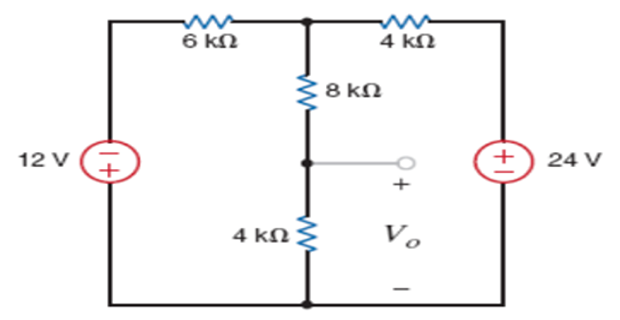
Solution-1
- \[\begin{aligned} &12=4\left(I_{1}-I_{2}\right)+8\left(I_{1}-I_{2}\right)+6 I_{1} \\ &\Rightarrow 12=18 I_{1}-12 I_{2} \\ &\Rightarrow 2=3 I_{1}-2 I_{2} \end{aligned}\]\(\underline{K V L}\)
KVL in the second loop:
\[\begin{aligned} 24 &=4 I_{2}+8\left(I_{2}-I_{1}\right)+4\left(I_{2}-I_{1}\right) \\ \Rightarrow 24 &=16 I_{2}-12 I_{1} \\ 6 &=4 I_{2}-3 I_{1} \end{aligned}\]- \[\begin{aligned} &I_{1}=10 / 3 \mathrm{~mA}, I_{2}=4 \mathrm{~mA} \\ &V_{0}=4 \times\left(I_{2}-I_{1}\right) \\ &\Rightarrow V_{0}=4 \times\left(4-\frac{10}{3}\right) \mathrm{Volts} ~ \Rightarrow V_{0}=8 / 3=2.667 \mathrm{Volts} \end{aligned}\]From equation (1) and (2)
Problem-2
Apply mesh analysis to the circuit to obtain \(I_0\).
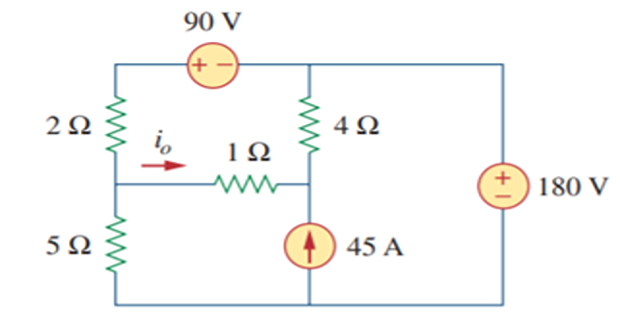
Solution-2
- \[6 \mathrm{i}_{1}+4 \mathrm{i}_{2}-5 \mathrm{i}_{3}+180=0\]Loop 1 and 2 form a supermesh. For the supermesh,
For loop 3, \(-\mathrm{i}_{1}-4 \mathrm{i}_{2}+7 \mathrm{i}_{3}+90=0\)
Also, \(\mathrm{i}_{2}=45+\mathrm{i}_{1}\)
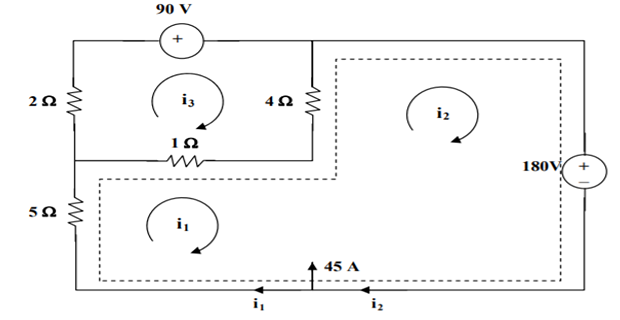
Solving \(, i_{1}=-46, i_{3}=-20 ; \quad \mathrm{i}_{0}=\mathrm{i}_{1}-\mathrm{i}_{3}=-\mathbf{2 6} \mathbf{A}\)
Problem-3
The power delivered by the current source ?
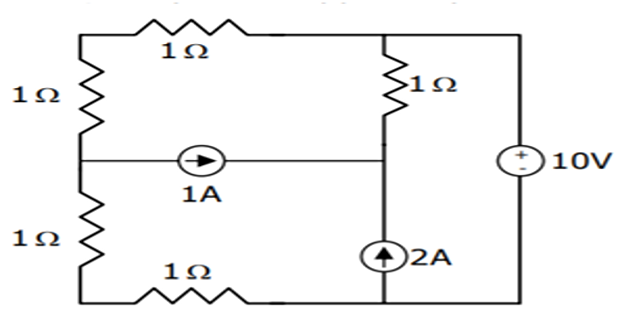
Solution-3
- \[\begin{aligned} (3+i) 2+(2+i) 2 &=10 \\ \Rightarrow \quad 6+2 i+4+2 i &=10 \\ \Rightarrow \quad 4 i &=0 \\ \Rightarrow \quad i &=0 \end{aligned}\]Applying KVL in outer loop,
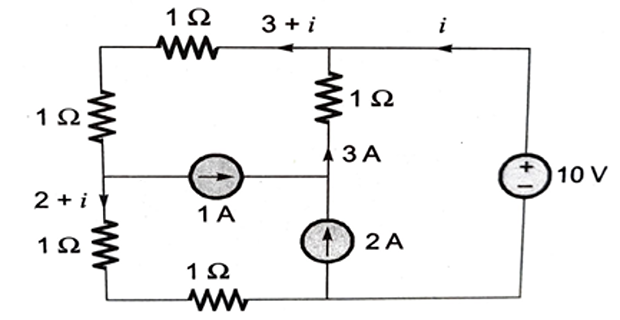
- \[\begin{aligned} P &=V i \\ &=10 \times 0=0~ W \end{aligned}\]Power supplied by the voltage source,
Problem-4
Find \(i_x\) and \(v_x\) ?
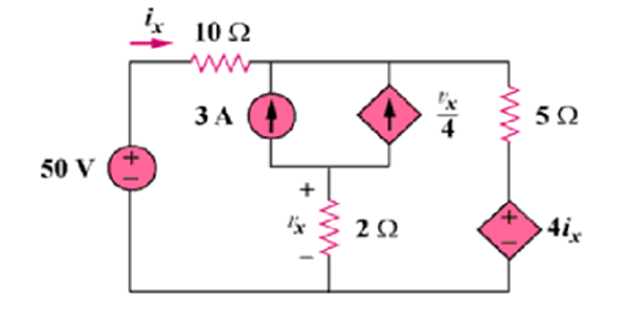
Solution-4
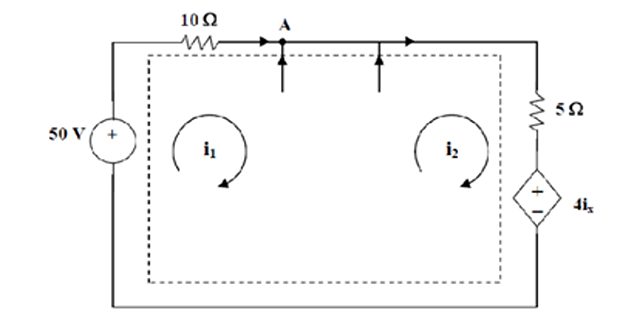
For the supermesh, \(-50+10 \mathrm{i}_{1}+5 \mathrm{i}_{2}+4 \mathrm{i}_{\mathrm{x}}=0\),
but \(\mathrm{i}_{\mathrm{x}}=\mathrm{i}_{1} .\)
Hence, \(50-14 \mathrm{i}_{1}+5 \mathrm{i}_{2}\)
At node \(A, i_{1}+3+\left(v_{x} / 1\right)=i_{2}\),
but \(v_{x}=2\left(i_{1}-i_{2}\right)\),
hence, \(i_{1}+2=i_{2}\)
- \[\begin{aligned} \mathrm{i}_{1}&=2.10 .5 \mathrm{~A}\\ \mathrm{i}_{2}&=4.105 \mathrm{~A}\\ v_{x}&=2\left(i_{1}-i_{2}\right)=4~\mathrm{Volts}\\ i_{x}&=i_{2}-2=\underline{2.105} \mathrm{amp} \end{aligned}\]Solving (1) and (2) gives
Problem-5
Use mesh analysis in determining the power absorbed by the dependent voltage source ?
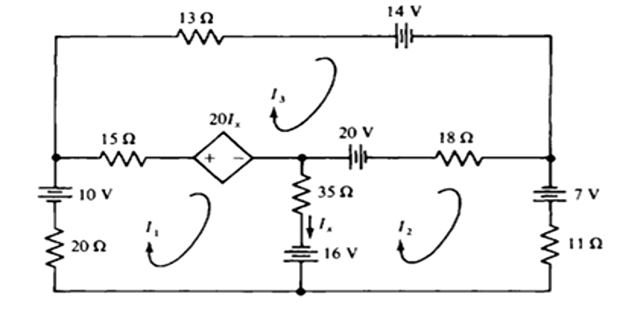
Solution-5
- \[\begin{aligned} 70 I_{1}-35 I_{2}-15 l_{3}+20\left(I_{1}-I_{2}\right) &=10+16 \\ -35 I_{1}+64 I_{2}-18 I_{3} &=7-16-20 \\ -15 I_{1}-18 I_{2}+46 l_{3}-20\left(I_{1}-l_{2}\right) &=20-14 \end{aligned}\]The mesh equations are as:
- \[\left[\begin{array}{rrr} 90 & -55 & -15 \\ -35 & 64 & -18 \\ -35 & 2 & 46 \end{array}\right]\left[\begin{array}{l} I_{1} \\ l_{2} \\ I_{3} \end{array}\right]=\left[\begin{array}{r} 26 \\ -29 \\ 6 \end{array}\right]\]which simplify to
The solutions are \(I_{1}=0.148\) A. \(I_{2}=-0.3 \mathrm{~A}\), and \(I_{3}=0.256 \mathrm{~A}\).
- \[P=20\left(I_{1}-I_{2}\right)\left( I_{1}-I_{3}\right)=20(0.148+0.3)(0.148-0.256)=-0.968 \mathrm{~W}\]Finally, the power absorbed by the dependent source is equal to the source voltage times the current flow into the positive-referenced terminal:
Problem-6
Find currents \(I_1\), \(I_2\), and \(I_3\) ?
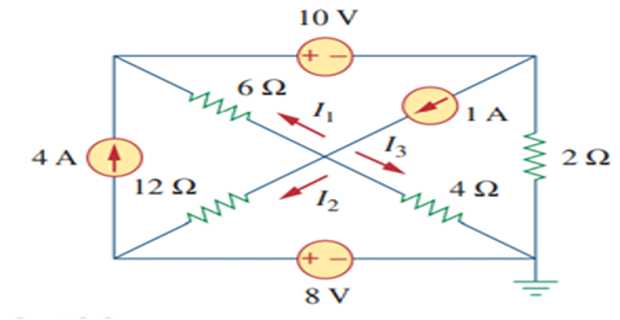
Solution-6
It is evident that \(\quad I_{1}=4\)
- \[12\left(\mathrm{I}_{4}-\mathrm{I}_{1}\right)+4\left(\mathrm{I}_{4}-\mathrm{I}_{3}\right)-8=0\]For mesh 4,
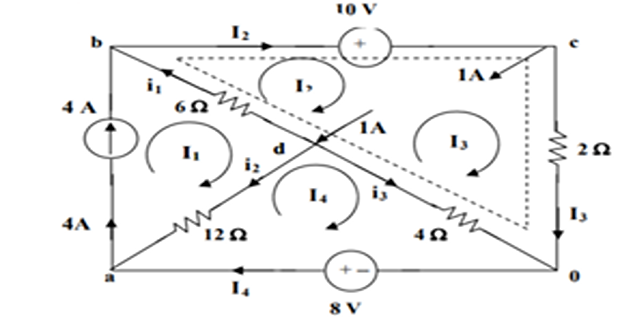
- \[6\left(\mathrm{I}_{2}-\mathrm{I}_{1}\right)+10+2 \mathrm{I}_{3}+4\left(\mathrm{I}_{3}-\mathrm{I}_{4}\right)=0 \Rightarrow -3 \mathrm{I}_{1}+3 \mathrm{I}_{2}+3 \mathrm{I}_{3}-2 \mathrm{I}_{4}=-5\]For the super mesh
At node \(\mathbf{c}, \quad \mathbf{I}_{2}=\mathbf{I}_{3}+1\)
Solving yields, \(I_{1}=4 \mathrm{~A}, \mathrm{I}_{2}=3 \mathrm{~A}, \mathrm{I}_{3}=2 \mathrm{~A}\), and \(\mathrm{I}_{4}=4 \mathrm{~A}\)
At node \(\mathbf{b}, \quad \mathrm{i}_{1}=\mathrm{I}_{2}-\mathrm{I}_{1}=\mathbf{- 1} \mathbf{A}\)
At node a, \(\quad \mathrm{i}_{2}=4-\mathrm{I}_{4}=\mathbf{0} \mathrm{A}\)
At node \(0, \quad \mathrm{i}_{3}=\mathrm{I}_{4}-\mathrm{I}_{3}=\mathbf{2} \mathbf{A}\)
Problem-7
Find the values of mesh currents ?
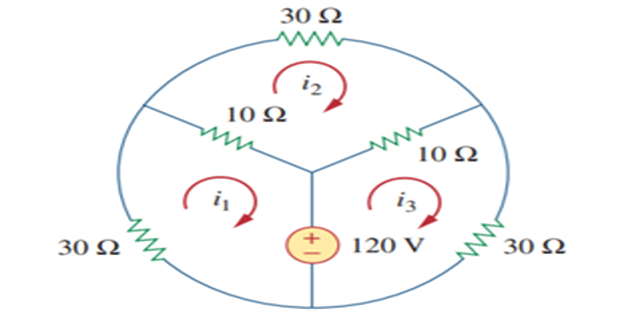
Solution-7
For loop-1 \(120+40 \mathrm{i}_{1}-10 \mathrm{i}_{2}=0 \Rightarrow -12=4 \mathrm{i}_{1}-\mathrm{i}_{2}\)
For loop-2 \(50 \mathrm{i}_{2}-10 \mathrm{i}_{1}-10 \mathrm{i}_{3}=0 \Rightarrow -\mathrm{i}_{1}+5 \mathrm{i}_{2}-\mathrm{i}_{3}=0\)
For loop-3 \(-120-10 \mathrm{i}_{2}+40 \mathrm{i}_{3}=0 \Rightarrow12=-\mathrm{i}_{2}+4 \mathrm{i}_{3}\)
Solving \(i_{1}=-3 \mathbf{A}, i_{2}=\mathbf{0}\), and \(i_{3}=\mathbf{3 A}\)
Problem-8
Find \(v_0\) using mesh analysis ?
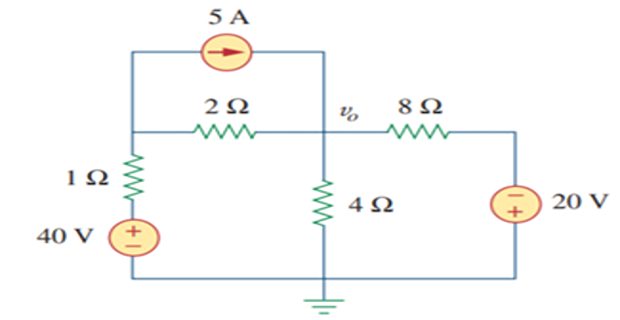
Solution-8
For loop-1 , \(i_{1}=5 \mathrm{~A}\)
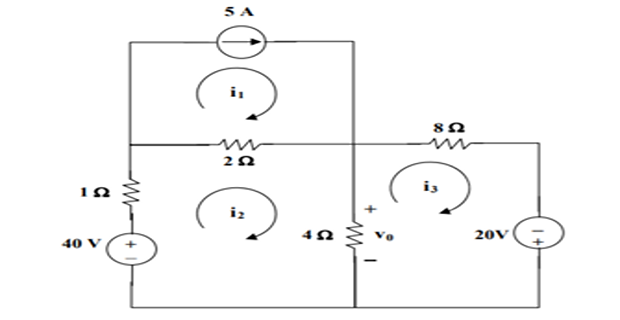
For loop-2 \(-40+7 \mathrm{i}_{2}-2 \mathrm{i}_{1}-4 \mathrm{i}_{3}=0 \Rightarrow50=7 \mathrm{i}_{2}-4 \mathrm{i}_{3}\)
For loop-3, \(-20+12 \mathrm{i}_{3}-4 \mathrm{i}_{2}=0 \Rightarrow 5=-\mathrm{i}_{2}+3 \mathrm{i}_{3}\)
Solving with \((2)\) and (3), \(\quad i_{2}=10 \mathrm{~A}, \mathrm{i}_{3}=5 \mathrm{~A}\)
And, \(\mathrm{v}_{0}=4\left(\mathrm{i}_{2}-\mathrm{i}_{3}\right)=4(10-5)=\mathbf{2 0} \mathbf{V}\).