Demonstrative Video
Problem-1
Determine the maximum power delivered to the resistor \(R\).

Solution-1

\[\begin{aligned}
V_0 & = \dfrac{2 K\Omega}{5 K\Omega}(5) =
2~\mathrm{V} \\
V_{oc} & = V_{TH} = V_{40 K\Omega} =
\dfrac{40K\Omega}{50K\Omega}(200)=160~\mathrm{V}\\
I_{sc} & = \dfrac{200}{10K\Omega} = 20~\mathrm{mA}
\\
R_{th} & = \dfrac{V_{th}}{I_{sc}} =
\dfrac{160\mathrm{V}}{20\mathrm{mA}}=8~K\Omega \\
P_{max} & = \dfrac{V_{th}^2}{4R_L} =
\dfrac{160^2}{4\times 8K\Omega} = 0.8~\mathrm{W}
\end{aligned}\]
Problem-2
Determine the value of \(R_L\) for maximum power transfer.
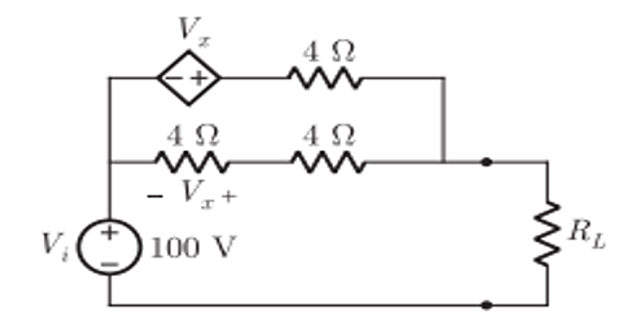
Solution-2

\[\begin{aligned}
V_1 & = V_x +4\left(I_1-\dfrac{V_x}{4}\right)=4I_1\\
R_{th} & = \dfrac{V_1}{I_1} = 4~\Omega
\end{aligned}\]
Problem-3
Find the value of R in the circuit such that maximum power transfer takes place. What is the amount of this power?

Solution-3

\[\begin{aligned}
\text{Mesh-1}~3i_1-2i_2 & = 4\\
\text{Mesh-2}~8i_2-2i_1 & = 0\\
\text{solving}~i_2 & = \dfrac{2}{5}~\mathrm{A} \\
\because 1\times i_2 + 6 & = V_{oc} \\
\Rightarrow V_{oc} & = \left(6+\dfrac{2}{5}\right)\\
& =\dfrac{32}{5}~\mathrm{V}
\end{aligned}\]