First-Order Circuits Made Simple: Conquer Exams with Solved Problems!

Demonstrative Video

Concepts of First-Order Circuits

Problem-1

Determine the Time-constant of the network?

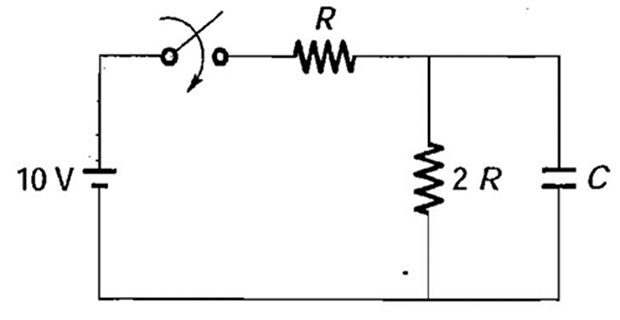
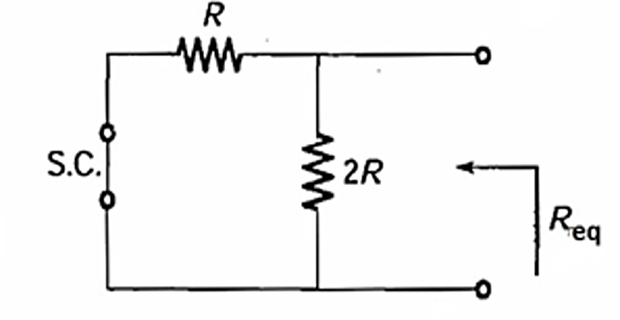
Solution-1

\[\begin{aligned} R_{Th} & = R || (2R) = \dfrac{2}{3} R \\ \tau & = R_{Th} \cdot C = \dfrac{2}{3} RC~ \mathrm{sec.} \end{aligned}\]

Problem-2

In the circuit shown, the initial capacitor voltage is 4 V. Switch \(S_1\) is closed at \(t=0\). Find the charge lost by the capacitor from \(t=25~\mu s\) to \(t=100~\mu s\) ?

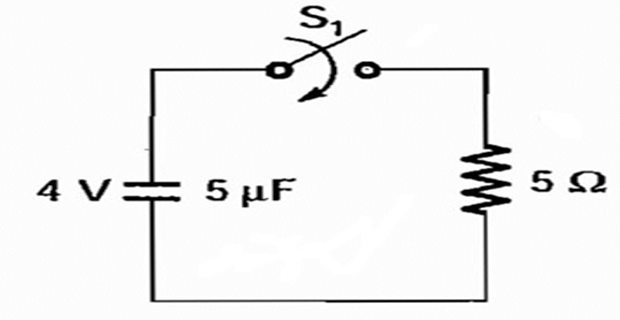
Solution-2

\[\begin{aligned} \tau & = R\cdot C = 25\times 10^{-6}~\text{sec} \\ i(t) & = \dfrac{V}{R} e^{-t/\tau} = \dfrac{4}{5} e^{-t/\tau} \end{aligned}\]
Current
\[\begin{aligned} Q & = \int_{25~\mu s}^{100~\mu s} i(t) dt = 6.99\times 10^{-6}~\mathrm{C} \end{aligned}\]
Charge lost by the capacitor:

Problem-3

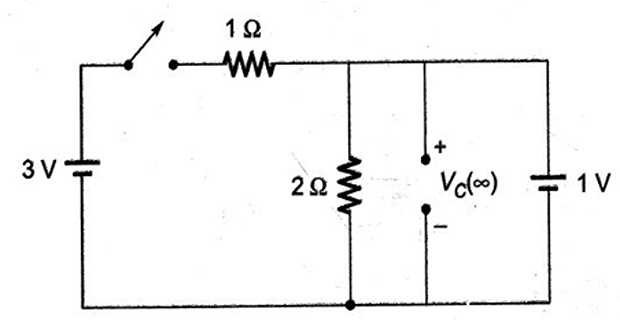
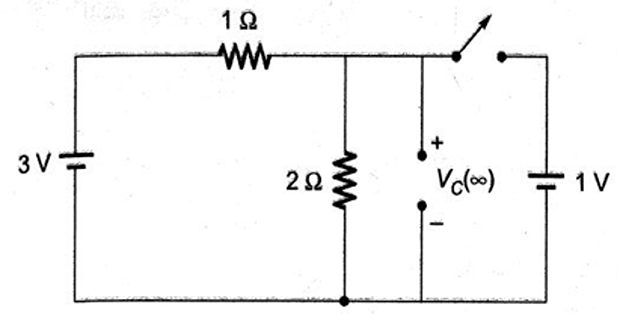
\(S_1\) was closed and \(S_2\) was open for a very long time. At \(t=0\), \(S_1\) is opened and \(S_2\) is closed. Determine the voltage across the capacitor at \(t=5~\mu s\) ?

Solution-3

\[\begin{aligned} \text{At}~t&=\infty\\ V_c(\infty)&=3\dfrac{2}{2+1}=2~\mathrm{V} \end{aligned}\]

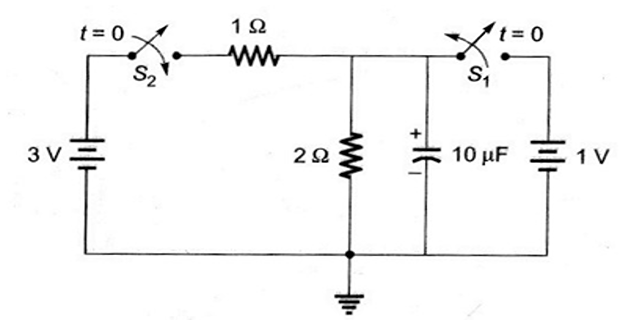
\[\begin{aligned} & \tau = RC = \dfrac{2}{3}\times 10 \times 10^{-6}\\ & V_c(t) =[V_c(0^{+})-V_c(\infty)]e^{-t/\tau}+V_c(\infty)\\ &=[1-2]e^{-t/\tau}+2 \end{aligned}\]

Step-3

Problem-4

The switch in the figure below has been closed for a long time ,and it opens at \(t=0\) .Find \(V(t)\) for \(t \geq 0\)

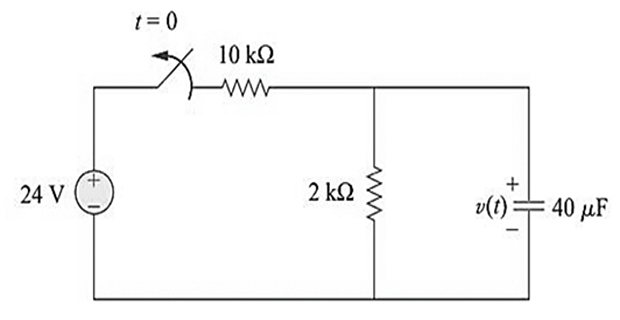
Solution-4

\[\begin{aligned} &\mathrm{v}_{\mathrm{o}}=\mathrm{v}(0)=\frac{2}{10+2}(24)=4 \mathrm{~V} \\ &\mathrm{v}(\mathrm{t})=\mathrm{v}_{\mathrm{o}} \mathrm{e}^{-\mathrm{t} / \tau}\\ &\tau=\mathrm{RC}=40 \times 10^{-6} \times 2 \times 10^{3}=\frac{2}{25} \\ &\mathrm{v}(\mathrm{t})=4 \mathrm{e}^{-12.5 \mathrm{t}} \mathrm{V} \end{aligned}\]

Problem-5

For the circuit in figure below, find \(v_0(t)\) for \(t > 0\) . Determine the time necessary for the capacitor voltage to decay to one-third of its value at \(t = 0\).

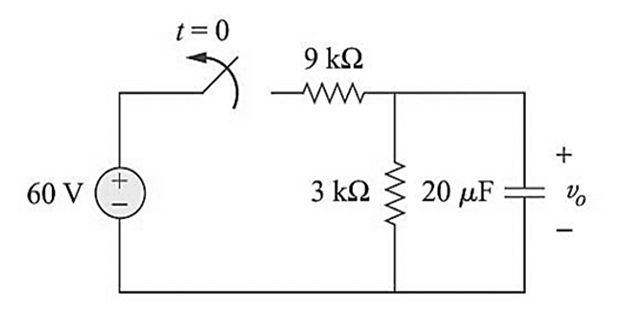
Solution-5

For \(\mathrm{t}<0\), \(v\left(0^{-}\right)=\frac{3}{3+9}(36 V)=9 V\)
\[\begin{aligned} \tau=R C&=3 \times 10^{3} \times 20 \times 10^{-6} =0.06 s \\ v_{0}(t) &=9 \mathbf{e}^{-16.667 t} \mathbf{V} \end{aligned}\]
circuit , we have a source-free For
\[\begin{aligned} 3&=9 \mathrm{e}^{-16.667t_0}\\ \mathrm{e}^{16.667 t_0}&=9 / 3=3\\ t_0&=\ln (3) / 16.667=\mathbf{6 5 . 9 2} \mathbf{~ m s} \end{aligned}\]
. Let the time be

Problem-6

Determine the current \(i(t)\) through the capacitor?

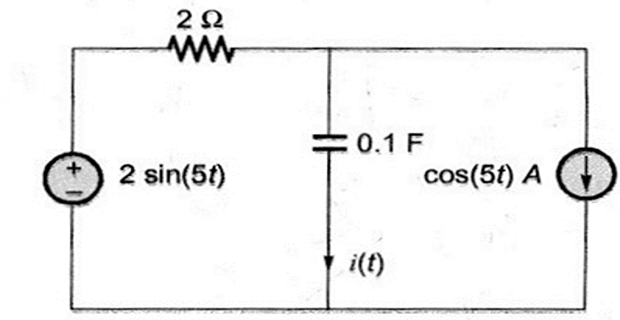
Solution-6

Applying Source Transformation

\[\begin{aligned} Z &=\sqrt{R^{2}+\frac{1}{(C \omega)^{2}}}\\ &=\sqrt{4+\frac{1}{(0.1 \times 5)^{2}}} =2 \sqrt{2} \\ i &=\frac{2 \sqrt{2} \sin \left(5 t-45^{\circ}\right)}{2 \sqrt{2} \angle(-45)}=\sin 5 t \mathrm{~A} \end{aligned}\]

Problem-7

The capacitor shown in the figure is initially charged to 10 V. The switch closes at time \(t=0\) . Find the value of \(V_c(t)\) in volts at time \(t=10\) ms ?

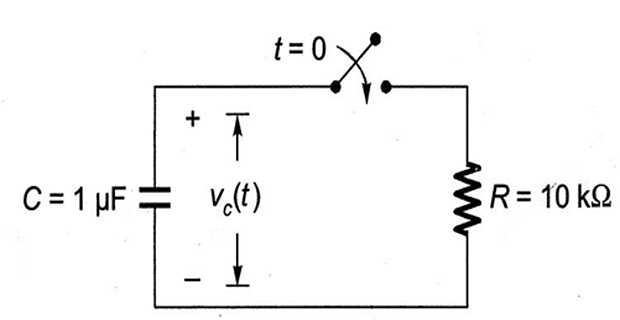
Solution-7

\[\begin{aligned} v_{c}(t) &=V_{o} e^{-t / \tau} \\ &=10 e^{-100 t}\left[\because \tau=R C=\frac{1}{100}\right] \\ \therefore v_{c}(\text { at } 10 ~& \text{msec})=10 e^{\left(-100 \times 10 \times 10^{-3}\right)} \\ &=3.678 \mathrm{~V} \end{aligned}\]

Problem-8

In Figure, the capacitor initially has a charge of 10 coloumb. The current in the circuit 1 second after the switch ‘S’ is closed will be

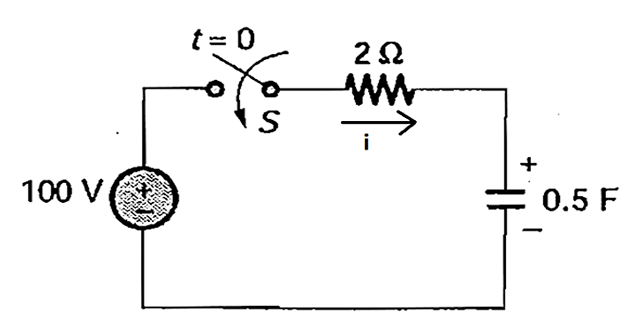
Solution-8

\[\begin{aligned} V_{c}\left(0^{-}\right) &=V_{c}\left(0^{+}\right)=\frac{Q}{C} = \frac{10}{0.5}=20 \mathrm{~V} \\ V_{c}(\infty)=& 100 \mathrm{~V} \\ \end{aligned}\]

switch is closed At

\[\begin{aligned} V_{c}(t)=& V_{c}(\infty)+\left\{V_{c}\left(0^{+}\right)-V_{c}(\infty)\right\} e^{-t/ R C} \\ V_{c}(t)=& 100+(20-100) e^{--t/ 1} \\ \therefore \quad i_{c}(t)=& C \frac{d V_{c}(t)}{d t} \\ =& 0.5 \times-80 \times\left(-e^{-t}\right)=40 e^{-t} \\ \left.i_{c}(t)\right|_{t=1}=& 40 e^{-1} = 14.71 \mathrm{~A} \end{aligned}\]

Problem-9

The initial charge in the 1F capacitor present in the circuit shown is zero. Find the energy in joules transformed from the DC source until steady state condition is reached?

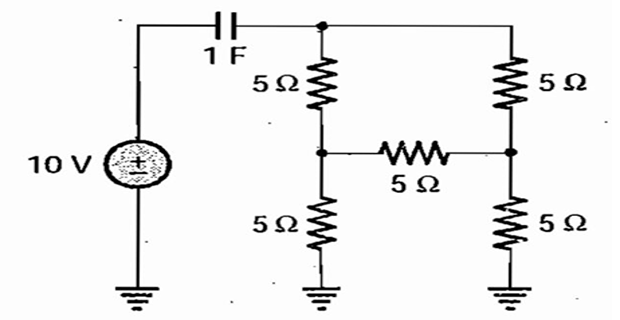
Solution-9

DELTA \(\rightarrow\) STAR

\[i(t)=\frac{V}{R} e^{-t / \tau}=\frac{10}{3} e^{-t / 5}=2 e^{-0.2 t}\]

\[E=\int_{0}^{\infty} 10 \times 2 e^{-0.2 t} d t=100 \mathrm{~J}\]

. Now current, Here,

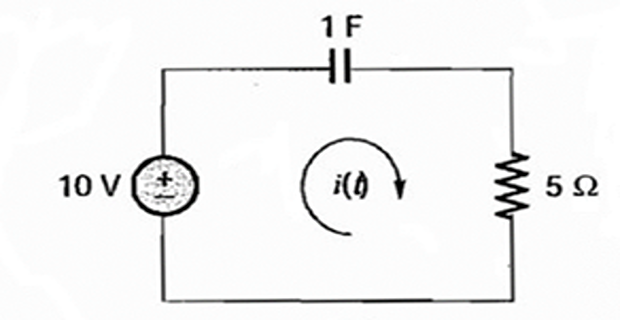
Problem-10

Find the energy absorbed by the 4 \(\Omega\) in time interval \(( 0, \infty)\) ? . Given \(V_c(0) = 6\) V

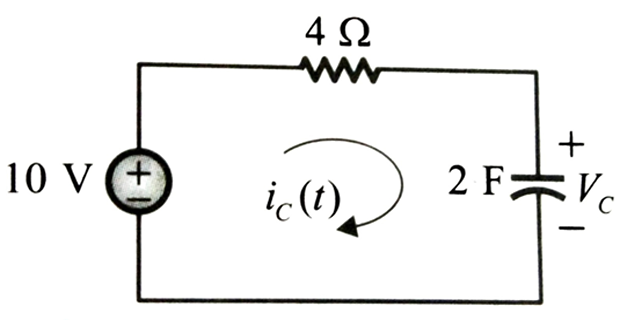
Solution-10

\[\begin{aligned} &i_{C}(t)=i_{C}(\infty)+\left[i_{C}\left(0^{+}\right)-i_{C}(\infty)\right] e^{-t / \tau}\\ &V_{C}\left(0^{-}\right)=V_{C}\left(0^{+}\right)=6 \mathrm{~V} \quad \text { [Given] } \end{aligned}\]

We know:

\[\tau = RC = 8~\text{sec}\]

At \(t>0\)Transient

\[\begin{aligned} i_{C}(t) &=e^{-t / 8} \mathrm{~A} \end{aligned}\]

Substituting we get,

\[\begin{aligned} P &=i_{C}^{2}(t) R \\ E &=\int_{0}^{\infty} P d t=\int_{0}^{\infty} i_{C}^{2}(t) R d t=\int_{0}^{\infty}\left(e^{-t / 8}\right)^{2} \times 4 d t \\ E &=\int_{0}^{\infty} 4 e^{-t / 4} d t=4 \times(-4)\left[e^{-t / 4}\right]_{t=0}^{\infty} \\ E &=-16[0-1]=16 \text { Joules } \end{aligned}\]

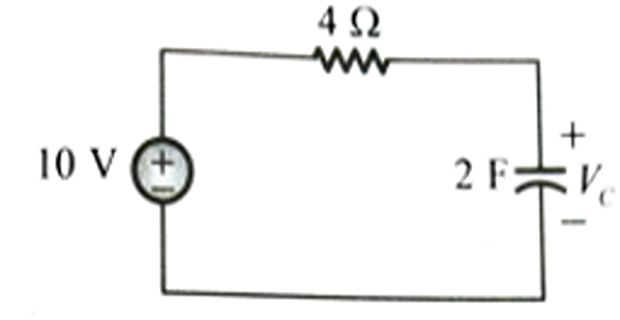
RL Circuits

Problem-11

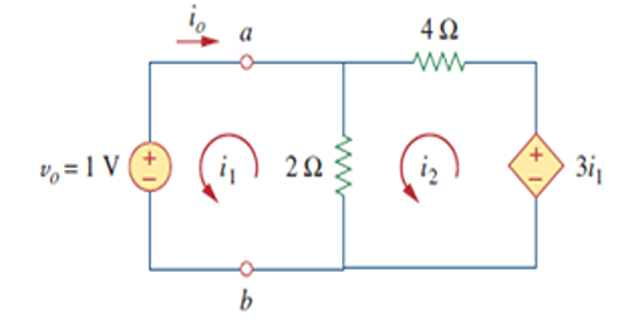
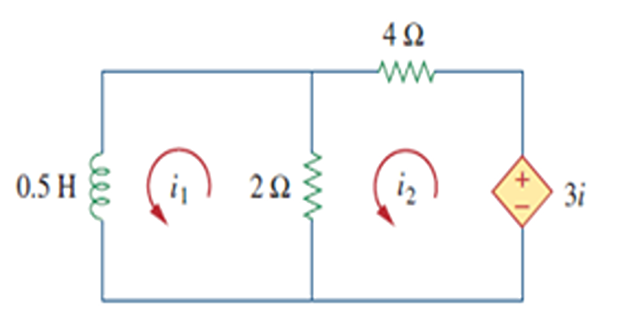
Assuming that \(i(0)\)=10 A, Calculate \(i(t)\) and \(i_x(t)\)

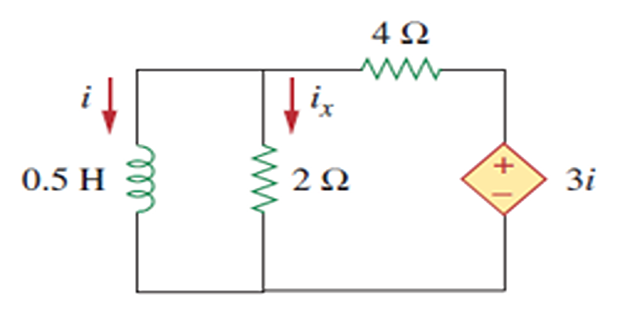
Solution-11

\[\begin{aligned} &2\left(i_{1}-i_{2}\right)+1=0 \\ &6 i_{2}-2 i_{1}-3 i_{1}=0 \\ &i_{1}=-3 \mathrm{~A}, \quad i_{o}=-i_{1}=3 \mathrm{~A} \\ &R_{\mathrm{eq}}=R_{\mathrm{Th}}=\frac{v_{o}}{i_{o}}=\frac{1}{3} \Omega \\ &\tau=\frac{L}{R_{\mathrm{eq}}}=\frac{\frac{1}{2}}{\frac{1}{3}}=\frac{3}{2} \mathrm{~s} \\ &i(t)=i(0) e^{-t / \tau}\\ &=10 e^{-(2 / 3) t} \mathrm{~A}, \quad t>0 \end{aligned}\]

Method-1:

\[\begin{aligned} &\frac{1}{2} \frac{d i_{1}}{d t}+2\left(i_{1}-i_{2}\right)=0 \Rightarrow \frac{d i_{1}}{d t}+4 i_{1}-4 i_{2}=0 \\ &6 i_{2}-2 i_{1}-3 i_{1}=0 \quad \Rightarrow \quad i_{2}-\frac{5}{6} i_{1} \\ &\frac{d i_{1}}{d t}+\frac{2}{3} i_{1}=0 \quad \Rightarrow \quad \frac{d i_{1}}{i_{1}}=-\frac{2}{3} d t \\ &\left.\ln i\right|_{i(0)} ^{i(0)}=-\left.\frac{2}{3} t\right|_{0} ^{t} \quad \Rightarrow \ln \frac{i(t)}{i(0)}=-\frac{2}{3} t \\ &i(t)=i(0) e^{-(2 / 3) t}=10 e^{-(2 / 3) t} \mathrm{~A}, \quad t>0 \end{aligned}\]

Method-2:

\[\begin{aligned} &v=L \frac{d i}{d t}=0.5(10)\left(-\frac{2}{3}\right) e^{-(2 / 3) t}=-\frac{10}{3} e^{-(2 / 3) t} \mathrm{~V} \\ &i_{x}(t)=\frac{v}{2}=-1.6667 e^{-(2 / 3) t} \mathrm{~A}, \quad t>0 \end{aligned}\]

Problem-12

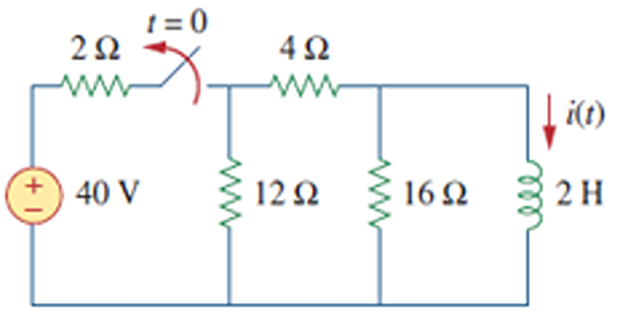
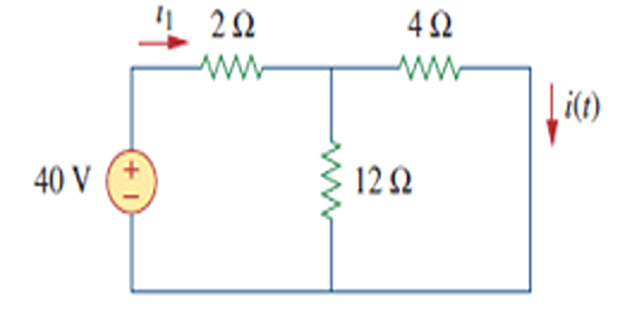
The switch has been closed for a long time. At \(t=0\), the switch is opened. Calculate \(i(t)\) for \(t>0\).

Solution-12

\(t<0~\Rightarrow~S~\text{closed}~\Rightarrow ~L\) short \(\Rightarrow~16\Omega\) short

\[\begin{aligned} R_{eq} & = \dfrac{4\times 12}{4+12} = 3~\Omega \\ i_1 & = \dfrac{40}{2+3} = 8~\mathrm{A} \\ i(t) & = \dfrac{12}{12+4}i_1 = 6~\mathrm{A}, \quad t<0 \\ \end{aligned}\]

\[\begin{aligned} i(0^+) & = i(0^{-}) = 6~\mathrm{A} \\ R_{eq} & = (12+4)||16 = 8~\Omega \\ \tau & = \dfrac{L}{R_{eq}} =\dfrac{1}{4}~\mathrm{s}\\ i(t) & = i(0)e^{-t/\tau}= 6e^{-4t}~\mathrm{A} \end{aligned}\]

Problem-13

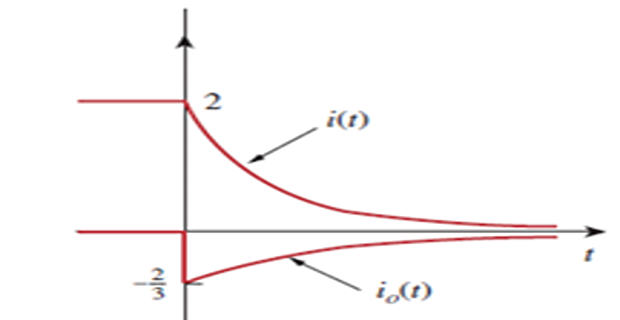
Find \(i_0\), \(v_0\), and \(i\) for all time , assuming that the switch was open for a long time.

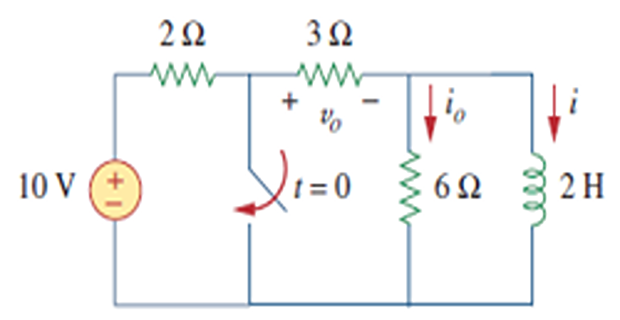
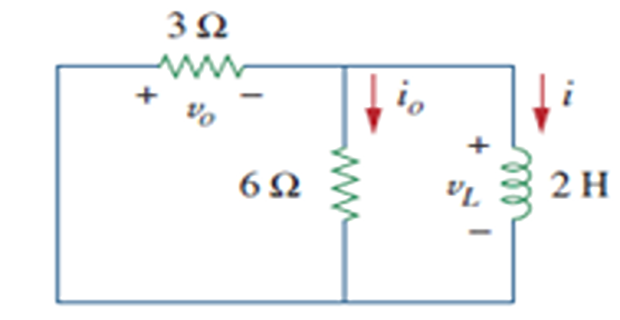
Solution-13

\(t<0~\Rightarrow~S~\text{open}~\Rightarrow ~L\) short \(\Rightarrow~6\Omega\) short

\[\begin{aligned} i_0&=0 \\ i(t) & = \dfrac{10}{2+3} = 2~\mathrm{A}, \quad t<0 \\ v_0(t)&=3i(t)=6~\mathrm{V},\quad t<0\\ i(0) & = 2 \end{aligned}\]

\[\begin{aligned} R_{Th} & = 3||6=2~\Omega \\ \tau & = \dfrac{L}{R_{Th}}=1~\mathrm{s} \\ i(t) & = i(0)e^{-t/\tau}=2e^{-t}~\mathrm{A}, \quad t>0\\ v_0(t)&=-v_L=-L\dfrac{di}{dt} =4e^{-t}~\mathrm{V},\quad t>0 \end{aligned}\]

\[i_{o}(t)=\frac{v_{L}}{6}=-\frac{2}{3} e^{-t} \mathrm{~A}, \quad t>0\]

Thus, for all time,

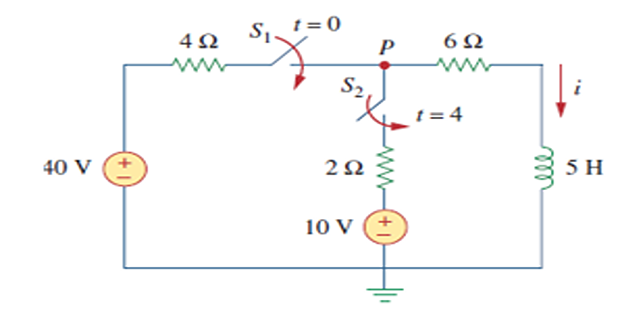
Problem-14

At \(t=0\), switch-1 is closed, and switch-2 is closed 4 s later. Find \(i(t)\) for \(t>0\). Calculate \(i\) for \(t=2\) s and \(t=5\) s.

Solution-14

Intervals \(t \leq 0,0 \leq t \leq 4\), and \(t \geq 4\) separately.
For \(t<0\), \(S_{1}\) and \(S_{2}~\Rightarrow\) open \(\Rightarrow i=0\).
\(i\left(0^{-}\right)=i(0)=i\left(0^{+}\right)=0\)

For \(0 \leq t \leq 4, ~S_{1}\) closed \(\Rightarrow 4-\Omega\) and \(6-\Omega\) are in series. (Remember, at this time, \(S_{2}\) is still open.)
\[\begin{gathered} i(\infty)=\frac{40}{4+6}=4 \mathrm{~A}, \quad R_{\mathrm{Th}}=4+6=10 \Omega \\ \tau=\frac{L}{R_{\mathrm{Th}}}=\frac{5}{10}=\frac{1}{2} \mathrm{~s} \end{gathered}\]
is closed forever, Hence, assuming for now that
\[\begin{aligned} i(t) &=i(\infty)+[i(0)-i(\infty)] e^{-t / \tau} \\ &=4+(0-4) e^{-2 t}=4\left(1-e^{-2 t}\right) \mathrm{A}, \quad 0 \leq t \leq 4 \end{aligned}\]
Thus,

For \(t \geq 4, ~S_{2}\) closed \(\Rightarrow\)10 - V connected.
\[i(4)=i\left(4^{-}\right)=4\left(1-e^{-8}\right) \simeq 4 \mathrm{~A}\]
This sudden change does not affect the inductor current because the current cannot change abruptly. Thus, the initial current is

\[\begin{gathered} \frac{40-v}{4}+\frac{10-v}{2}=\frac{v}{6} \quad \Rightarrow \quad v=\frac{180}{11} \mathrm{~V} \\ i(\infty)=\frac{v}{6}=\frac{30}{11}=2.727 \mathrm{~A} \end{gathered}\]
. Using KCL, be the voltage at node , let To find
\[R_{\mathrm{Th}}=4 \| 2+6=\frac{4 \times 2}{6}+6=\frac{22}{3} \Omega\]
\[\tau=\frac{L}{R_{\mathrm{Th}}}=\frac{5}{\frac{22}{3}}=\frac{15}{22} \mathrm{~s}\]
The Thevenin resistance at the inductor terminals is

\[i(t)=i(\infty)+[i(4)-i(\infty)] e^{-(t-4) / \tau}, \quad t \geq 4\]
Hence,
\[\begin{array}{rlr} i(t) & =2.727+(4-2.727) e^{-(t-4) / \tau}, & \tau=\frac{15}{22} \\ & =2.727+1.273 e^{-1.4667(t-4)}, & t \geq 4 \end{array}\]
in the exponential because of the time delay. Thus, We need
\[i(t)= \begin{cases}0, & t \leq 0 \\ 4\left(1-e^{-2 t}\right), & 0 \leq t \leq 4 \\ 2.727+1.273 e^{-1.4667(t-4)}, & t \geq 4\end{cases}\]
\[i(5)=2.727+1.273 e^{-1.4667}=3.02 \mathrm{~A}\]
\(t=5\)
\[i(2)=4\left(1-e^{-4}\right)=3.93 \mathrm{~A}\]
\(t=2\)Putting all this together,