Fundamentals of Electric Circuits and Networks

Problem-1

• Figure shows the current flowing through a capacitor. Determine the charge acquired by the capacitor up to first 5\(\mu\)sec.

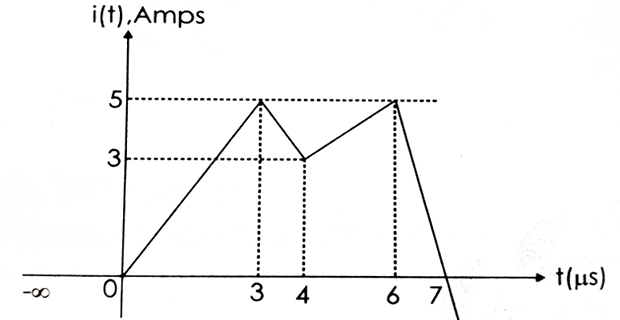
Solution-1

• We know current \(I=Q/t\) and Charge \(Q=I*t\)

• Charge acquired by capacitor= Area under I vs t graph for first 5\(\mu\)sec

Problem-2

• Two coils connected in parallel across 100-V dc supply, take 10 A current from the supply. Power dissipated in one coil is 600 W. What is the resistance of each coil?

Solution-2

• \[\mathrm{R}_{\mathrm{eff}}=100 / 10=10 \Omega\]
  The effective resistance of the two coils in parallel is
• \[\begin{aligned} &600=100^{2} / \mathrm{R}_{1} \\ &\Rightarrow \mathrm{R}_{1}=10000 / 600=16.67 \Omega \end{aligned}\]
  Power in one coil is given as
• \[\begin{aligned} &10=\frac{16.67 \times \mathrm{R}_{2}}{16.67+\mathrm{R}_{2}} \\ &\Rightarrow \mathbf{R}_{2}=\mathbf{2 5} \Omega \end{aligned}\]
  Since the two coils are connected in parallel, we should have

Problem-3

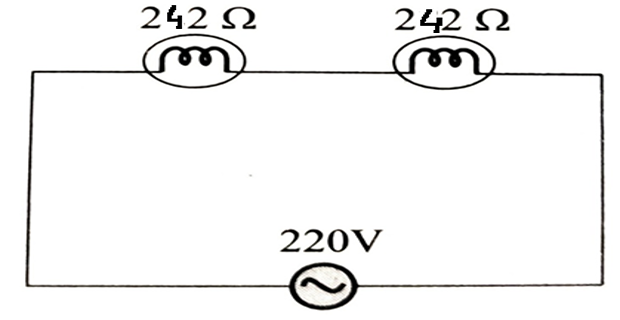
• How many 200W/220V incandescent lamps connected in series would consume the same total power as a single 100W/220V incandescent lamp?

Solution-3

• \[\begin{aligned} &\mathrm{R}_{1}=\frac{\mathrm{V}^{2}}{\mathrm{P}_{1}} \\ &=220^{2} / 200=242 \Omega \end{aligned}\]
  Resistance

• To make \(100 \mathrm{~W}\),

  \[\mathrm{R}_{2}=220^{2} / 100=484 \Omega\]

\[\mathrm{P}=220^{2} / 484=100 \mathrm{~W}\]

as By connecting 2 (lamps) in series we can get the

Problem-4

• When a resistor R is connected to a current source, it consumes a power of 18 W. When the same R is connected to a voltage source having the same magnitude as the current source, the power absorbed by R is 4.5 W. The magnitude of the current source and the value of R are?

Solution-4

• \[P_{1}=I^{2} R=18 \mathrm{~W}\]
  , With current source, I connected across
• \[\begin{aligned} \mathrm{P}_{2}=\mathrm{I}^{2} / \mathrm{R} \\ &=4.5 \mathrm{~W} \end{aligned}\]
  . With the voltage source of I volts connected across to the same
• \[\begin{aligned} \mathrm{P}_{1} \mathrm{P}_{2}=\mathrm{I}^{4}=& 18 \times 4.5 \\ =& 81 \\ \Rightarrow \mathrm{I}=& 3 \mathrm{~A} \\ \mathrm{R}=18 / 9=& 2 \Omega \end{aligned}\]
  Multiplying both equations

Problem-5

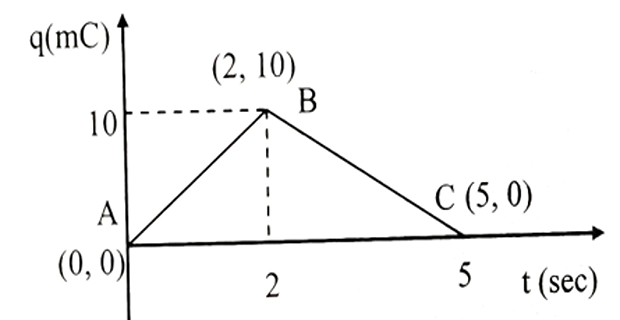
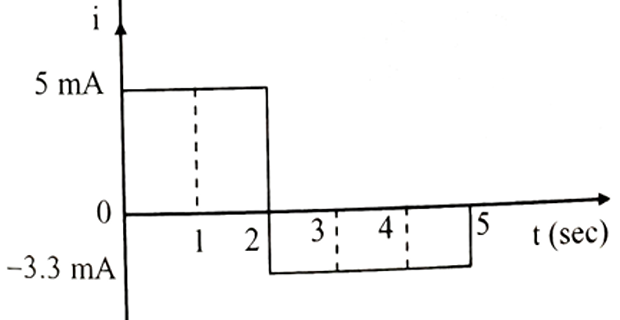
• The charge delivered by a constant voltage source is shown. Determine the current supplied by the source at

  1. t = 1 sec

  2. t = 3 sec

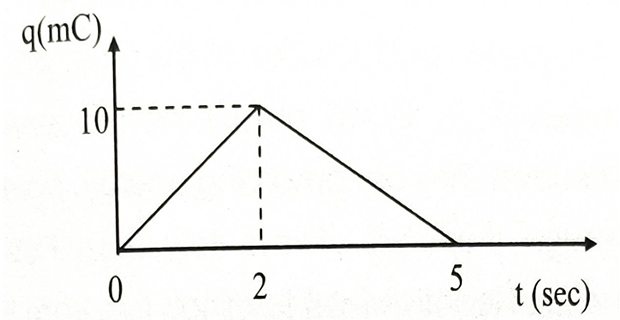
Solution-5

• \[\begin{aligned} &= 10/2 \\ &= 5mA~ \text{[t=0 to 2 sec]} \end{aligned}\]
  Slope of AB
• \[\begin{aligned} &= (10-0)/(2-5) \\ & = -3.33 mA~\text{ [t=2 to 5sec]} \end{aligned}\]
  Slope of BC

Problem-6

• A toaster rated at 1000 W, 240 V is connected to a 220-V supply. Will the toaster be damaged? Will its rating be affected?

Solution-6

• \[\begin{aligned} \mathrm{R} &=\mathrm{V}^{2} / \mathrm{P}=240^{2} / 1000=57.6 \Omega \\ \text { Irating }=\operatorname{Imax} &=\mathrm{P} / \mathrm{V}=1000 / 240=4.167 \mathrm{~A} \end{aligned}\]
  The resistance, and the current rating of the toaster are
• \[\mathrm{I}=\mathrm{V} / \mathrm{R}=220 / 57.6=3.82 \mathrm{~A}\]
  supply, the current drawn is When the toaster is connected to 220 -
• \[P_{1}=220 \mathrm{~V} \times 3.82 \mathrm{~A}=840.4 \mathrm{~W}\]
  This current being less than the current rating, the toaster will not be damaged. The power consumed is

• Thus, the power rating is less than its original power rating.

Problem-7

• What is the maximum voltage that can be applied across the series combination of a 150-\(\Omega\), 2-W resistor and a 100-\(\Omega\), 1-W resistor without exceeding the power rating of either resistor?

Solution-7

• \[\mathrm{I}_{1}=\sqrt{\mathrm{P}} / \mathrm{R}=\sqrt{2} / 150=0.115 \mathrm{~A}\]
  resistor is , the maximum safe current for the From
• \[\mathrm{I}_{2}=\sqrt{\mathrm{P}} / \mathrm{R}=\sqrt{1} / 100=0.1 \mathrm{~A}\]
  resistor is The maximum safe current for the
• \[V_{\text{max}} =\mathrm{I}\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)=0.1 \mathrm{x}(150+100)=\mathbf{2 5} \mathbf{V}\]
  The maximum current cannot exceed the lesser of these two currents. Hence, the maximum voltage that can be applied is

Problem-8

• A wire, 50 m in length and 2 mm\(^2\) in cross section, has a resistance of 0.56 \(\Omega\). A 100-m length of the same wire has a resistance of 2 \(\Omega\) at the same temperature. Find the diameter of this wire.

Solution-8

• \[\begin{array}{lll} & \therefore \rho 1=\rho 2 \\ \mathrm{~L}_{1}=50 \mathrm{~m} & \mathrm{~A}_{1}=2 \mathrm{~mm}^{2} & \mathrm{R}_{1}=0.56 \Omega \\ \mathrm{L}_{2}=100 \mathrm{~m} & \mathrm{~A}_{2}=? & \mathrm{R}_{2}=2 \Omega \end{array}\]
  Given both wires are of same material, so resistivities are same
• \[\begin{aligned} \rho 1 &=\rho 2 \\ \mathrm{R}_{1} \mathrm{~A}_{1} / \mathrm{L}_{1} &=\mathrm{R}_{2} \mathrm{~A}_{2} / \mathrm{L}_{2} \\ (0.56 \mathrm{x} 2) / 50 &=\left(2 \mathrm{x} \mathrm{A}_{2}\right) / 100 \\ \therefore \mathrm{A}_{2} &=1.12 \mathrm{~mm}^{2} \end{aligned}\]
  . So, resistivity We know Resistance
• \[\begin{aligned} 1.12 &=\pi \times \mathrm{d}^{2} / 4 \\ \mathrm{~d}^{2} &=1.42 \\ \therefore \mathrm{d}=& \mathbf{1 . 1 9 m m} \end{aligned}\]
  Area of cross-section

Problem-9

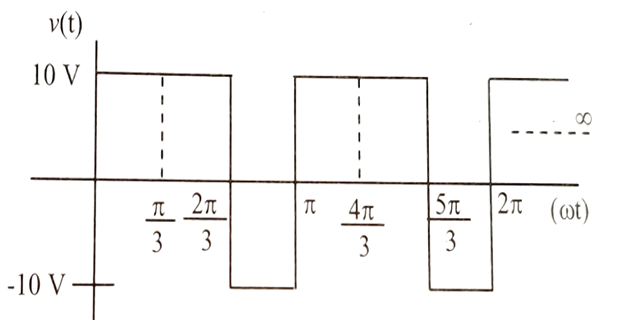
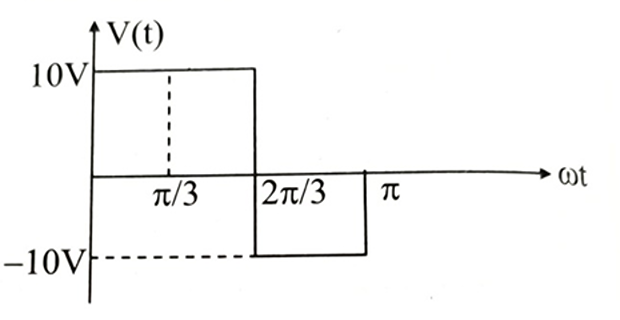
• The voltage across a 10 \(\Omega\) resistor is shown in figure. Average power dissipated by the resistor is