Demonstrative Video
Problem-1
Determine Norton equivalent current and resistance at terminal a-b?
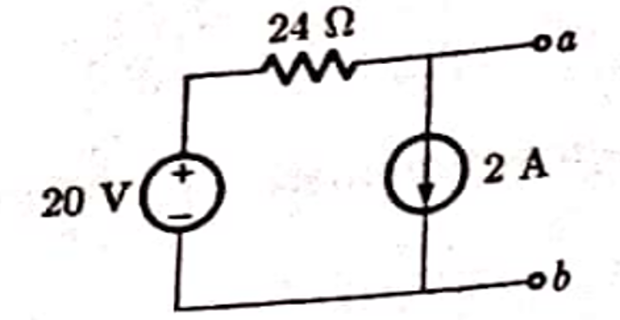
Solution-1
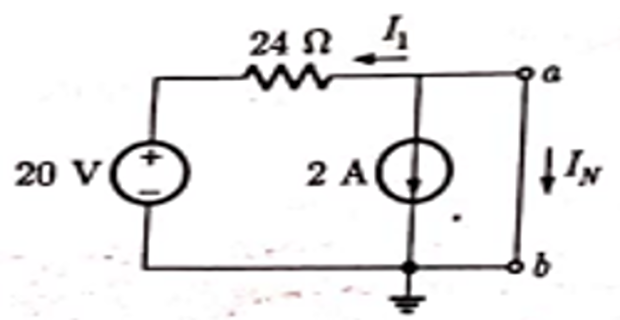
- \[\begin{aligned} I_{N}+I_{1}+2&=0\\ I_{N}-\frac{5}{6}+2 &=0 \\ I_{N} &=-\frac{7}{6} \mathrm{~A} \end{aligned}\]Applying KCL at node
\[R_N=24~\Omega\]
Problem-2
Determine \(V_0\) using Norton’s theorem?
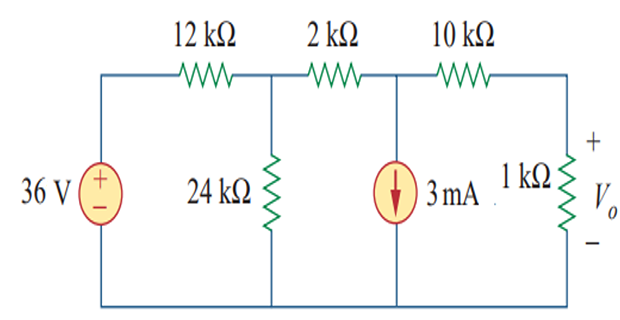
Solution-2
Norton resistance:
\[R_{N} = 10+2+(12||24) = 20~{k\Omega}\]
Norton current:

- \[I_{N} = I_{v}+I_{i}\]Apply superposition theorem by keeping one source active at a time
Considering voltage source only
\[I_{1} = \dfrac{8}{8+12}\times 3 = 1.2~\mbox{mA} \quad 12 || 24 = 8~{k\Omega}\]- \[I_{2} = -1.5~\mbox{mA}\]Considering current source only, we will get parallel equivalent resistance
Norton current \(I_{N}=1.2-1.5=-0.3~\mbox{mA}\)
- \[V_{0} = (1~{k\Omega})\dfrac{20}{20+1}\times (-0.3~\mbox{mA}) = -0.285~\mbox{V}\]Norton equivalent circuit
Problem-3
Determine Norton equivalent current and resistance at terminal a-b?
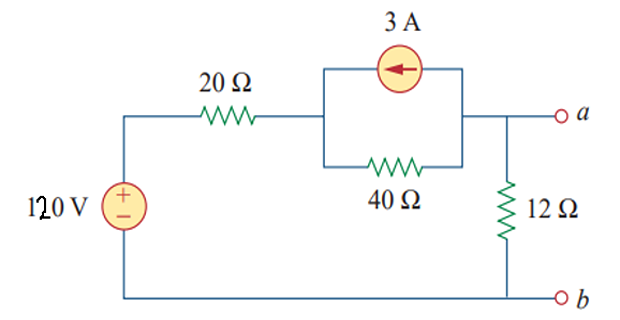
Solution-3
- \[R_{N} = 12 || (20+40) = 10~\Omega\]Determine Norton resistance
- Determine Norton current

- \[\begin{aligned} -120+80+60I_{N}&=0\\ I_{N}&=0.66~A \end{aligned}\]Appling source transformation and KVL
Problem-4
Determine the current \(i\) using Norton equivalent circuit?
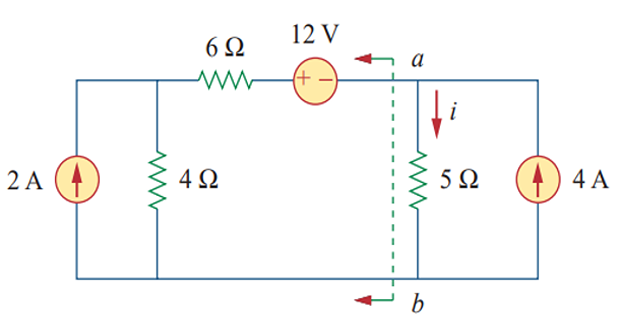
Solution-4
- \[\begin{aligned} R_{N} & = 6+4=10~\Omega\\ 2+(12-v)/6&=v/4 \Rightarrow v = 9.6~V\\ I_{N}&=-(12-v)/6=0.4 \Rightarrow I_{N} = -0.4~A \end{aligned}\]Norton resistance and current
- \[\begin{aligned} i & = \dfrac{10}{10+5}(4-0.4)=2.4~A \end{aligned}\]Combining the RHS circuit to Norton equivalent
Problem-5
Find the Norton equivalent circuit ?
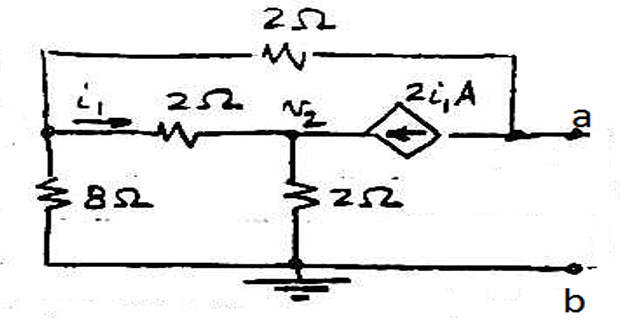
Solution-5
- \[\begin{aligned} \dfrac{v_1}{8}+\dfrac{v_1}{2}+\dfrac{v_1-v_2}{2}&=0 \end{aligned}\]By KCL at node
- \[\begin{aligned} i_1+2i_1&=\dfrac{v_2}{2} \end{aligned}\]By KCL at node
- \[i_1=\dfrac{v_1-v_2}{2}\]Also,
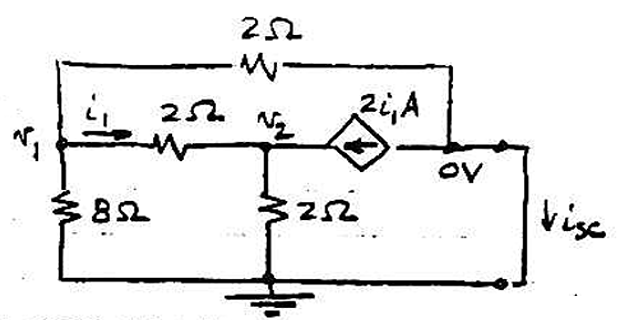
- \[\begin{aligned} v_1&=0~V\\ v_2&=0~V\\ i_{sc} &=\dfrac{v_1}{2}-2i_1=\dfrac{v_1}{2}-2(\dfrac{v_1-v_2}{2})=0~A \end{aligned}\]On solving
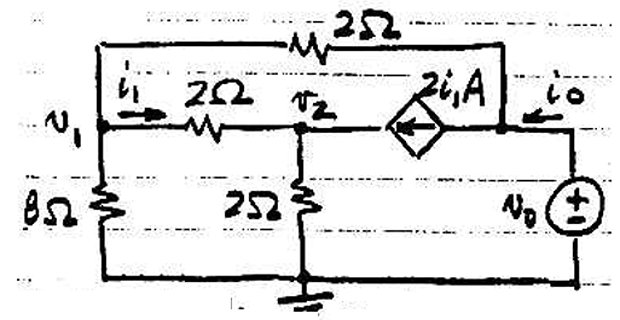

\[R_0 =
\dfrac{v_0}{i_0}=3~\Omega\]