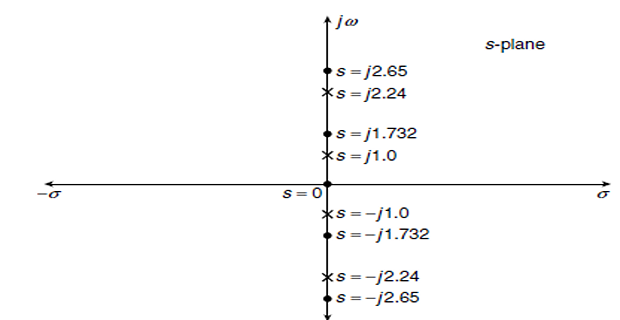Master Circuit Analysis with Transfer Functions

Demonstrative Video

Transfer Function

  • TF is a key concept in signal processing as it indicates how the signal is processed as it passes through the network

  • Vital tool used for numerous circuit analysis

    • fitting tool for finding network response

    • determining or designing network stability

    • used for network synthesis

  • TF of a network describes how the output behaves w.r.t the input

  • It specifies the transfer from the input to the output in the s-domain, assuming no initial energy

  • Definition: The TF \(H(s)\) is the ratio of the output response \(Y(s)\) to the input excitation \(X(s)\), assuming all initial conditions are zero.

\[\boxed{H(s) = \dfrac{Y(s)}{X(s)}}\]

  • The input and output can be either current or voltage at any place in the circuit

  • \[\begin{aligned} H(s)&= \color{magenta}{\textbf{Voltage gain}}=\frac{V_{o}(s)}{V_{i}(s)} \\ H(s)&= \color{blue}{\textbf{Current gain }}=\frac{I_{o}(s)}{I_{i}(s)} \\ H(s)&= \color{red}{\textbf{Impedance }}=\frac{V(s)}{I(s)} \\ H(s)&=\color{purple}{\textbf{Admittance }}=\frac{I(s)}{V(s)} \end{aligned}\]
    There are four possible transfer functions:

  • \(H(s)\) is dimensionless

TF in Circuit Analysis

\[\begin{aligned} Y(s) & = H(s) \cdot X(s) \\ \text{Special case : }~x(t) & = \delta(t)~ \Leftarrow ~ \text{Unit impulse function}\\ \Rightarrow ~ X(s) & = 1\\ \Rightarrow ~ Y(s) & = H(s) ~ \quad ~ \Rightarrow \boxed{y(t) = h(t) = \mathcal{L}^{-1}[H(s)]} \end{aligned}\]

  • \(h(t)\) represents the unit impulse response - Time domain response of the network to a unit impulse.

  • Once we know \(h(t)\) of a network, we can obtain the response of the network to any input signal

Problem

  • The output of a linear system is \(y(t) = 10e^{-t}\cos 4t u(t)\) when the input is \(x(t) = e^{-t}u(t)\). Determine the transfer function and the impulse response of the system ?

Solution :

\[\begin{aligned} x(t) & = e^{-t}u(t) \quad \Rightarrow X(s) = \dfrac{1}{s+1}\\ y(t) & = 10e^{-t} \cos 4t u(t) \quad \Rightarrow Y(s) = \dfrac{10(s+1)}{(s+1)^2+4^2} \\ H(s) & = \dfrac{Y(s)}{X(s)} = \dfrac{10(s^2+2s+1)}{s^2+2s+17} \\ \Rightarrow~h(t) & = 10\delta(t)-40e^{-t}\sin 4t u(t) \end{aligned}\]

Problem

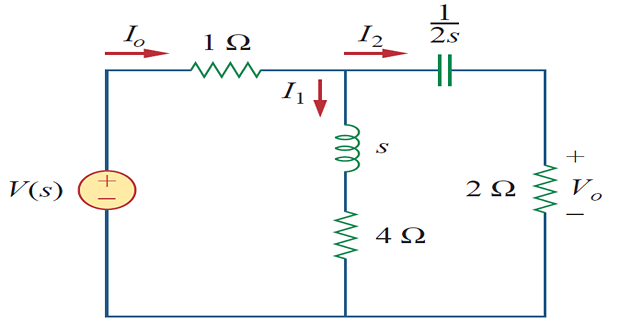
  • Find the transfer function \(H(s) = V_0(s)/I_0(s)\) of the circuit ?

image
\[\begin{gathered} I_{2}=\frac{(s+4) I_{o}}{s+4+2+1 / 2 s} \\ V_{o}=2 I_{2}=\frac{2(s+4) I_{o}}{s+6+1 / 2 s} \\ H(s)=\frac{V_{o}(s)}{I_{o}(s)}=\frac{4 s(s+4)}{2 s^{2}+12 s+1} \end{gathered}\]
Solution:

Poles and Zeros of the TF

  • \[\begin{aligned} \mathbf{F}(s)&=\frac{\mathbf{N}(s)}{\mathbf{D}(s)}=\frac{a_{m} s^{m}+a_{m-1} s^{m-1}+\cdots+a_{1} s+a_{0}}{b_{n} s^{n}+b_{n-1} s^{n-1}+\cdots+b_{1} s+b_{0}} \\ & = \dfrac{K(s-Z_1)(s-Z_2) \cdots (s-Z_{m-1})(s-Z_m)}{(s-P_1)(s-P_2) \cdots (s-P_{n-1})(s-P_n)} \end{aligned}\]
    TF can be represented as

  • \(K = a_m/b_n\)

  • Roots of \(\mathbf{N(s)}=0\) are called the zeros of TF as they make TF = 0

  • Roots of \(\mathbf{D(s)}=0\) are called the poles of TF as they cause TF \(\rightarrow~\infty\)

  • Properties:

    1. If the poles and zeros are not repeated, they are called simple poles and simple zeros, otherwise they are called multiple poles and multiple zeros.

    2. All poles and zeros, if complex, must occur in conjugate pairs.

    3. The real parts of all poles must be negative and any pole on the \(j\omega\)-axis must be simple.

S-plane

  • The zeros and poles are often located in the s-plane

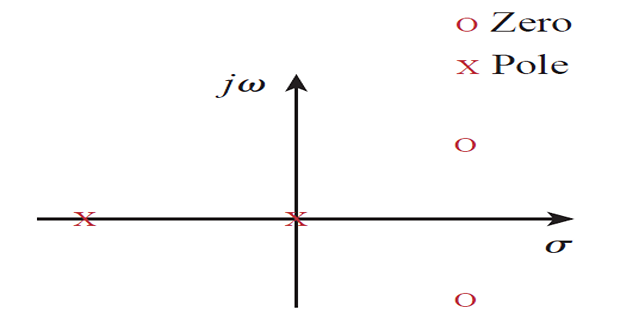
image

  • The location of the roots in the s-plane provides an insight into the nature of the network function and this information is used in network analysis and synthesis.

Problem

\[Z(s)=\frac{s\left(s^{2}+3\right)\left(s^{2}+7\right)}{\left(s^{2}+1\right)\left(s^{2}+5\right)}\]
Draw the pole-zero diagram of the impedance transformed function

Solution:

\[\begin{aligned} & \left(s^{2}+1\right)\left(s^{2}+5\right)=0 \\ & s^{2}=-1 \quad s^{2}=-5 \\ & s=\pm j \quad s=\pm j \sqrt{5} \\ & s=\pm j \quad \pm j 2.24 \end{aligned}\]
\[\begin{aligned} & s\left(s^{2}+3\right)\left(s^{2}+7\right)=0 \\ & s=0, s^{2}=-3 \quad s^{2}=-7 \\ & s=0, \quad s=\pm j \sqrt{3} \quad s=\pm j \sqrt{7} \\ & s=0 \quad \pm j 1.732 \quad \pm j 2.65 \end{aligned}\]
\(=0\) For poles, denominator
image