Demonstrative Video
Balanced Y-Y Connection
- \[\begin{aligned} \mathbf{Z}_{Y} &=\mathbf{Z}_{s}+\mathbf{Z}_{\ell}+\mathbf{Z}_{L} \end{aligned}\]Total impedance
\(\mathbf{Z}_{s}\) and \(\mathbf{Z}_{l}\) are often very small as compared to \(\mathbf{Z}_{L}~\Rightarrow~\) \(\mathbf{Z}_{Y}=\mathbf{Z}_{L}\).
- \[\begin{aligned} \mathbf{V}_{a n} &=V_{p} \angle 0^{\circ} \quad \mathbf{V}_{b n} =V_{p} \angle-120^{\circ}, \quad \mathbf{V}_{c n}=V_{p} \angle+120^{\circ} \end{aligned}\]Assuming positive-sequence:
- \[\begin{aligned} \mathbf{V}_{a b} &=\mathbf{V}_{a n}+\mathbf{V}_{n b}\\ &=\mathbf{V}_{a n}-\mathbf{V}_{b n}=V_{p} \angle 0^{\circ}-V_{p} \angle-120^{\circ} \\ &=V_{p}\left(1+\frac{1}{2}+j \frac{\sqrt{3}}{2}\right)=\sqrt{3} \cdot V_{p} \angle 30^{\circ} \end{aligned}\]Line to Line voltages:
- \[\begin{aligned} &\mathbf{V}_{b c}=\mathbf{V}_{b n}-\mathbf{V}_{c n}=\sqrt{3} V_{p} \angle-90^{\circ} \\ &\mathbf{V}_{c a}=\mathbf{V}_{c n}-\mathbf{V}_{a n}=\sqrt{3} V_{p} \angle-210^{\circ} \end{aligned}\]Similarly,
- \[\begin{aligned} &\boxed{V_{L}=\sqrt{3} V_{p} } \end{aligned}\]\[\begin{aligned} &V_{p}=\left|\mathbf{V}_{a n}\right|=\left|\mathbf{V}_{b n}\right|=\left|\mathbf{V}_{c n}\right| \\ &V_{L}=\left|\mathbf{V}_{a b}\right|=\left|\mathbf{V}_{b c}\right|=\left|\mathbf{V}_{c a}\right| \end{aligned}\]Thus
The line voltages lead their corresponding phase voltages by \(30^{\circ}\)
\[\begin{aligned}
& \mathbf{I}_{a}=\frac{\mathbf{V}_{a n}}{\mathbf{Z}_{Y}} \\
& \mathbf{I}_{b}= \frac{\mathbf{V}_{b
n}}{\mathbf{Z}_{Y}}=\frac{\mathbf{V}_{a n}
\angle-120^{\circ}}{\mathbf{Z}_{Y}}=\mathbf{I}_{a} \angle-120^{\circ} \\
& \mathbf{I}_{c}=\frac{\mathbf{V}_{c n}}{\mathbf{Z}_{Y}}=
\frac{\mathbf{V}_{a n}
\angle-240^{\circ}}{\mathbf{Z}_{Y}}=\mathbf{I}_{a}
\angle-240^{\circ}\\
& \mathbf{I}_{a}+\mathbf{I}_{b}+\mathbf{I}_{c}=0 \\
&
\mathbf{I}_{n}=-\left(\mathbf{I}_{a}+\mathbf{I}_{b}+\mathbf{I}_{c}\right)=0
\\
& \mathbf{V}_{n N}=\mathbf{Z}_{n} \mathbf{I}_{n}=0
\end{aligned}\]
voltage across the neutral wire is zero and
thus can be removed
\[\mathbf{I}_{a}=\frac{\mathbf{V}_{a
n}}{\mathbf{Z}_{Y}}\]
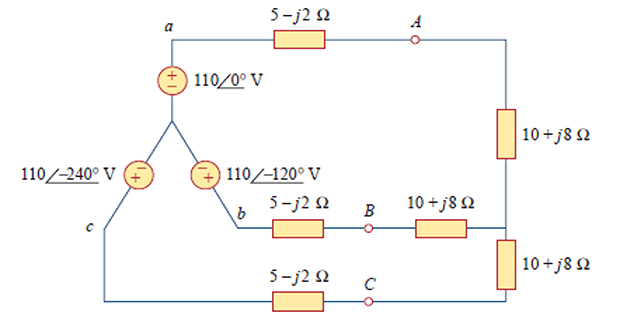
Problem
Calculate the line currents in the three-wire
\[\begin{aligned}
&\mathbf{Z}_{Y}=(5-j 2)+(10+j 8)=15+j 6=16.155 \angle
21.8^{\circ} \\
&\mathbf{I}_{a}=\frac{\mathbf{V}_{a n}}{\mathbf{Z}_{Y}} \\
&\mathbf{I}_{a}=\frac{110 \angle 0^{\circ}}{16.155 \angle
21.8^{\circ}}=6.81 \angle-21.8^{\circ} \mathrm{A} \\
&\mathbf{I}_{b}=\mathbf{I}_{a} \angle-120^{\circ}=6.81
\angle-141.8^{\circ} \mathrm{A} \\
&\mathbf{I}_{c}=\mathbf{I}_{a} \angle-240^{\circ}=6.81
\angle-261.8^{\circ} \mathrm{A}=6.81 \angle 98.2^{\circ} \mathrm{A}
\end{aligned}\]
Balanced Y-Delta Connection
\[\begin{aligned}
\mathbf{V}_{a n}&=V_{p} \angle 0^{\circ} \\
\mathbf{V}_{b n}&=V_{p} \angle-120^{\circ}\\
\mathbf{V}_{c n}&=V_{p} \angle+120^{\circ} \\
\mathbf{V}_{ab}&=\sqrt{3} V_{p} \angle 30^{\circ} =
\mathbf{V}_{AB} \\
\mathbf{V}_{bc}&=\sqrt{3} V_{p} \angle -90^{\circ} =
\mathbf{V}_{BC} \\
\mathbf{V}_{ca}&=\sqrt{3} V_{p} \angle -150^{\circ} =
\mathbf{V}_{CA}
\end{aligned}\]
\[\begin{aligned}
\mathbf{I}_{A B}&=\frac{\mathbf{V}_{A
B}}{\mathbf{Z}_{\Delta}}, \quad \mathbf{I}_{B C}=\frac{\mathbf{V}_{B
C}}{\mathbf{Z}_{\Delta}}, \quad \mathbf{I}_{C A}=\frac{\mathbf{V}_{C
A}}{\mathbf{Z}_{\Delta}} \\
& -\mathbf{V}_{a n}+\mathbf{Z}_{\Delta} \mathbf{I}_{A
B}+\mathbf{V}_{b n}=0
\end{aligned}\]
\[\begin{aligned}
\text { Since } \mathbf{I}_{C A}& =\mathbf{I}_{A
B}\angle-240^{\circ} \\
\mathbf{I}_{a}& =\mathbf{I}_{A B}-\mathbf{I}_{C
A}=\mathbf{I}_{A B}\left(1-1 \angle-240^{\circ}\right) \\
=& \mathbf{I}_{A B}(1+0.5-j 0.866)\\
=&\mathbf{I}_{A B} \sqrt{3} \angle-30^{\circ} \\
&\boxed{I_{L}=\sqrt{3} I_{p}} \\
I_{L}&=\left|\mathbf{I}_{a}\right|=\left|\mathbf{I}_{b}\right|=\left|\mathbf{I}_{c}\right|
\\
I_{p}&=\left|\mathbf{I}_{A B}\right|=\left|\mathbf{I}_{B
C}\right|=\left|\mathbf{I}_{C A}\right|
\end{aligned}\]
\[\mathbf{Z_Y} = \dfrac{
\mathbf{Z}_\Delta}{3}\]
Problem
A balanced abc-sequence Y-connected source with \(V_{an} = 100 \angle 10^{\circ}\) V is connected to a \(\Delta\)-connected balanced load \(\left(8+j4\right)~\Omega\) per phase. Calculate the phase and line currents.
\[\mathbf{Z}_{\Delta}=8+j
4=8.944 \angle 26.57^{\circ} \Omega\]
The phase currents are or ,
then the line voltage is If the phase voltage METHOD 1:
\[\begin{aligned}
\mathbf{I}_{a}&=\mathbf{I}_{A B} \sqrt{3}
\angle-30^{\circ}=\sqrt{3}(19.36) \angle 13.43^{\circ}-30^{\circ} \\
&=33.53 \angle-16.57^{\circ} \mathrm{A} \\
\mathbf{I}_{b}&=\mathbf{I}_{a} \angle-120^{\circ}=33.53
\angle-136.57^{\circ} \mathrm{A} \\
\mathbf{I}_{c}&=\mathbf{I}_{a} \angle+120^{\circ}=33.53
\angle 103.43^{\circ} \mathrm{A}
\end{aligned}\]
The line currents are
\[\mathbf{I}_{a}=\frac{\mathbf{V}_{a
n}}{\mathbf{Z}_{\Delta} / 3}=\frac{100 \angle 10^{\circ}}{2.981 \angle
26.57^{\circ}}=33.54 \angle-16.57^{\circ} \mathrm{A}\]
phase sequence. as above.
Other line currents are obtained using the METHOD 2:
Balanced Delta-Delta Connection
\[\begin{aligned}
&\mathbf{V}_{a b}=V_{p} \angle 0^{\circ} \quad \mathbf{V}_{b
c}=V_{p} \angle-120^{\circ}, \quad \mathbf{V}_{c a}=V_{p}
\angle+120^{\circ}\\
&\mathbf{V}_{a b}=\mathbf{V}_{A B}, \quad \mathbf{V}_{b
c}=\mathbf{V}_{B C}, \quad \mathbf{V}_{c a}=\mathbf{V}_{C A}\\
&\mathbf{I}_{A B}=\frac{\mathbf{V}_{A
B}}{Z_{\Delta}}=\frac{\mathbf{V}_{a b}}{Z_{\Delta}}, \quad \mathbf{I}_{B
C}=\frac{\mathbf{V}_{B C}}{Z_{\Delta}}=\frac{\mathbf{V}_{b
c}}{Z_{\Delta}} \quad \mathbf{I}_{C A}=\frac{\mathbf{V}_{C
A}}{Z_{\Delta}}=\frac{\mathbf{V}_{c a}}{Z_{\Delta}}\\
&\mathbf{I}_{a}=\mathbf{I}_{A B}-\mathbf{I}_{C A},
\quad \mathbf{I}_{b}=\mathbf{I}_{B C}-\mathbf{I}_{A B},
\quad \mathbf{I}_{C}=\mathbf{I}_{C A}-\mathbf{I}_{B C}
\end{aligned}\]
\(I_L = \sqrt{3}I_p\)
each line current lags the corresponding phase current by \(30^{\circ}\)
Problem
A balanced \(\Delta\)-connected load having an impedance \(20-j 15 \Omega\) is connected to a \(\Delta\)-connected, positive-sequence generator having \(\mathbf{V}_{a b}=330 \angle 0^{\circ} \mathrm{V}\). Calculate the phase currents of the load and the line currents.
Solution:
\[\mathbf{Z}_{\Delta}=20-j 15=25
\angle-36.87^{\circ} \Omega\]
\[\begin{aligned}
\mathbf{I}_{A B}&=\frac{\mathbf{V}_{A
B}}{\mathbf{Z}_{\Delta}}=\frac{330 \angle 0^{\circ}}{25
\angle-36.87}=13.2 \angle 36.87^{\circ} \mathrm{A} \\
\mathbf{I}_{B C}&=\mathbf{I}_{A B} \angle-120^{\circ}=13.2
\angle-83.13^{\circ} \mathrm{A} \\
\mathbf{I}_{C A}&=\mathbf{I}_{A B} \angle+120^{\circ}=13.2
\angle 156.87^{\circ} \mathrm{A}
\end{aligned}\]
\(\mathbf{V}_{A B}=\mathbf{V}_{a b}\)The load impedance per phase is
\[\begin{aligned}
\mathbf{I}_{a}&=\mathbf{I}_{A B} \sqrt{3}
\angle-30^{\circ}=\left(13.2 \angle 36.87^{\circ}\right)\left(\sqrt{3}
\angle-30^{\circ}\right)\\
&= 2 2 . 8 6 \angle { 6 . 8 7 ^ { \circ } } \mathrm { A }\\
\mathbf{I}_{b}&=\mathbf{I}_{a} \angle-120^{\circ}=22.86
\angle-113.13^{\circ} \mathrm{A}\\
\mathbf { I } _ { c } &= \mathbf { I } _ { a } \angle + 1 2
0 ^ { \circ } = 2 2 . 8 6 \angle { 1 2 6 . 8 7 ^ { \circ } \mathrm { A }
}
\end{aligned}\]
The line currents are
Balanced Delta-Star Connection
\[\begin{aligned}
&\mathbf{V}_{a b}=V_{p} \angle 0^{\circ}, \quad \mathbf{V}_{b
c}=V_{p} \angle-120^{\circ} \quad \mathbf{V}_{c a}=V_{p}
\angle+120^{\circ} \\
& \text{KVL}~-\mathbf{V}_{a b}+\mathbf{Z}_{Y}
\mathbf{I}_{a}-\mathbf{Z}_{Y} \mathbf{I}_{b}=0 \\
\Rightarrow &
\mathbf{Z}_{Y}\left(\mathbf{I}_{a}-\mathbf{I}_{b}\right)=\mathbf{V}_{a
b}=V_{p} \angle 0^{\circ} \\
\Rightarrow & \mathbf{I}_{a}-\mathbf{I}_{b}=\frac{V_{p}
\angle 0^{\circ}}{\mathbf{Z}_{Y}} \\
& \mathbf{I}_{a}-\mathbf{I}_{b}=\mathbf{I}_{a}\left(1-1
\angle-120^{\circ}\right) \\
= & \mathbf{I}_{a}\left(1+\frac{1}{2}+j
\frac{\sqrt{3}}{2}\right)=\mathbf{I}_{a} \sqrt{3} \angle 30^{\circ} \\
& \mathbf{I}_{a}=\frac{V_{p} / \sqrt{3}
\angle-30^{\circ}}{\mathbf{Z}_{Y}} \quad \mathbf{I}_{b} =
\mathbf{I}_{a}\angle -120^{\circ} \quad \mathbf{I}_{c}
= \mathbf{I}_{a} \angle +120^{\circ}
\end{aligned}\]
Summary
Assuming abc-phase sequence
| Connection | Phase | Line |
|---|---|---|
| Y-Y | \(\begin{aligned} V_{an} & =V_{p}\angle0^{\circ}\\ V_{bn} & =V_{p}\angle-120^{\circ}\\ V_{cn} & =V_{p}\angle+120^{\circ} \end{aligned}\) | \(\begin{aligned} V_{ab} & =\sqrt{3}V_{p}\angle30^{\circ}\\ V_{bc} & =V_{ab}\angle-120^{\circ}\\ V_{ca} & =V_{ab}\angle+120^{\circ} \end{aligned}\) |
| Same Line current | \(\begin{aligned} I_{a} & =V_{an}/Z_{Y}\\ I_{b} & =I_{a}\angle-120^{\circ}\\ I_{c} & =I_{a}\angle+120^{\circ} \end{aligned}\) | |
| Y-\(\Delta\) | \(\begin{aligned} V_{an} & =V_{p}\angle0^{\circ}\\ V_{bn} & =V_{p}\angle-120^{\circ}\\ V_{cn} & =V_{p}\angle+120^{\circ} \end{aligned}\) | \(\begin{aligned} V_{ab} & =\sqrt{3}V_{p}\angle30^{\circ}\\ V_{bc} & =V_{ab}\angle-120^{\circ}\\ V_{ca} & =V_{ab}\angle+120^{\circ} \end{aligned}\) |
| \(\begin{aligned} I_{AB} & =V_{AB}/Z_{\Delta}\\ I_{BC} & =V_{BC}/Z_{\Delta}\\ I_{CA} & =V_{CA}/Z_{\Delta} \end{aligned}\) | \(\begin{aligned} I_{a} & =I_{AB}\sqrt{3}\angle-30^{\circ}\\ I_{b} & =I_{a}\angle-120^{\circ}\\ I_{c} & =I_{a}\angle+120^{\circ} \end{aligned}\) | |
| \(\Delta-\Delta\) | \(\begin{aligned} V_{ab} & = V_p\angle 0^{\circ} \\ V_{bc} & = V_p\angle -120^{\circ} \\ V_{ca} & = V_p\angle +120^{\circ} \end{aligned}\) | Same as phase |
| \(\begin{aligned} I_{AB} & = V_{ab}/Z_{\Delta} \\ I_{BC} & = V_{bc}/Z_{\Delta} \\ I_{CA} & = V_{ca}/Z_{\Delta} \end{aligned}\) | \(\begin{aligned} I_{a} & = I_{AB}\sqrt{3}\angle{-30^{\circ}} \\ I_{b} & = I_{a}\angle{-120^{\circ}} \\ I_{c} & = I_{c}\angle{+120^{\circ}} \end{aligned}\) | |
| \(\Delta\)-Y | \(\begin{aligned} V_{ab} & = V_p \angle{0^{\circ}}\\ V_{bc} & = V_p \angle{-120^{\circ}}\\ V_{ca} & = V_p \angle{+120^{\circ}}\\ \end{aligned}\) | Same as phase |
| Same as line | \(\begin{aligned} I_a & = \dfrac{V_p\angle -30^{\circ}}{\sqrt{3}Z_{Y}} \\ I_b & = I_a \angle -120^{\circ}\\ I_c & = I_a \angle +120^{\circ} \end{aligned}\) |