Demonstrative Video
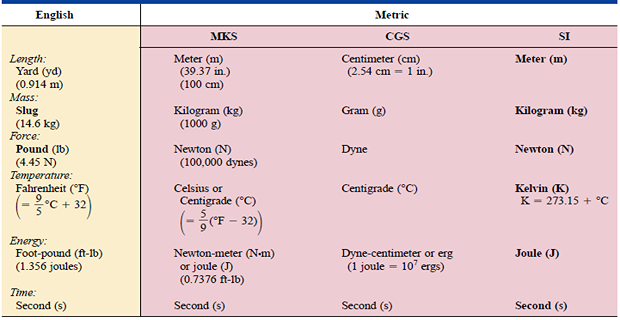
System of Units
In the past, most commonly used were the English and Metric
English system is based on a single standard, the metric is subdivided into two interrelated standards: the MKS and the CGS
MKS system uses Meters, Kilograms, and Seconds, while the CGS system uses Centimeters, Grams, and Seconds.
Need for a standard set of units to be adopted by all nations has become increasingly obvious.
In 1960, the General Conference held by International Bureau of Weights and Measures located at France, adopted a system called Le Système International d’Unités (International System of Units), which has the international abbreviation SI.
Comparison of system of Units

| Physical quantity | Symbol | Unit | Symbol | Measuring device |
| Current | I | Ampere | A | Amperemeter |
| Voltage | U | Volt | V | Voltmeter |
| Power | P | Watt | W | Powermeter |
| Resistance | R | Ohm | \(\Omega\) | Ohmmeter |
| Capacitance | C | Farad | F | Capacitance meter |
| Inductance | L | Henry | H | Inductance meter |
| Frequency | f | Hertz | Hz | Oscilloscope |
| Period | T | Second | S | Oscilloscope |
| Charge | Q | Coulomb | C | Charge meter |
| Conductance | G | Siemens | S | Conductivity meter |
| Name | Symbol | Base equivalent |
| Volt | V | \(kg \cdot m^2 \cdot s^{-3} \cdot A^{-1}\) |
| Watt | W | \(kg \cdot m^2 \cdot s^{-3}\) |
| Ohm | \(\Omega\) | \(kg \cdot m^2 \cdot s^{-3} \cdot A^{-2}\) |
| Farad | F | \(kg^{-1} \cdot m^{-2} \cdot s^{4} \cdot A^{2}\) |
| Henry | H | \(kg \cdot m^2 \cdot s^{-2} \cdot A^{-2}\) |
| Hertz | Hz | \(s^{-1}\) |
| Coulomb | C | \(A \cdot s\) |
| Siemens | S | \(kg^{-1} \cdot m^{-2}\cdot s^{3} \cdot A^{2}\) |
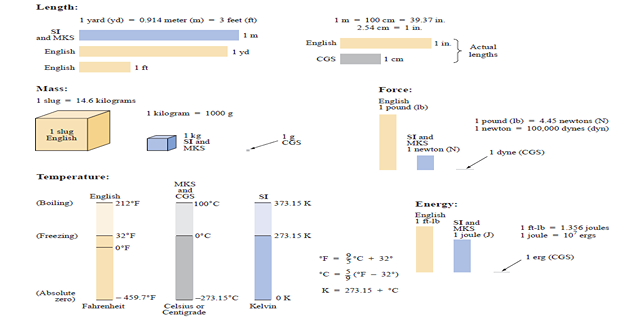
Comparison of various Units
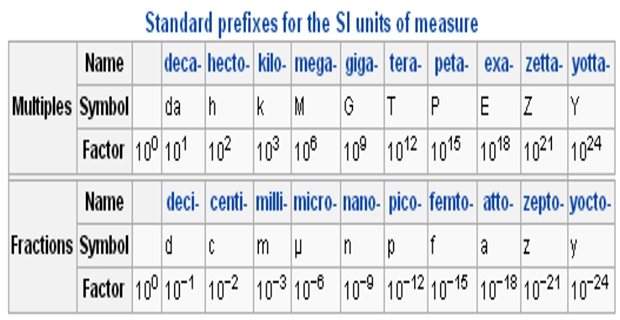
Power of 10
Relative magnitude of the various units of measurement very large and very small numbers will frequently be encountered
To ease the difficulty of mathematical operations with numbers of such varying size, powers of ten are usually employed
\(10000 = 10^{+4}~\Rightarrow\) count number of zeros
\(0.00001 = 10^{-5}~\Rightarrow\) zeros+1
\(10^{n} = \dfrac{1}{10^{-n}}\)
Basic Arithmetic Operation of Power of 10
- \[A \times 10^{n} \pm B \times 10^{n} = \left(A\pm B\right) \times 10^{n}\]Addition and Subtraction
- \[\left(A\times 10^{n}\right)\left(B\times 10^{m}\right) = (A)(B)\times 10^{n+m}\]Multiplication
- \[\dfrac{A\times 10^{n}}{B\times 10^{m}} = \dfrac{A}{B} \times 10^{n-m}\]Division
- \[\left(A\times 10^{n}\right)^{m} = A^{m} \times 10^{nm}\]Powers
Fixed-Point, Floating-Point, Scientific, & Engineering Notation
If powers of ten are not employed, they are written in the fixed-point or floating-point notation.
The fixed-point format requires that the decimal point appear in the same place each time.
In the floating-point format, the decimal point will appear in a location defined by the number to be displayed.
- \[\frac{1}{3}=0.333 \quad \frac{1}{16}=0.063 \quad \frac{2300}{2}=1150.000\]Fixed-point with thousandths place accuracy:
- \[\frac{1}{3}=0.333333333333 \quad \frac{1}{16}=0.0625 \quad \frac{2300}{2}=1150\]Floating point format:
Scientific (also called standard) notation and engineering notation make use of powers of ten with restrictions on the mantissa (multiplier) or scale factor (power of the power of ten).
Scientific notation requires that the decimal point appear directly after the first digit greater than or equal to 1 but less than 10.
- \[\frac{1}{3}=3.33333333333 \mathrm{E}-1 \quad \frac{1}{16}=6.25 \mathrm{E}-2 \quad \frac{2300}{2}=1.15 \mathrm{E} 3\]Within the scientific notation, the fixed- or floating-point format can be chosen.
- \[\frac{1}{3}=333.333333333 \mathrm{E}-3 \quad \frac{1}{16}=62.5 \mathrm{E}-3 \quad \frac{2300}{2}=1.15 \mathrm{E} 3\]Engineering notation specifies that all powers of ten must be multiples of 3, and the mantissa must be greater than or equal to 1 but less than 1000
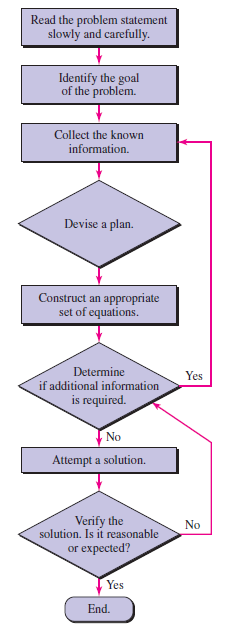
SUCCESSFUL PROBLEM-SOLVING STRATEGIES