Series Resonance in RLC Circuit

Demonstrative Video

Resonance

  • Feature of the frequency response of a circuit \(\Rightarrow\) sharp peak (or resonant peak) exhibited in its amplitude characteristic.

  • System that has a complex conjugate pair of poles; cause of oscillations of stored energy from one form to another.

  • Allows frequency discrimination in communications networks.

  • Occurs in any circuit that has at least one \(L\) and one \(C\).

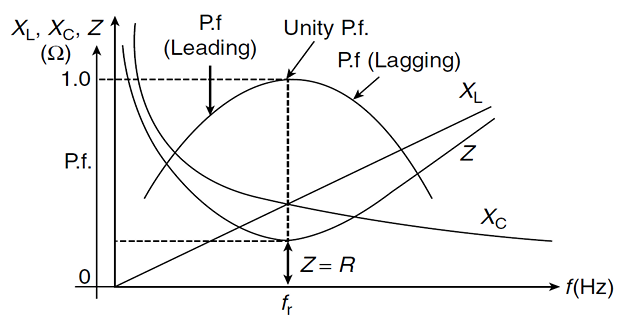
  • Resonance : condition in an RLC circuit in which the \(|X_C|= |X_L|\), thereby resulting in a purely resistive impedance.

  • Resonant circuits (series or parallel) are useful for constructing filters, as their TFs can be highly frequency selective.

  • Used in many applications such as selecting the desired stations in radio and TV receivers.

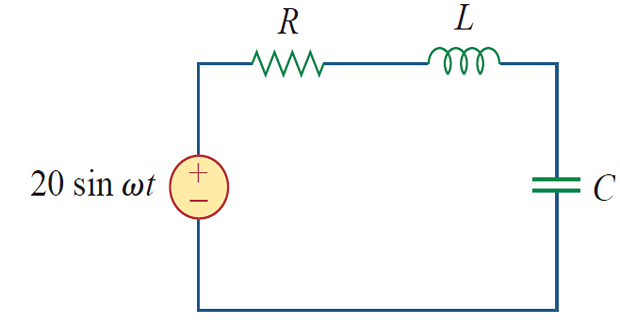
Series Resonance

\[\begin{aligned} \mathbf{Z}=\mathbf{H}(\omega) &=\frac{\mathbf{V}_{s}}{\mathbf{I}}=R+j \omega L+\frac{1}{j \omega C} \\ \mathbf{Z} &=R+j\left(\omega L-\frac{1}{\omega C}\right) \\ \operatorname{Im}(\mathbf{Z}) &=\omega L-\frac{1}{\omega C}=0 \end{aligned}\]

  • Resonant frequency \(\omega_0\) : at which \(\mathbf{Z}\) of the circuit is purely real

\[\begin{aligned} X_L & = X_C \\ \Rightarrow~ \omega_{0} L &=\frac{1}{\omega_{0} C} \\ \end{aligned}\]
\[\boxed{\omega_{0} =\frac{1}{\sqrt{L C}} \mathrm{rad} / \mathrm{s} } \quad \boxed{f_{0} =\frac{1}{2 \pi \sqrt{L C}} \mathrm{~Hz}}\]

At resonance:

  • \(\mathbf{Z} = R~\Rightarrow\) \(LC\) series acts as SC and the entire \(\mathbf{V_s}\) is across \(R\)

  • \(\mathbf{V_s}\) and \(\mathbf{I}\) in phase \(\Rightarrow\) PF is unity

  • \(\mathbf{H(\omega)} = \mathbf{Z(\omega)}\) minimum

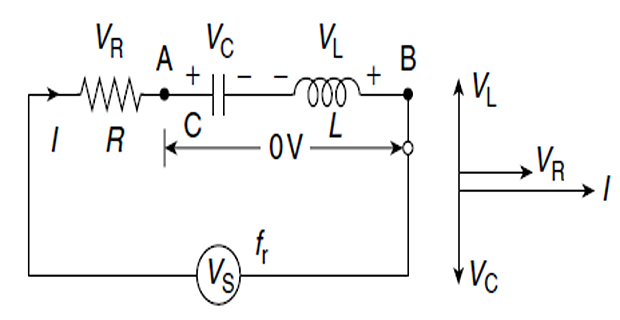
  • \[\begin{aligned} \left|\mathbf{V}_{L}\right| &=\frac{V_{m}}{R} \omega_{0} L=Q V_{m} \\ \left|\mathbf{V}_{C}\right| &=\frac{V_{m}}{R} \frac{1}{\omega_{0} C}=Q V_{m} \end{aligned}\]
    is Quality factor \(\mathbf{V_s}\)\(\mathbf{V_C}\)\(\mathbf{V_L}\)

series resonant circuit also called voltage resonant circuit

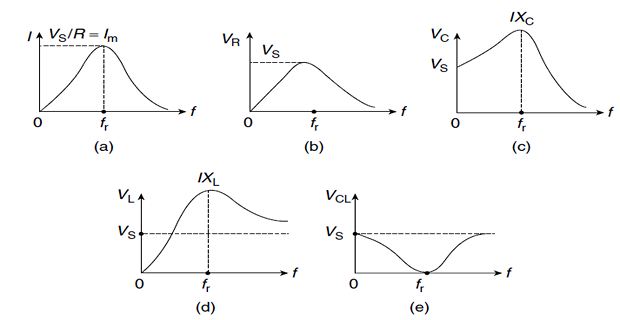
image

image
image
\[X_L = \omega L \qquad X_C = \dfrac{1}{\omega C}\]
\[\begin{aligned} & |\mathbf{I}|=\frac{V_{m}}{\sqrt{R^{2}+(\omega L-1 / \omega C)^{2}}} \\ & \text{Avg. power dissipated}~P(\omega)=\frac{1}{2} I^{2} R \\ & \text{Max. power dissipated}~P\left(\omega_{0}\right)=\frac{1}{2} \frac{V_{m}^{2}}{R} \end{aligned}\]

  • At certain \(\omega = \omega_1, \omega_2\) the dissipated power is half the max. value.

  • Known as Half-power frequencies

\[\begin{aligned} &P\left(\omega_{1}\right)=P\left(\omega_{2}\right)=\frac{\left(V_{m} / \sqrt{2}\right)^{2}}{2 R}=\frac{V_{m}^{2}}{4 R} \\ &\text{Setting}~\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}=\sqrt{2} R \end{aligned}\]
  • \[\omega_0 = \sqrt{\omega_1 \cdot \omega_2}\]
    Resonant frequency is the geometric mean of the half-power frequencies

  • \(\omega_1, \omega_2\) are not symmetrical around \(\omega_0\) because frequency response is not symmetrical, however it is often a reasonable approximation

  • \[\textbf{Bandwidth}~B = \omega_2 - \omega_1\]
    \(B\)width\(R\)Height

  • Quality factor : Quantitate measurement of the sharpness of the resonance in a resonance circuit

    \[Q=2 \pi \frac{\text { Peak energy stored in the circuit }}{\begin{array}{c} \text { Energy dissipated by the circuit } \\ \text { in one period at resonance } \end{array}}\]
\[\begin{aligned} Q&=\frac{\text { energy stored }}{\text { energy dissipated }} \\ &=\frac{\text { reactive power }}{\text { True or active power }} = \frac{I^{2} X_{\mathrm{L}}}{I^{2} R} =\frac{X_{\mathrm{L}}}{R}\\ &\boxed{Q=\frac{\omega_{0} L}{R}=\frac{1}{\omega_{0} C R}}\\ &\boxed{B=\frac{R}{L}=\frac{\omega_{0}}{Q}}\quad =\omega_{0}^{2} C R \end{aligned}\]
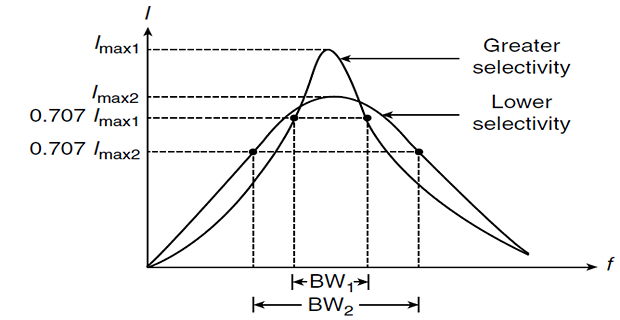
image

\(\boxed{Q~\uparrow~\Rightarrow~B~\downarrow}\)

  • \(Q\) of a resonant circuit is the ratio of its \(\omega_0\) to its \(B\)

  • RLC circuit selectivity is the ability to respond to a certain frequency and discriminate against all other frequencies.

  • Frequency band to be selected or rejected is narrow, \(Q\) must be high.

  • If the band of frequencies is wide, \(Q\) must be low.

  • High-\(Q\) circuits \(\Rightarrow\) \(Q \geq 10\)

  • \[\omega_{1} \simeq \omega_{0}-\frac{B}{2}, \quad \omega_{2} \simeq \omega_{0}+\frac{B}{2}\]
    For all practical purpose

  • High-Q circuits are used often in communications networks

  • Resonant circuit is characterized by five related parameters: \(\omega_0, \omega_1, \omega_2, Q, B\)

Problem

Given: \(R=2~\Omega,~L=1~\mathrm{mH},~C=0.4~\mathrm{\mu F}\). Determine

  • \(\omega_{0}, ~\omega_{1,2},~Q, ~B\)

  • Amplitude of the current at \(\omega_0, \omega_1, \omega_2\)

image

Solution

\[\omega_0 =\frac{1}{\sqrt{L C}}=50 \mathrm{krad} / \mathrm{s}\]
\[\begin{aligned} \omega_{1} &=-\frac{R}{2 L}+\sqrt{\left(\frac{R}{2 L}\right)^{2}+\frac{1}{L C}} \\ &=-1+\sqrt{1+2500} =49 \mathrm{krad} / \mathrm{s} \\ \omega_{2} &=1+\sqrt{1+2500}=51 \mathrm{krad} / \mathrm{s} \\ B &=\omega_{2}-\omega_{1}=2 \mathrm{krad} / \mathrm{s} \\ \text{or}~B &=\frac{R}{L}=\frac{2}{10^{-3}}=2 \mathrm{krad} / \mathrm{s} \\ Q &=\frac{\omega_{0}}{B}=\frac{50}{2}=25 \end{aligned}\]
Method-1
\[\begin{aligned} \omega=\omega_{0},~\Rightarrow \quad I&=\frac{V_{m}}{R}=\frac{20}{2}=10 \mathrm{~A} \\ \omega=\omega_{1}, \omega_{2}, ~\Rightarrow \quad I&=\frac{V_{m}}{\sqrt{2} R}=\frac{10}{\sqrt{2}}=7.071 \mathrm{~A} \end{aligned}\]