Power Factor Correction

Demonstrative Video

Conservation of AC Power

  • The principle of conservation of power applies to ac as well as to dc circuits

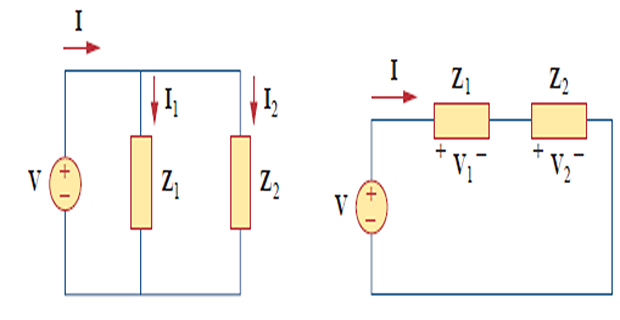
image
\[\begin{aligned} \mathbf{I} &=\mathbf{I}_{1}+\mathbf{I}_{2} \\ \mathbf{S} &=\mathbf{V I}^{*} \\ &=\mathbf{V}\left(\mathbf{I}_{1}^{*}+\mathbf{I}_{2}^{*}\right) \\ &=\mathbf{V I}_{1}^{*}+\mathbf{V I}_{2}^{*} \\ &=\mathbf{S}_{1}+\mathbf{S}_{2} \end{aligned}\]
\[\boxed{\mathbf{S} =\mathbf{S}_{1}+\mathbf{S}_{2}+\cdots+\mathbf{S}_{N}}\]

  • The complex, real, and reactive powers of the sources equal the respective sums of the \(\mathbf{S}\), \(\mathbf{P}\), and \(\mathbf{Q}\) powers of the individual loads.

Problem

\[\begin{aligned} \mathbf{Z} &=(4+j 2)+(15-j 10)\\ &=19-j 8=20.62 \angle-22.83^{\circ} \Omega \\ \mathbf{I} &=\frac{\mathbf{V}_{s}}{\mathbf{Z}}=\frac{220 \angle 0^{\circ}}{20.62 \angle-22.83^{\circ}}\\ &=10.67 \angle 22.83^{\circ} \mathrm{A} \end{aligned}\]
\[\begin{aligned} \mathbf{S}_{s} &=\mathbf{V}_{s} \mathbf{I}^{*}=\left(220 \angle 0^{\circ}\right)\left(10.67 \angle-22.83^{\circ}\right) \\ &=2347.4 \angle-22.83^{\circ}=(2163.5-j 910.8) \mathrm{VA}\\ \Rightarrow~\mathbf{P} & = 2163.5 \mathrm{~W} \qquad \mathbf{Q} = 910.8~ \mathrm{~VAR (leading)}. \end{aligned}\]
\[\begin{aligned} \mathbf{V}_{L}=(15-j 10) \mathbf{I} &=\left(18.03 \angle -33.7^{\circ}\right)\left(10.67 \angle 22.83^{\circ}\right) \\ &=192.38 \angle -10.87^{\circ} \mathrm{V} \mathrm{rms} \end{aligned}\]
\[\begin{aligned} \mathbf{S}_{L}=\mathbf{V}_{L} \mathbf{I}^{*} &=\left(192.38 \angle -10.87^{\circ}\right)\left(10.67 \angle -22.83^{\circ}\right) \\ &=2053 \angle-33.7^{\circ}=(1708-j 1139) \mathrm{VA}\\ \Rightarrow~\mathbf{P} & = 1708 \mathrm{~W} \qquad \mathbf{Q} = 1139~ \mathrm{~VAR (leading)}. \end{aligned}\]
For the load, the voltage is

  • Note : \(\mathbf{S}_{s}=\mathbf{S}_{\text {line }}+\mathbf{S}_{L}\), as expected.

  • We have used the rms values of voltages and currents.

Power Factor Correction

  • Most domestic loads (washing machines, air conditioners, and refrigerators) and industrial loads ( induction motors) are inductive and operate at a low lagging power factor.

  • Although the inductive nature of the load cannot be changed, we can increase its power factor.

  • The process of increasing the PF without altering the voltage or current to the original load is known as power factor correction.

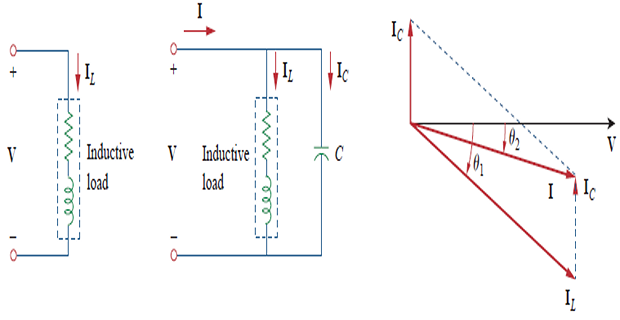
image

  • Adding \(C~\Rightarrow\) phase angle reduce from \(\theta_1\) to \(\theta_2~\Rightarrow\) PF \(\uparrow\).

  • With same \(\mathbf{V}\) current decreases \(\Rightarrow\) less electricity bill.

\[\begin{aligned} P &=S_{1} \cos \theta_{1} \\ Q_{1} &=S_{1} \sin \theta_{1}=P \tan \theta_{1} \\ Q_{2} &=P \tan \theta_{2} \\ Q_{C} &=Q_{1}-Q_{2}=P\left(\tan \theta_{1}-\tan \theta_{2}\right) \\ Q_{C} &=V_{\mathrm{rms}}^{2} / X_{C}=\omega C V_{\mathrm{rms}}^{2} \end{aligned}\]
\[\begin{aligned} C &=\frac{Q_{C}}{\omega V_{\mathrm{rms}}^{2}}=\frac{P\left(\tan \theta_{1}-\tan \theta_{2}\right)}{\omega V_{\mathrm{rms}}^{2}} \\ Q_{L} &=\frac{V_{\mathrm{rms}}^{2}}{X_{L}}=\frac{V_{\mathrm{rms}}^{2}}{\omega L} \Rightarrow L=\frac{V_{\mathrm{rms}}^{2}}{\omega Q_{L}} \\ Q_{L} &=Q_{1}-Q_{2} \end{aligned}\]

Problem

  • When connected to a 120-V (rms), 60-Hz power line, a load absorbs 4 kW at a lagging power factor of 0.8. Find the value of capacitance necessary to raise the pf to 0.95.

  • \[\begin{aligned} \mathrm{pf}=0.8 \Rightarrow \cos \theta_{1}=0.8 \quad \Rightarrow \quad \theta_{1}=36.87^{\circ} \end{aligned}\]
    Solution:
  • \[\begin{aligned} S_{1}&=\frac{P}{\cos \theta_{1}}=\frac{4000}{0.8}=5000 \mathrm{VA}\\ Q_{1}&=S_{1} \sin \theta=5000 \sin 36.87=3000 \mathrm{VAR}\\ \cos \theta_{2}&=0.95 \quad \Rightarrow \quad \theta_{2}=18.19^{\circ} \end{aligned}\]
    We obtain the apparent power from the real power and the pf as
  • \[S_{2}=\frac{P}{\cos \theta_{2}}=\frac{4000}{0.95}=4210.5 \mathrm{VA}\]
    has not changed. But the apparent power has changed; its new value is , The real power is raised to When the
  • \[Q_{2}=S_{2} \sin \theta_{2}=1314.4 \mathrm{VAR}\]
    The new reactive power is

  • The difference between the new and old reactive powers is due to the parallel addition of the capacitor to the load.

  • \[Q_{C}=Q_{1}-Q_{2}=3000-1314.4=1685.6 \mathrm{VAR}\]
    \[C=\frac{Q_{C}}{\omega V_{\mathrm{rms}}^{2}}=\frac{1685.6}{2 \pi \times 60 \times 120^{2}}=310.5 \mu \mathrm{F}\]
    The reactive power due to the capacitor is