Natural Response of Parallel RLC Circuits

Demonstrative Video

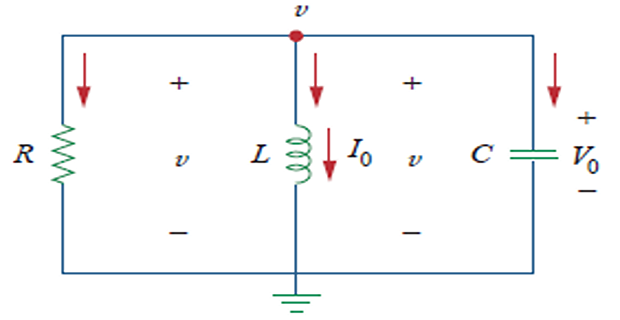
Parallel RLC Circuits

Parallel RLC Circuit - Natural Response

\[\begin{aligned} i(0)& =I_{0}=\frac{1}{L} \int_{\infty}^{0} v(t) d t \\ v(0)& =V_{0} \end{aligned}\]
  • \[\begin{aligned} & \frac{v}{R}+\frac{1}{L} \int_{-\infty}^{t} v d t+C \frac{d v}{d t}=0 \\ & \frac{d^{2} v}{d t^{2}}+\frac{1}{R C} \frac{d v}{d t}+\frac{1}{L C} v=0~\Leftarrow \text{On derivating} \\ & s^2+\dfrac{1}{RC}s+\dfrac{1}{LC} = 0~\Leftarrow \left(s \leftarrow d/dt, ~s^2 \leftarrow d^2/dt\right) \end{aligned}\]
    Applying KCL at top node:
  • \[\begin{aligned} &s_{1,2}=-\frac{1}{2 R C} \pm \sqrt{\left(\frac{1}{2 R C}\right)^{2}-\frac{1}{L C}} \\ \Rightarrow ~&s_{1,2}=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}} \\ &\alpha=\frac{1}{2 R C}, \quad \omega_{0}=\frac{1}{\sqrt{L C}} \end{aligned}\]
    Roots of

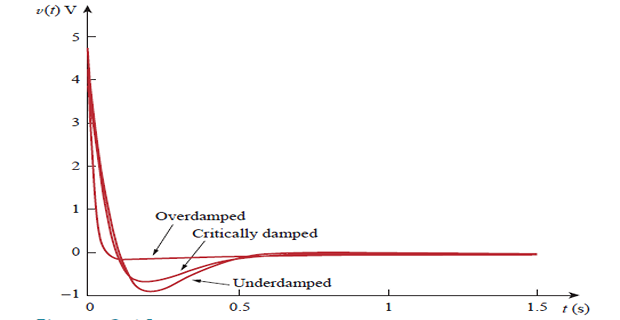
Response Cases

  1. Overdamped Case \(\left(\alpha>\omega_{0}\right)\) when \(L>4 R^{2} C\)

    • The roots of the characteristic equation are real and negative

    • \[\boxed{v(t)=A_{1} e^{s_{1} t}+A_{2} e^{s_{2} t}}\]
      The response is

  2. Critically Damped Case \(\left(\alpha=\omega_{0}\right)\) when \(L=4 R^{2} C\)

    • The roots are real and equal

    • \[\boxed{v(t)=\left(A_{1}+A_{2} t\right) e^{-\alpha t}}\]
      Response:

  3. Underdamped Case \(\left(\alpha<\omega_{0}\right)\) when \(L<4 R^{2} C\)

    • \[s_{1,2}=-\alpha \pm j \omega_{d} \quad \left( \omega_{d}=\sqrt{\omega_{0}^{2}-\alpha^{2}}\right)\]
      Roots are complex and may be expressed as
    • \[\boxed{v(t)=e^{-\alpha t}\left(A_{1} \cos \omega_{d} t+A_{2} \sin \omega_{d} t\right)}\]
      Response

    • \(A_1\) and \(A_2\) are found from initial conditions \(v(0)\) and \(dv(0)/dt\)

Solved Problem

Find \(v(t)\) for \(t>0\), given \(v(0)=5\) V, \(i(0)=0\), \(L=1\) H, and \(C=10\) mF. Consider:

  • \(R=1.923~\Omega\)

  • \(R=5~\Omega\)

  • \(R=6.25~\Omega\)

image

  • CASE-1 \(R=1.923 \Omega\)

\[\begin{aligned} \alpha&=\frac{1}{2 R C}=\frac{1}{2 \times 1.923 \times 10 \times 10^{-3}}=26 \\ \omega_{0}&=\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{1 \times 10 \times 10^{-3}}}=10\\ \Rightarrow~&\alpha>\omega_{0}~\text{over damped}\\ s_{1,2}&=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}}=-2,-50\\ v(t)&=A_{1} e^{-2 t}+A_{2} e^{-50 t}\\ v(0) &=5=A_{1}+A_{2} \\ \frac{d v(0)}{d t}=-\frac{v(0)+R i(0)}{R C} &=-\frac{5+0}{1.923 \times 10 \times 10^{-3}}=-260\\ \frac{d v}{d t}&=-2 A_{1} e^{-2 t}-50 A_{2} e^{-50 t}\\ -260&=-2 A_{1}-50 A_{2} \Leftarrow t=0\\ A_{1}&=-0.2083 \quad A_{2}=5.208\\ v(t)&=-0.2083 e^{-2 t}+5.208 e^{-50 t} \end{aligned}\]

  • CASE-2 \(R=5 \Omega\)

\[\begin{aligned} \alpha&=\frac{1}{2 R C}=\frac{1}{2 \times 5 \times 10 \times 10^{-3}}=10\\ \omega_{0}&=10~ \text{remains the same}\\ \alpha&=\omega_{0}=10 \Rightarrow \text{critically damped}\\ s_{1}&=s_{2}=-10\\ v(t)&=\left(A_{1}+A_{2} t\right) e^{-10 t} \\ v(0)&=5=A_{1} \\ \frac{d v(0)}{d t}&=-\frac{v(0)+R i(0)}{R C}=-\frac{5+0}{5 \times 10 \times 10^{-3}}=-100 \\ \frac{d v}{d t}&=\left(-10 A_{1}-10 A_{2} t+A_{2}\right) e^{-10 t} \\ -100&=-10 A_{1}+A_{2} \\ A_{1}&=5 \text { and } A_{2}=-50 \\ v(t)&=(5-50 t) e^{-10 t} \mathrm{~V} \end{aligned}\]

  • CASE-3 \(R=6.25 \Omega\)

\[\begin{aligned} \alpha&=\frac{1}{2 R C}=\frac{1}{2 \times 6.25 \times 10 \times 10^{-3}}=8\\ \omega_{0}&=10~\Rightarrow \text{ remains the same}\\ \alpha&<\omega_{0}~\Rightarrow \text{ under damped}\\ s_{1,2}&=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}}=-8 \pm j 6\\ v(t)&=\left(A_{1} \cos 6 t+A_{2} \sin 6 t\right) e^{-8 t}\\ v(0) &=5=A_{1} \\ \frac{d v(0)}{d t}&=-\frac{v(0)+R i(0)}{R C} =-\frac{5+0}{6.25 \times 10 \times 10^{-3}}=-80\\ \frac{d v}{d t}&=\left(-8 A_{1} \cos 6 t-8 A_{2} \sin 6 t-6 A_{1} \sin 6 t+6 A_{2} \cos 6 t\right) e^{-8 t}\\ -80&=-8 A_{1}+6 A_{2} \Rightarrow t=0 \\ A_{1}&=5~ \text{and}~ A_{2}=-6.667\\ v(t)&=(5 \cos 6 t-6.667 \sin 6 t) e^{-8 t}\\ \end{aligned}\]
image