Demonstrative Video
Superposition Theorem
Determine \(I_0\) using
superposition theorem?

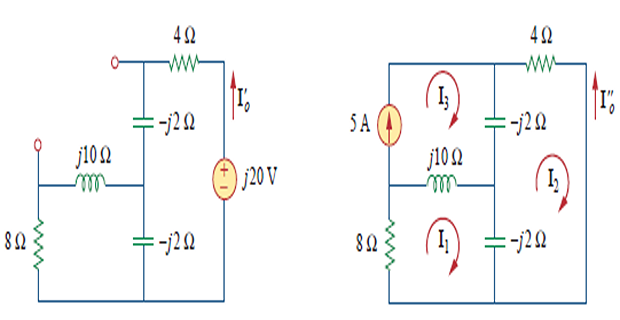
\[\begin{aligned}
\mathbf{Z} &=\frac{-j 2(8+j 10)}{-2 j+8+j 10}=0.25-j
2.25 \\
\mathbf{I}_{o}^{\prime} &=\frac{j 20}{4-j
2+\mathbf{Z}}=\frac{j 20}{4.25-j 4.25} \\
&=-2.353+j 2.353
\end{aligned}\]
\[\mathbf{I}_{o}=\mathbf{I}_{o}^{\prime}+\mathbf{I}_{o}^{\prime
\prime}=-5+j 3.529=6.12 \angle 144.78^{\circ} \mathrm{A}\]
Source Transformation
Calculate \(V_x\) using source
transformation?
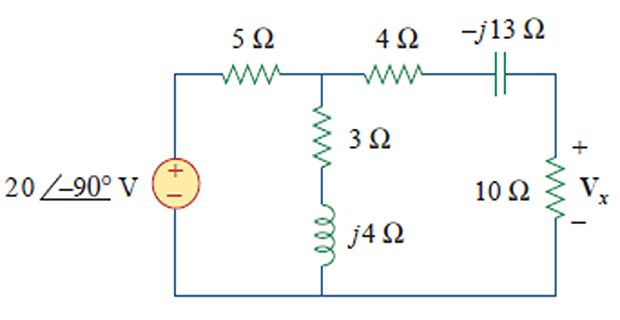
\[\begin{aligned}
I_s & = \dfrac{20\angle 90^{\circ}}{5} \\
&= -j4~\mathrm{A}
\end{aligned}\]
\[\begin{aligned}
Z_1 & = \dfrac{5(3+j4)}{8+j4} = 2.5+j1.25~\Omega\\
V_s & = I_sZ_1 = -j4(2.5+j1.25)\\
& = 5-j10~\mathrm{V}
\end{aligned}\]
\[\mathbf{V}_{x}=\frac{10}{10+2.5+j 1.25+4-j
13}(5-j 10)=5.519 \angle-28^{\circ} \mathrm{V}\]
By Voltage division:
Thevenin’s Theorem
Problem-1
Obtain the Thevenin equivalent at terminals a-b of the circuit.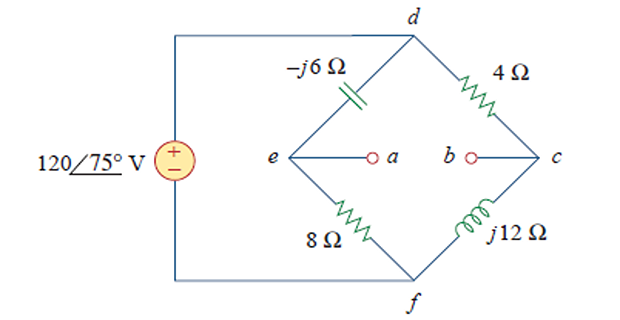
\[\begin{aligned}
&\mathbf{Z}_{1}=-j 6 \| 8=\frac{-j 6 \times 8}{8-j
6}=2.88-j 3.84 \Omega \\
&\mathbf{Z}_{2}=4 \| j 12=\frac{j 12 \times 4}{4+j
12}=3.6+j 1.2 \Omega \\
&\mathbf{Z}_{\mathrm{Th}}=\mathbf{Z}_{1}+\mathbf{Z}_{2}=6.48-j
2.64 \Omega
\end{aligned}\]
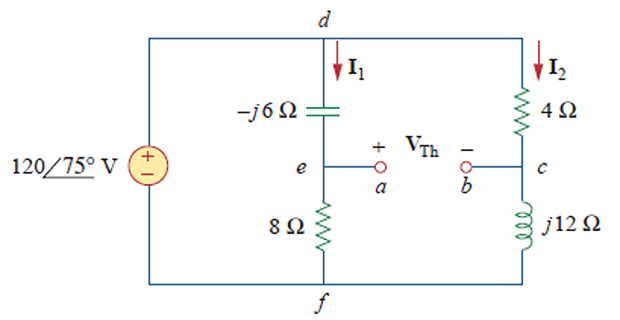
\[\begin{aligned}
& \mathbf{I}_{1}=\frac{120 \angle 75^{\circ}}{8-j 6}
\mathrm{~A}, \qquad \mathbf{I}_{2}=\frac{120 \angle 75^{\circ}}{4+j 12}
\mathrm{~A} \\
& \mathbf{V}_{\mathrm{Th}}-4 \mathbf{I}_{2}+(-j 6)
\mathbf{I}_{1}=0 \\
\Rightarrow & \mathbf{V}_{\mathrm{Th}}=4 \mathbf{I}_{2}+j 6
\mathbf{I}_{1}\\
& = \dfrac{480\angle
75^{\circ}}{4+j12}+\dfrac{720\angle{(75^{\circ}+90^{\circ})}}{8-j6}\\
& = 37.95 \angle 220.31^{\circ}
\end{aligned}\]
Problem-2
Find the Thevenin equivalent of the circuit.
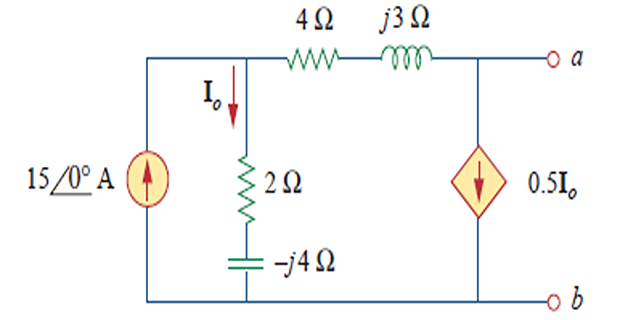

\[15=\mathbf{I}_{o}+0.5 \mathbf{I}_{o} \quad
\Rightarrow \quad \mathbf{I}_{o}=10 \mathrm{~A}\]
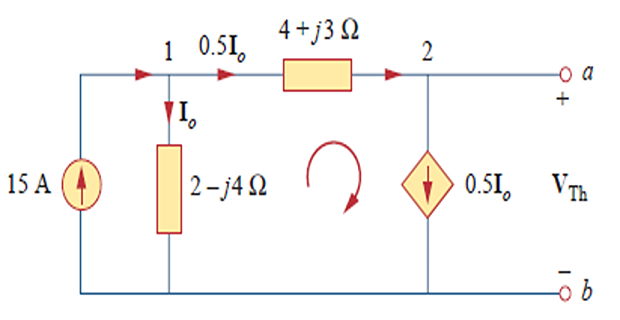
\[\begin{aligned}
& -\mathbf{I}_{o}(2-j 4)+0.5 \mathbf{I}_{o}(4+j
3)+\mathbf{V}_{\mathrm{Th}}=0 \\
& \mathbf{V}_{\mathrm{Th}}=10(2-j 4)-5(4+j 3)=-j 55\\
& \mathbf{V}_{\mathrm{Th}}=55 \angle-90^{\circ} \mathrm{V}
\end{aligned}\]
at node 1 , we apply To find
\[\begin{aligned}
&3=\mathbf{I}_{o}+0.5 \mathbf{I}_{o} \quad \Rightarrow \quad
\mathbf{I}_{o}=2 \mathrm{~A} \\
&\mathbf{V}_{s}=\mathbf{I}_{o}(4+j 3+2-j 4)=2(6-j) \\
&\mathbf{Z}_{\mathrm{Th}}=\frac{\mathbf{V}_{s}}{\mathbf{I}_{s}}=\frac{2(6-j)}{3}=4-j
0.6667 \Omega
\end{aligned}\]
Norton’s Theorem
Obtain current \(I_o\) using
Norton’s.
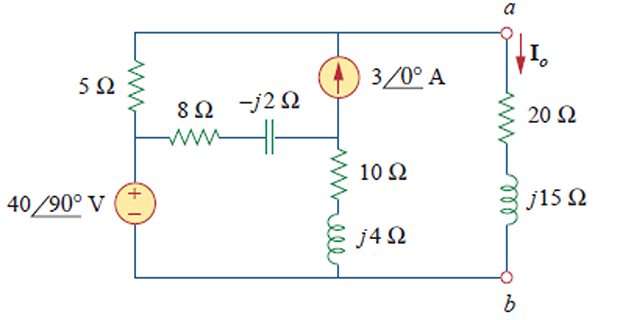
\[Z_N = 5~\Omega\]
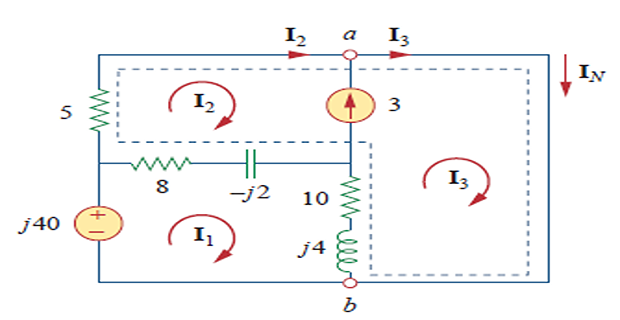
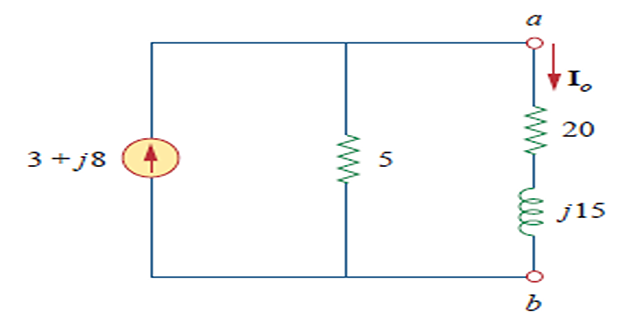
\[\begin{aligned}
-j 40+(18+j 2) \mathbf{I}_{1}-(8-j 2) \mathbf{I}_{2}-(10+j 4)
\mathbf{I}_{3} &=0 \\
(13-j 2) \mathbf{I}_{2}+(10+j 4) \mathbf{I}_{3}-(18+j 2)
\mathbf{I}_{1} &=0 \\
\mathbf{I}_{3} &=\mathbf{I}_{2}+3
\end{aligned}\]
\[\begin{aligned}
\mathbf{I}_{2} &=j 8 \qquad
\mathbf{I}_{3} =3+j 8 \\
\mathbf{I}_{N} &=\mathbf{I}_{3}=(3+j 8) \mathrm{A} \\
\mathbf{I}_{o} &=\frac{5}{5+20+j 15} \mathbf{I}_{N} \\
&=\frac{3+j 8}{5+j 3}=1.465 \angle 38.48^{\circ} \mathrm{A}
\end{aligned}\]
On solving: