Laplace Transform: Solving ODEs

Demonstrative Video

Introduction

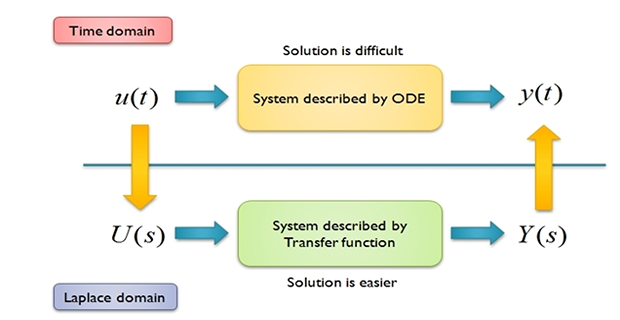
  • RLC analysis: Differential Equation (Time-domain) and Phasors (Frequency domain)

  • Laplace Transform : Differential Equation \(\Rightarrow\) Algebraic Equation

  • \[\mbox{Time-domain } \mathrel{\mathop{\rightleftarrows}^{\mathrm{{\color{red}{\textbf{Laplace}}}}}_{\mathrm{{\color{brown}{\textbf{Inverse-Laplace}}}}}} \mbox{Frequency-domain}\]
    Conversion Process

  • Advantages of Laplace-Transform:

    • can be applied to a wider variety of inputs than phasor analysis

    • provides an easy way to solve circuit problems involving initial conditions, since it work with algebraic equations instead of DE

    • capable of providing one single operation, the total response of the circuit comprising both the natural and forced responses.

image

Definition of the Laplace Transform

  • Laplace transform is an integral transformation of \(f (t )\) from the time domain into the complex frequency domain, giving \(F (s)\).

  • \[\boxed{\mathcal{L}[f(t)]=F(s)=\int_{0^{-}}^{\infty} f(t) e^{-s t} d t} \quad s=\sigma+j \omega ~~ \text{ complex variable}\]
    Mathematical definition

  • Argument \(st\) of \(e\) \(\Rightarrow\) dimensionless \(\Rightarrow\) unit of \(s\) is frequency or \(\mathrm{s}^{-1}\)

  • Lower limit \(0^{-1}\) to include origin and capture any discontinuity in \(f(t)\) at \(t=0\)

  • Definite integral \(\Rightarrow\) result independent of time \(\Rightarrow\) only involve \(s\)

  • One sided (or Unilateral)LT: Ignore for \(t < 0\) \(\Rightarrow\) \(f(t)u(t);~t \geq 0\)

  • \[F(s)=\int_{-\infty}^{\infty} f(t) e^{-s t} d t\]
    ) LT: Two-sided (or

  • One-sided LT will be adequate for circuit analysis

  • A \(f(t)\) may not have the Laplace transform

  • To have a LT of \(f(t)\) the integral must converge to finite value

  • \[\int_{0^{-}}^{\infty} e^{-\sigma t}|f(t)| d t<\infty \quad \text{for}~ \sigma = \sigma_c\]
    , integral converges when for some Since
  • \[\mathrm{Re}(s) = \sigma > \sigma_c \Rightarrow |F(s)| < \infty\]
    Region of convergence:
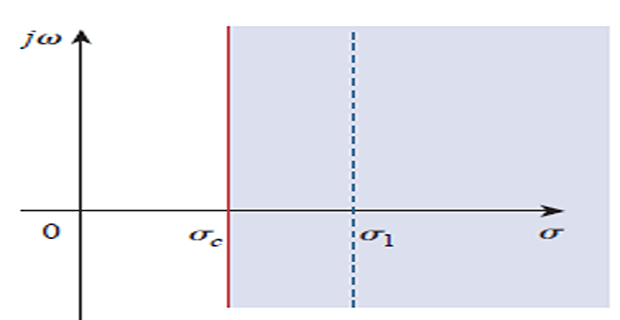
image

  • \(F(s)\) is undefined outside the region of convergence

  • \[\mathcal{L}^{-1}[F(s)]=f(t)=\frac{1}{2 \pi j} \int_{\sigma_{1}-j \omega}^{\sigma_{1}+j \omega} F(s) e^{s t} d s\]
    Inverse Laplace-transform:

Problem

\[\begin{aligned} \mathcal{L}[u(t)] &=\int_{0^{-}}^{\infty} 1 e^{-s t} d t=-\left.\frac{1}{s} e^{-s t}\right|_{0} ^{\infty}=-\frac{1}{s}(0)+\frac{1}{s}(1)=\frac{1}{s} \\ \mathcal{L}\left[e^{-a t} u(t)\right] &=\int_{0^{-}}^{\infty} e^{-a t} e^{-s t} d t=-\left.\frac{1}{s+a} e^{-(s+a) t}\right|_{0} ^{\infty}=\frac{1}{s+a} \\ \mathcal{L}[\delta(t)] &=\int_{0^{-}}^{\infty} \delta(t) e^{-s t} d t=e^{-0}=1 \\ \mathcal{L}[\sin \omega t] &=\int_{0}^{\infty}(\sin \omega t) e^{-s t} d t=\int_{0}^{\infty}\left(\frac{e^{j \omega t}-e^{-j \omega t}}{2 j}\right) e^{-s t} d t \\ &=\frac{1}{2 j} \int_{0}^{\infty}\left(e^{-(s-j \omega) t}-e^{-(s+j \omega) t}\right) d t \\ &=\frac{1}{2 j}\left(\frac{1}{s-j \omega}-\frac{1}{s+j \omega}\right)=\frac{\omega}{s^{2}+\omega^{2}} \end{aligned}\]
Determine the Laplace transform of the given functions?

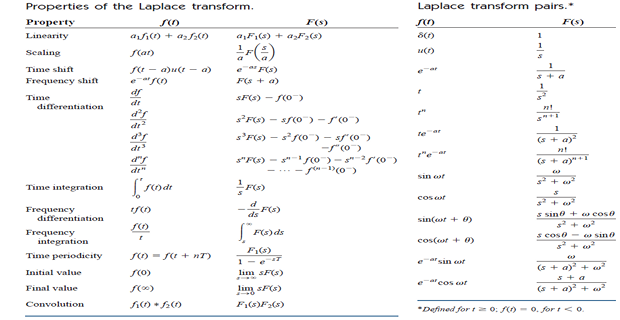
Properties of the Laplace Transform

  • \[ \mathcal{L}\left[a_{1} f_{1}(t)+a_{2} f_{2}(t)\right]=a_{1} F_{1}(s)+a_{2} F_{2}(s) \]
    Linearity
  • \[\mathcal{L}[f(a t)]=\frac{1}{a} F\left(\frac{s}{a}\right)\]
    Scaling
  • \[\mathcal{L}[f(t-a) u(t-a)]=e^{-a s} F(s)\]
    Time Shift
  • \[\mathcal{L}\left[e^{-a t} f(t) u(t)\right]=F(s+a)\]
    Frequency Shift
  • \[ \begin{aligned} \mathcal{L}\left[\frac{d^{n} f}{d t^{n}}\right]=& s^{n} F(s)-s^{n-1} f\left(0^{-}\right) \\ &-s^{n-2} f^{\prime}\left(0^{-}\right)-\cdots-s^{0} f^{(n-1)}\left(0^{-}\right) \end{aligned} \]
    Time Differentiation
  • \[\mathcal{L}\left[\int_{0}^{t} f(t) d t\right]=\frac{1}{s} F(s)\]
    Time Integration
  • \[\begin{aligned} &f(0)=\lim _{s \rightarrow \infty} s F(s) \\ &f(\infty)=\lim _{s \rightarrow 0} s F(s) \end{aligned}\]
    Initial and Final values
image

Problems


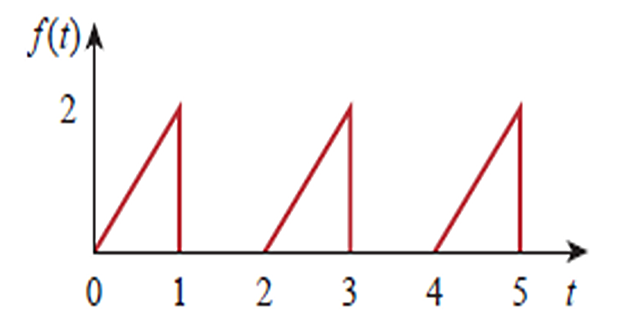
Problem-1

Find the Laplace transform of \(f(t)\) ?

\[\begin{aligned} f(t) &=\delta(t)+2 u(t)-3 e^{-2 t} u(t) \\ F(s) &=\mathcal{L}[\delta(t)]+2 \mathcal{L}[u(t)]-\\ & \qquad 3 \mathcal{L}\left[e^{-2 t} u(t)\right] \\ &=1+2 \frac{1}{s}-3 \frac{1}{s+2}\\ &=\frac{s^{2}+s+4}{s(s+2)} \end{aligned}\]
Using frequency differentiation

Problem-2

\[g(t)=10[u(t-2)-u(t-3)]\]
\[\begin{aligned} f_{1}(t) &=2 t[u(t)-u(t-1)] \qquad (T=2)\\ &=2 t u(t)-2 t u(t-1) \\ &=2 t u(t)-2(t-1+1) u(t-1) \\ &=2 t u(t)-2(t-1) u(t-1)\\ & \qquad -2 u(t-1)\\ F_{1}(s)&=\frac{2}{s^{2}}-2 \frac{e^{-s}}{s^{2}}-\frac{2}{s} e^{-s}\\ & =\frac{2}{s^{2}}\left(1-e^{-s}-s e^{-s}\right)\\ F(s)&=\frac{F_{1}(s)}{1-e^{-T s}}\\ &=\frac{2}{s^{2}\left(1-e^{-2 s}\right)}\left(1-e^{-s}-s e^{-s}\right) \end{aligned}\]
image
\[\begin{aligned} G(s) &=10\left(\frac{e^{-2 s}}{s}-\frac{e^{-3 s}}{s}\right)\\ &=\frac{10}{s}\left(e^{-2 s}-e^{-3 s}\right) \end{aligned}\]
? Find the Laplace transform of graphical
\[\begin{aligned} &\text { Find the initial and final values of the function whose Laplace transform is }\\ &H(s)=\frac{20}{(s+3)\left(s^{2}+8 s+25\right)}\\ &h(0)=\lim _{s \rightarrow \infty} s H(s)=\lim _{s \rightarrow \infty} \frac{20 s}{(s+3)\left(s^{2}+8 s+25\right)}\\ &=\lim _{s \rightarrow \infty} \frac{20 / s^{2}}{(1+3 / s)\left(1+8 / s+25 / s^{2}\right)}=\frac{0}{(1+0)(1+0+0)}=0\\ &h(\infty)=\lim _{s \rightarrow 0} s H(s)=\lim _{s \rightarrow 0} \frac{20 s}{(s+3)\left(s^{2}+8 s+25\right)}\\ &=\frac{0}{(0+3)(0+0+25)}=0 \end{aligned}\]