Fundamentals of Inductors

Demonstrative Video

Inductors

  • An inductor is a passive element designed to store energy in its magnetic field.

  • Inductors find numerous applications in electronic and power systems.

  • They are used in power supplies, transformers, radios, TVs, radars, and electric motors.

  • Any conductor of electric current has inductive properties and may be regarded as an inductor.

  • But in order to enhance the inductive effect, a practical inductor is usually formed into a cylindrical coil with many turns of conducting wire.

  • An inductor is usually constructed by coiling a wire around some type of form (core).

  • Current flowing through the coil creates a magnetic field or flux that links the coil and core.

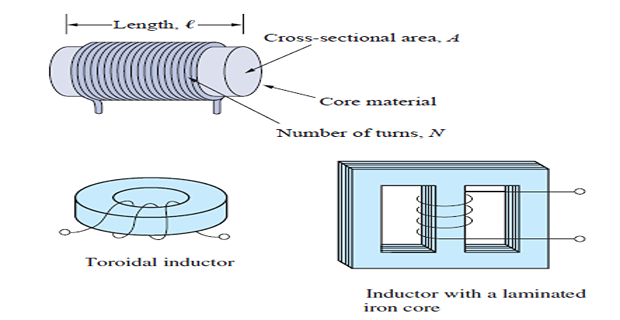
image

  • The inductance of an inductor depends on its physical dimension and construction.

  • Formulas for calculating the inductance of inductors of different shapes are derived from electromagnetic theory and can be found in standard electrical engineering handbooks.

  • \[L=\frac{N^{2} \mu A}{\ell}\]
    \(\mu\)\(A\)\(\ell\)\(N\)For example, for the inductor, (solenoid)

  • We can see from Eq. that inductance can be increased by increasing the number of turns of coil, using material with higher permeability as the core, increasing the cross-sectional area, or reducing the length of the coil.

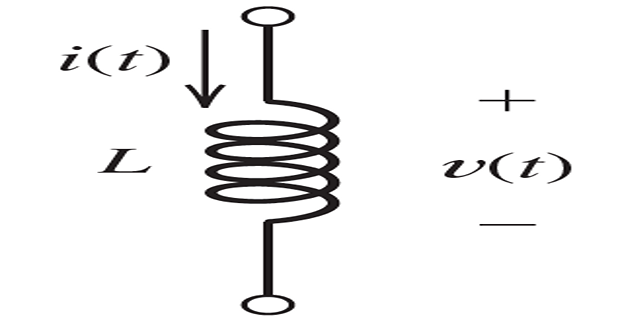
Principle

  • When \(i(t)\) changes in value, the resulting \(\Phi\) changes.

  • According to Faraday’s law of electromagnetic induction, time-varying magnetic flux linking a coil induces voltage across the coil.

  • For an ideal \(L\), the voltage is proportional to the time rate of change of the current.

  • The polarity of the voltage is such as to oppose the change in current.

  • The constant of proportionality is called inductance (\(L\)).

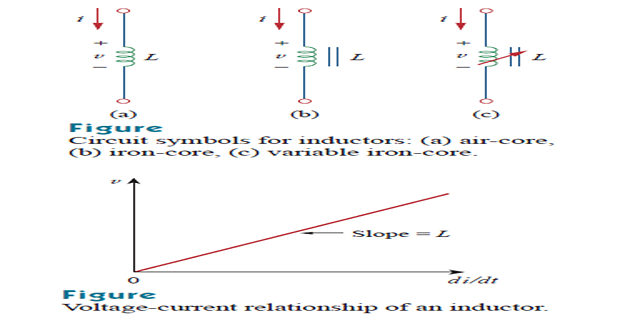
  • \[v(t) = L\cdot \dfrac{di}{dt}\]
    The voltage and current are related by:

  • Unit henries (H), which are equivalent to volt seconds per ampere.

image

  • Typically, inductances ranges from \(\mu\)H to mH

image

Fluid-Flow Analogy

  • The fluid-flow analogy for inductance is the inertia of the fluid flowing through a frictionless pipe of constant diameter.

  • The pressure differential between the ends of the pipe is analogous to voltage, and the flow rate or velocity is analogous to current.

  • Thus, the acceleration of the fluid is analogous to rate of change of current.

  • A pressure differential exists between the ends of the pipe only when the flow rate is increasing or decreasing.

  • One place where the inertia of flowing fluid is encountered is when a valve closes suddenly, cutting off the flow.

Current in Terms of Voltage

  • Suppose that we know the initial current \(i(t_0)\) and the voltage \(v(t)\) across an inductance.

  • Furthermore, suppose that we need to compute the current for \(t > t_0\)

\[\begin{aligned} v(t) &=L \frac{d i}{d t} \\ d i &=\frac{1}{L} v(t) d t \\ \int_{i\left(t_{0}\right)}^{i(t)} d i &=\frac{1}{L} \int_{t_{0}}^{t} v(t) d t \\ i(t) &=\frac{1}{L} \int_{t_{0}}^{t} v(t) d t+i\left(t_{0}\right) \end{aligned}\]

  • as long as \(v(t)\) is finite, \(i(t)\) can change only by an incremental amount in a time increment.

  • Thus, \(i(t)\) must be continuous with no instantaneous jumps in value (i.e., discontinuities).

Stored Energy

\[\begin{aligned} p(t) &=v(t) i(t) \\ p(t) &=L i(t) \frac{d i}{d t} \\ w(t) &=\int_{t_{0}}^{t} p(t) d t \\ w(t) &=\int_{t_{0}}^{t} L i \frac{d i}{d t} d t \\ w(t) &=\int_{0}^{i(t)} L i d i \\ w(t) &=\frac{1}{2} L i^{2}(t) \end{aligned}\]

  • This represents energy stored in the inductance that is returned to the circuit if the current changes back to zero.

Inductances In Series and Parallel

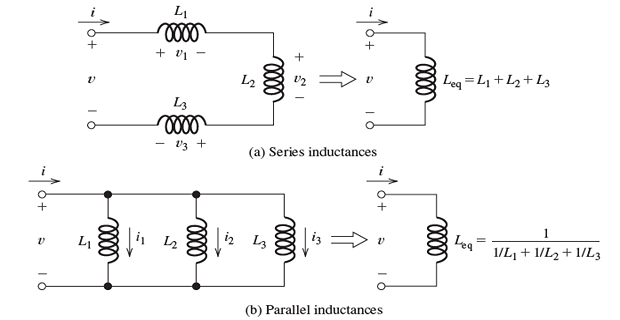
image

  • Notice that inductances are combined in exactly the same way as are resistances.

Parasitic Effects for Real Inductors

  • Real inductors have parasitic effects in addition to the desired inductance

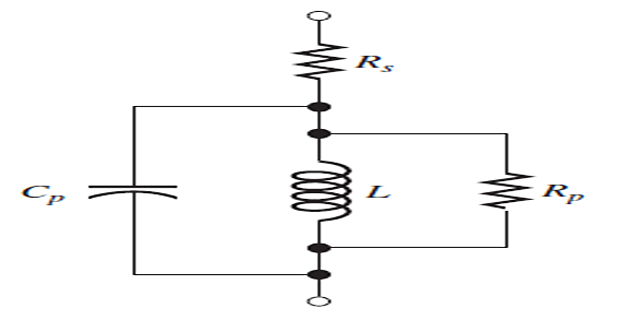
image

  • The series resistance \(R_s\) is caused by the resistivity of the material composing the wire.

  • The parallel capacitance is associated with the electric field in the dielectric (insulation) between the coils of wire. It is called inter-winding capacitance.

  • The parallel resistance \(R_p\) represents core loss due, in part, to eddy currents in the core

Important properties of an inductor

  • \[\text{An inductor acts like a short circuit to dc}\]
    the voltage across an inductor is zero when the current is constant.

  • The current through an inductor cannot change instantaneously

  • Like the ideal capacitor, the ideal inductor does not dissipate energy. The energy stored in it can be retrieved at a later time. The inductor takes power from the circuit when storing energy and delivers power to the circuit when returning previously stored energy.

  • A practical, non-ideal inductor has parasitic effect causing losses

image