Frequency Response and Transfer Functions

Demonstrative Video

Introduction

  • In sinusoidal circuit analysis, we learned to find voltages and currents in a circuit with a constant frequency source.

  • Keeping the amplitude of the sinusoidal source remain constant and vary the frequency, we obtain the circuit’s frequency response

  • Frequency response: complete description of the sinusoidal steady-state behaviour of a circuit as a function of frequency.

  • Many applications, such as communications & control systems.

  • Electric filters block out or eliminate signals with unwanted frequencies and pass signals of the desired frequencies.

  • Filters : radio, TV, and telephone systems to separate one broadcast frequency from another.

Transfer Function Representation

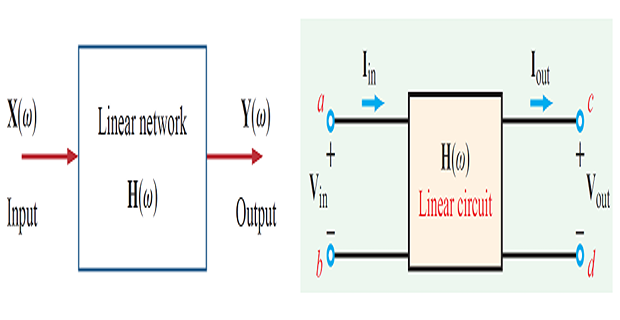
image
  • \[\begin{gathered} \mathbf{H}(\omega)=M(\omega) e^{j \phi(\omega)} \\ M(\omega)=|\mathbf{H}(\omega)| \quad \text { and } \quad \phi(\omega)=\tan ^{-1}\left\{\frac{\mathfrak{Im}[\mathbf{H}(\omega)]}{\mathfrak{Re}[\mathbf{H}(\omega)]}\right\} \end{gathered}\]
    Complex quantity

  • Magnitude and Phase plots w.r.t frequency

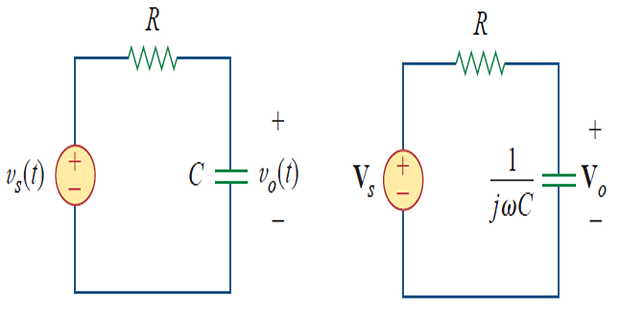
Frequency Response from TF

Obtain the TF \(V_o/V_s\) and its frequency response if \(v_s = V_m \cos\omega t\)

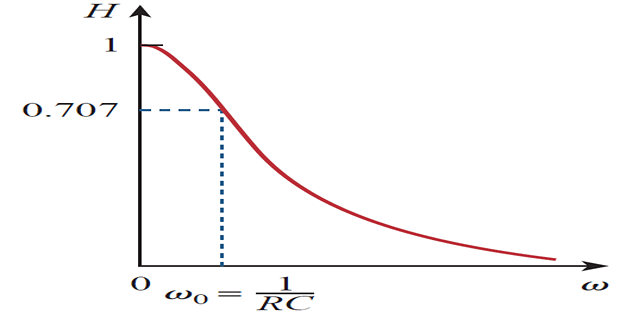
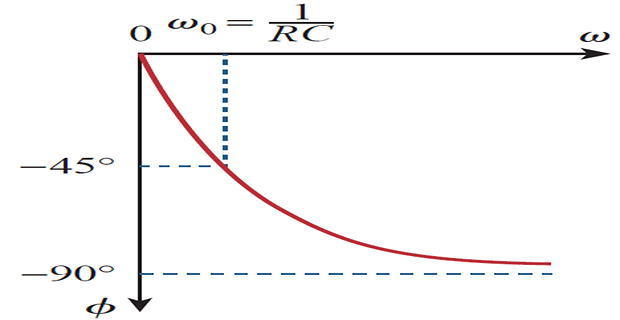
image

\[\begin{aligned} &\mathbf{H}(\omega)=\frac{\mathbf{V}_{o}}{\mathbf{V}_{s}}=\frac{1 / j \omega C}{R+1 / j \omega C}=\frac{1}{1+j \omega R C} \\ &H=\frac{1}{\sqrt{1+\left(\omega / \omega_{0}\right)^{2}}}, \quad \phi=-\tan ^{-1} \frac{\omega}{\omega_{0}}, \quad \omega_{0}=1 / R C . \end{aligned}\]
\[\begin{aligned} H&=\frac{1}{\sqrt{1+\left(\omega / \omega_{0}\right)^{2}}} \\ \phi & =-\tan ^{-1} \frac{\omega}{\omega_{0}} \end{aligned}\]
\(\omega/\omega_0\) \(\mathbf{H}\) \(\mathbf{\phi}\) \(\omega/\omega_0\) \(\mathbf{H}\) \(\mathbf{\phi}\)
0 1 0 10 0.1 -84\(^\circ\)
1 0.71 -45\(^\circ\) 20 0.05 -87\(^\circ\)
2 0.45 -63\(^\circ\) 100 0.01 -89\(^\circ\)
3 0.32 -72\(^\circ\) \(\infty\) 0 -90\(^\circ\)
image
image

The Decibel Scale

  • In communications systems, gain is measured in bels.

  • \[\begin{aligned} G & = \text{Number of bels} = \log_{10}\dfrac{P_2}{P_1} \end{aligned}\]
    The bel is used to measure the ratio of two levels of power or power gain

  • The decibel (dB) provides us with a unit of less magnitude. It is \(1/10\) of a bel and is given by

    \[\begin{aligned} &\boxed{G_{\mathrm{dB}} = 10 \log_{10}\dfrac{P_2}{P_1}} \end{aligned}\]

  • Logarithms are greatly used because the reciprocal of a quantity is simply negative the logarithm of that quantity

\[\begin{aligned} G_{\mathrm{dB}} &=10 \log _{10} \frac{P_{2}}{P_{1}}=10 \log _{10} \frac{V_{2}^{2} / R_{2}}{V_{1}^{2} / R_{1}} \\ &=10 \log _{10}\left(\frac{V_{2}}{V_{1}}\right)^{2}+10 \log _{10} \frac{R_{1}}{R_{2}} \\ G_{\mathrm{dB}} &=20 \log _{10} \frac{V_{2}}{V_{1}}-10 \log _{10} \frac{R_{2}}{R_{1}} \end{aligned}\]
\[\begin{aligned} \text{if}~R_1 & = R_2 \\ &\boxed{G_{\mathrm{dB}} =20 \log _{10} \frac{V_{2}}{V_{1}}} \\ \text{Alternatively}~P_1 & = I_1^2R_1 \quad P_2 = I_2^2R_2 \\ &\boxed{G_{\mathrm{dB}} =20 \log _{10} \frac{I_{2}}{I_{1}}} \end{aligned}\]
\[\boxed{G_{\mathrm{dB}} = 10 \log_{10}\dfrac{P_2}{P_1}} \quad \boxed{G_{\mathrm{dB}} =20 \log _{10} \frac{V_{2}}{V_{1}}} \quad \boxed{G_{\mathrm{dB}} =20 \log _{10} \frac{I_{2}}{I_{1}}}\]

  • \(10 \log_{10}\) is used for power while \(20 \log_{10}\) for voltage or current, because the square relationship exist (\(P = V^2/R = I^2R\)).

  • dB value is the logarithmic measurement of the ratio of one variable to another of the same type. Therefore, applies to TF.

  • Only voltage and current magnitudes are considered, negative signs and angles will be handled independently.

Bode Plots

  • Obtaining frequency response from the TF is a difficult task.

  • Systematic way of obtaining the frequency response is to use Bode plots.

  • Inconvenient to use a linear scale for the frequency axis as the range is very wide.

  • Semilogarithmic plots: the magnitude (dB) is plotted against the logarithm of the frequency; on a separate plot, the phase in degrees is plotted against the logarithm of the frequency

  • Bode plots are semilog plots of the magnitude (in decibels) and phase (in degrees) of a transfer function versus frequency.

  • Bode plots are easier to construct and contains all information as that of non logarithmic plots.