Convolution Integral: Understanding System Response

Demonstrative Video

The Convolution Integral

  • Convolution (means folding) is a tool for viewing and characterizing physical systems.

  • \[\begin{aligned} y(t)& =\int_{-\infty}^{\infty} x(\lambda) h(t-\lambda) d \lambda \quad \Rightarrow y(t)=x(t) * h(t) \\ \lambda & \rightarrow \text{dummy variable} \quad \text{asterisk} \rightarrow \text{convolution} \end{aligned}\]
    \(h(t)\)\(x(t)\)\(y(t)\)Convolution integral:
  • \[\begin{aligned} &y(t)=x(t) * h(t)=h(t) * x(t) \\ &y(t)=\int_{-\infty}^{\infty} x(\lambda) h(t-\lambda) d \lambda=\int_{-\infty}^{\infty} h(\lambda) x(t-\lambda) d \lambda \end{aligned}\]
    The convolution process is commutative:

  • The order in which the two functions are convolved is immaterial

  • The convolution of two signals consists of time-reversing one of the signals, shifting it, and multiplying it point by point with the second signal, and integrating the product.

  • Simplified case:

    • \[\begin{aligned} &y(t)=\int_{-\infty}^{\infty} x(\lambda) h(t-\lambda) d \lambda=\int_{0}^{\infty} x(\lambda) h(t-\lambda) d \lambda \end{aligned}\]
      \(t<0\)\(x(t)=0\)Case-1:
    • \[\begin{aligned} &\boxed{y(t)=h(t) * x(t)=\int_{0}^{t} x(\lambda) h(t-\lambda) d \lambda} \end{aligned}\]
      \(\lambda > t\)\((t-\lambda) < 0\)\(h(t-\lambda)=0\)\(\Rightarrow\)\(t<0\)causal system\(h(t)=0\)Case-2:

Properties of the Convolution Integral

  1. \(x(t) * h(t)=h(t) * x(t)\) (Commutative)

  2. \(f(t) *[x(t)+y(t)]=f(t) * x(t)+f(t) * y(t)\) (Distributive)

  3. \(f(t) *[x(t) * y(t)]=[f(t) * x(t)] * y(t)\) (Associative)

  4. \(f(t) * \delta(t)=\int_{-\infty}^{\infty} f(\lambda) \delta(t-\lambda) d \lambda=f(t)\)

  5. \(f(t) * \delta\left(t-t_{o}\right)=f\left(t-t_{o}\right)\)

  6. \(f(t) * \delta^{\prime}(t)=\int_{-\infty}^{\infty} f(\lambda) \delta^{\prime}(t-\lambda) d \lambda=f^{\prime}(t)\)

  7. \(f(t) * u(t)=\int_{-\infty}^{\infty} f(\lambda) u(t-\lambda) d \lambda=\int_{-\infty}^{t} f(\lambda) d \lambda\)

  • \[\begin{aligned} &f(t)=f_{1}(t) * f_{2}(t)=\int_{0}^{t} f_{1}(\lambda) f_{2}(t-\lambda) d \lambda \\ &F(s)=\boxed{\mathcal{L}\left[f_{1}(t) * f_{2}(t)\right]=F_{1}(s) F_{2}(s)} \end{aligned}\]
    Link between Laplace transform and convolution integral:

  • This indicates that convolution in the time domain is equivalent to multiplication in the s-domain

  • Convolution in some cases is better in time-domain only

    • Product \(F_1(s) \cdot F_2(s)\) is very complicated finding inverse is difficult

    • \(f_1(t)\) and \(f_2(t)\) available in experimental data and there is no explicit Laplace transform

  • The process of convolving two signals in the time domain is better appreciated from a graphical point of view

  • Steps: graphical procedure for evaluating the convolution integral

    1. Folding: Take the mirror image of \(h(\lambda)\) about the ordinate axis to obtain \(h(-\lambda)\).

    2. Displacement: Shift or delay \(h(-\lambda)\) by \(t\) to obtain \(h(t-\lambda)\).

    3. Multiplication: Find the product of \(h(t-\lambda)\) and \(x(\lambda)\).

    4. Integration: For a given time \(t\), calculate the area under the product \(h(t-\lambda) x(\lambda)\) for \(0<\lambda<t\) to get \(y(t)\) at \(t\).

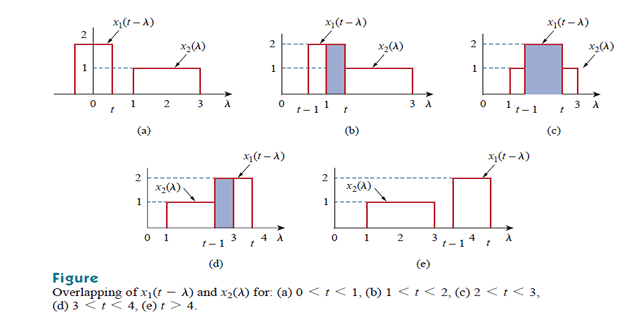
Problem

Find the convolution of the two signals ?

Solution:

  • Four steps to get \(y(t) = x_1(t)*x_2(t)\)

  • Fold \(x_1(t)\) and shift it by \(t\)

  • For different \(t\), multiply the two functions and integrate to determine overlapping area

image

image

image
\[\begin{aligned} &y(t)=x_{1}(t) * x_{2}(t)=0, \quad 0<t<1 \\ &y(t)=\int_{1}^{t}(2)(1) d \lambda=\left.2 \lambda\right|_{1} ^{t}=2(t-1), \quad 1<t<2 \\ &y(t)=\int_{t-1}^{t}(2)(1) d \lambda=\left.2 \lambda\right|_{t-1} ^{t}=2, \quad 2<t<3 \\ &y(t)=\int_{t-1}^{3}(2)(1) d \lambda=\left.2 \lambda\right|_{t-1} ^{3}=2(3-t+1)=8-2 t, \quad 3<t<4 \\ &y(t)=0, \quad t>4 \end{aligned}\]
\[y(t)= \begin{cases}0, & 0 \leq t \leq 1 \\ 2 t-2, & 1 \leq t \leq 2 \\ 2, & 2 \leq t \leq 3 \\ 8-2 t, & 3 \leq t \leq 4 \\ 0, & t \geq 4\end{cases}\]

Problem

\[\begin{aligned} I_{o} &=\frac{1}{s+1} I_{s} \\ H(s) &=\frac{I_{o}}{I_{s}}=\frac{1}{s+1} \\ h(t) &=e^{-t} u(t) \\ i_{s}(t) &=u(t)-u(t-2) \\ I_{o}(s) &=H(s) I_{s}(s) \\ i_{o}(t) &=h(t) * i_{s}(t)=\int_{0}^{t} i_{s}(\lambda) h(t-\lambda) d \lambda \\ &=\int_{0}^{t}[u(\lambda)-u(\lambda-2)] e^{-(t-\lambda)} d \lambda \end{aligned}\]
image

image
of the RL circuit due to the given excitation source ? Use the convolution integral to find the response
\[\begin{aligned} &i_{o}^{\prime}(t)=\int_{0}^{t}(1) e^{-(t-\lambda)} d \lambda=e^{-t} \int_{0}^{t}(1) e^{\lambda} d \lambda\\ &=e^{-t}\left(e^{t}-1\right)=1-e^{-t}, \quad 0<t<2\\ &i_{o}^{\prime \prime}(t)=\int_{2}^{t}(1) e^{-(t-\lambda)} d \lambda=e^{-t} \int_{2}^{t} e^{\lambda} d \lambda\\ &=e^{-t}\left(e^{t}-e^{2}\right)=1-e^{2} e^{-t}, \quad t>2\\ &i_{o}(t)=i_{o}^{\prime}(t)-i_{o}^{\prime \prime}(t)\\ &=\left(1-e^{-t}\right)[u(t-2)-u(t)]-\left(1-e^{2} e^{-t}\right) u(t-2)\\ &= \begin{cases}1-e^{-t} \mathrm{~A}, & 0<t<2 \\ \left(e^{2}-1\right) e^{-t} \mathrm{~A}, & t>2\end{cases} \end{aligned}\]

image

image