Complex Power Analysis in AC Circuits

Demonstrative Video

Complex Power

  • Complex power is important in power analysis because it contains all the information pertaining to the power absorbed by a given load.

image
\[\begin{aligned} & \mathbf{V}=V_m\angle \theta_v \qquad \mathbf{I}=I_m\angle \theta_i\\ &\mathrm{S}=\frac{1}{2} \mathrm{VI}^{*}\qquad \mathrm{S}=\mathrm{V}_{\mathrm{rms}} \mathbf{I}_{\mathrm{rm}}^{*}\\ &\mathbf{V}_{\text {rms }}=\frac{\mathbf{V}}{\sqrt{2}}=V_{\text {rms }} \angle \theta_{v} \qquad \mathbf{I}_{\text {rms }}=\frac{\mathbf{I}}{\sqrt{2}}=I_{\text {rms }} / \theta_{i}\\ &\mathrm{S}=V_{\mathrm{rms}} I_{\mathrm{rms}} \angle{ \theta_{v}-\theta_{i}}\quad =V_{\mathrm{rms}} I_{\mathrm{rms}} \cos \left(\theta_{v}-\theta_{i}\right)+j V_{\mathrm{rms}} I_{\mathrm{rms}} \sin \left(\theta_{v}-\theta_{i}\right)\\ &\mathbf{Z}=\frac{\mathbf{V}}{\mathbf{I}}=\frac{\mathbf{V}_{\mathrm{rms}}}{\mathbf{I}_{\mathrm{rms}}}=\frac{V_{\mathrm{rms}}}{I_{\mathrm{rms}}} \angle {\theta_{v}-\theta_{i}}\\ &\boxed{\mathbf{S}=I_{\mathrm{rms}}^{2} \mathbf{Z}=\frac{V_{\mathrm{rms}}^{2}}{\mathbf{Z}^{*}}=\mathbf{V}_{\mathrm{rms}} \mathbf{I}_{\mathrm{rms}}^{*}} \end{aligned}\]
\[\begin{aligned} \color{magenta}{\text{Complex-power}}~& \mathbf{S}=I_{\mathrm{rms}}^{2}(R+j X)=P+j Q\\ \color{brown}{\text{Real-power}}~&P=\operatorname{Re}(\mathrm{S})=I_{\mathrm{rm}_{\mathrm{S}}}^{2} R\\ \color{teal}{\text{Reactive-power}}~&Q=\operatorname{Im}(\mathrm{S})=I_{\mathrm{rms}}^{2} X\\ & P = V_{rms}I_{rms}\cos(\theta_v-\theta_i) \quad Q = V_{rms}I_{rms}\sin(\theta_v-\theta_i) \end{aligned}\]

  • The real power P is the average power in watts delivered to a load; it is the only useful power or actual power dissipated by the load.

  • The reactive power Q is a measure of the energy exchange between the source and the reactive part of the load. The unit of Q is the volt-ampere reactive (VAR).

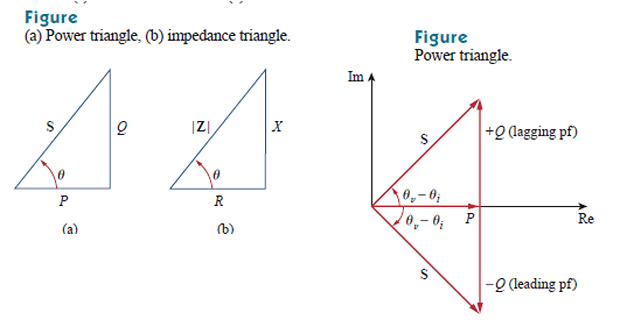
  1. \(Q=0\) for resistive loads (unity pf)

  2. \(Q<0\) for capacitive loads (leading pf)

  3. \(Q>0\) for inductive loads (lagging pf)

image

Revision

\[\begin{aligned} \text { Complex Power }&=\mathbf{S}=P+j Q=\mathbf{V}_{\mathrm{rms}}\left(\mathbf{I}_{\mathrm{rms}}\right)^{*} = \mathbf{V}_{\mathrm{rms}} \mathbf{I}_{\mathrm{rms}} \angle \theta_{v}-\theta_{i} \\ \text { Apparent Power }&=S=|\mathbf{S}|=\mathbf{V}_{\mathrm{rms}} \mathbf{I}_{\mathrm{rms}}=\sqrt{P^{2}+Q^{2}} \\ \text { Real Power }&=P=\operatorname{Re}(\mathbf{S})=S \cos \left(\theta_{v}-\theta_{i}\right) \\ \text { Reactive Power }&=Q=\operatorname{Im}(\mathbf{S})=S \sin \left(\theta_{v}-\theta_{i}\right) \\ \text { Power Factor }&=\frac{P}{S}=\cos \left(\theta_{v}-\theta_{i}\right) \end{aligned}\]

Complex Power Problems

Problem-1

  • The voltage across a load is \(v(t)=60 \cos \left(\omega t-10^{\circ}\right) \mathrm{V}\) and the current through the element in the direction of the voltage drop is \(i(t)=\) \(1.5 \cos \left(\omega t+50^{\circ}\right) \mathrm{A}\). Find: (a) the complex and apparent powers, (b) the real and reactive powers, and (c) the power factor and the load impedance.

  • \[\mathbf{V}_{\mathrm{rms}}=\frac{60}{\sqrt{2}} \angle -10^{\circ}, \quad \mathbf{I}_{\mathrm{rms}}=\frac{1.5}{\sqrt{2}} \angle +50^{\circ}\]
    Solution: For the rms values of the voltage and current, we write
  • \[\mathrm{S}=\mathbf{V}_{\mathrm{rms}} \mathbf{I}_{\mathrm{rms}}^{*}=\left(\frac{60}{\sqrt{2}} \angle -10^{\circ}\right)\left(\frac{1.5}{\sqrt{2}} \angle -50^{\circ}\right)=45 \angle-60^{\circ} \mathrm{VA}\]
    The complex power is
  • \[S=|\mathbf{S}|=45 \mathrm{VA}\]
    The apparent power is
  • \[\mathrm{S}=45 \angle -60^{\circ}=45\left[\cos \left(-60^{\circ}\right)+j \sin \left(-60^{\circ}\right)\right]=22.5-j 38.97\]
    complex power in rectangular form as
  • \[P=22.5 \mathrm{~W} \qquad Q=-38.97 \mathrm{VAR}\]
    , the real and reactive power are Since
  • \[\mathrm{pf}=\cos \left(-60^{\circ}\right)=0.5 \text { (leading) }\]
    The power factor is
  • \[\mathbf{Z}=\frac{\mathbf{V}}{\mathbf{I}}=\frac{60 \angle-10^{\circ}}{1.5 \angle+50^{\circ}}=40 \angle-60^{\circ} \Omega\]
    The load impedance is

Problem-2

  • A load \(\mathbf{Z}\) draws \(12 \mathrm{kVA}\) at a power factor of \(0.856\) lagging from a 120 -V rms sinusoidal source. Calculate: (a) the average and reactive powers delivered to the load, (b) the peak current, and (c) the load impedance.

  • Solution: Given \(\mathrm{pf}=\cos \theta=0.856\), \(\Rightarrow\) power angle \(\theta=\cos ^{-1} 0.856=31.13^{\circ}\).

  • \[P=S \cos \theta=12,000 \times 0.856=10.272 \mathrm{~kW}\]
    \[Q=S \sin \theta=12,000 \times 0.517=6.204 \mathrm{kVA}\]
    , then the average or real power is Apparent power is
  • \[\mathrm{S}=P+j Q=10.272+j 6.204 \mathrm{kVA}\]
    is lagging, the complex power is Since the
  • \[\mathbf{I}_{\mathrm{rms}}^{*}=\frac{\mathbf{S}}{\mathbf{V}_{\mathrm{rms}}}=\frac{10,272+j 6204}{120 \angle 0^{\circ}}=85.6+j 51.7 \mathrm{~A}=100 \angle 31.13^{\circ} \mathrm{A}\]
    , we obtain From
  • \[I_{m}=\sqrt{2} I_{\mathrm{rms}}=\sqrt{2}(100)=141.4 \mathrm{~A}\]
    and the peak current is Thus
  • \[\mathbf{Z}=\frac{\mathbf{V}_{\mathrm{rms}}}{\mathbf{I}_{\mathrm{rms}}}=\frac{120 \angle 0^{\circ}}{100 \angle -31.13^{\circ}}=1.2 / 31.13^{\circ} \Omega\]
    The load impedance