Fundamentals of Capacitors

Demonstrative Video

Introduction

  • Previously, we studied circuits composed of resistances and sources.

  • Now, we discuss two additional circuit elements: inductors and capacitors.

  • Resistors convert electrical energy into heat

  • Inductors and capacitors are energy-storage elements.

  • They can store energy and later return it to the circuit.

  • They do not generate energy—only the energy that has been put into these elements can be extracted.

  • Thus, like resistors, they are said to be passive elements.

  • EMFT is the basic approach to the study of the effects of electrical charge.

  • Circuit theory is a simplification of field theory that is much easier to apply.

  • Capacitance is the circuit property that accounts for energy stored in electric fields.

  • Inductance accounts for energy stored in magnetic fields.

  • The voltage across an ideal inductor is proportional to the time derivative of the current.

  • The voltage across an ideal capacitor is proportional to the time integral of the current.

  • Mutual inductance is the circuit property that accounts for magnetic fields that are mutual to several inductors.

  • Mutual inductance forms the basis for transformers, which are critical to the transmission of electrical power over long distances.

  • Several types of transducers are based on inductance and capacitance

Capacitance

  • A capacitor is a passive element designed to store energy in its electric field.

  • Capacitors are constructed by separating two sheets of conductor, which is usually metallic, by a thin layer of insulating material.

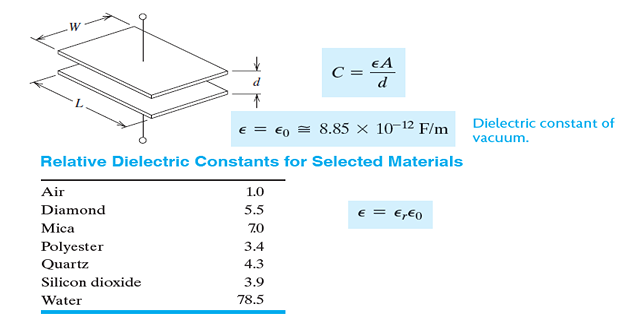
  • In a parallel-plate capacitor (\(C=\epsilon A/d\)), the sheets are flat and parallel.

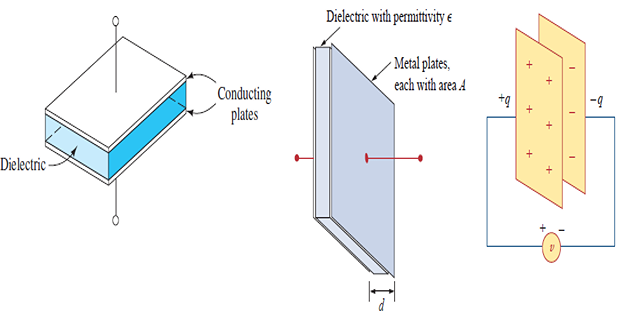
    image

  • The insulating material between the plates, called a dielectric, can be air, polyester, polypropylene, mica, or a variety of other materials.

  • Capacitors are used extensively in electronics, communications, computers, and power systems.

Capacitance of the Parallel-Plate Capacitor

image

Capacitance & Fluid-Flow Analogy

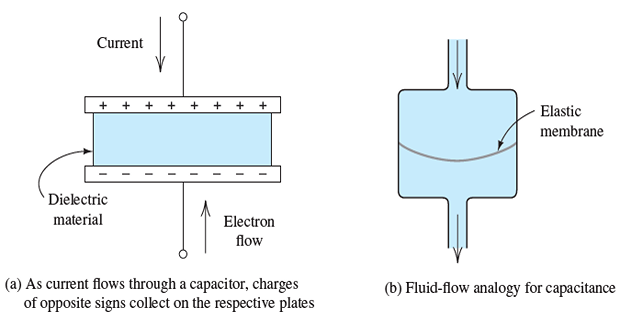
image

  • Suppose current in the capacitor flows downward.

  • Current consists of moving electrons, and conventional current flowing downward represents electrons actually moving upward.

  • As electrons move upward, they collect on the lower plate of the capacitor.

  • Thus, the lower plate accumulates a net negative charge that produces an electric field in the dielectric.

  • This electric field forces electrons to leave the upper plate at the same rate that they accumulate on the lower plate.

  • Therefore, current appears to flow through the capacitor.

  • As the charge builds up, voltage appears across the capacitor.

  • We say that the charge accumulated on one plate is stored in the capacitor.

  • However, the total charge on both plates is always zero, because positive charge on one plate is balanced by negative charge of equal magnitude on the other plate.

  • In terms of the fluid-flow analogy, a capacitor represents a reservoir with an elastic membrane separating the inlet and outlet.

  • As the fluid flows into the inlet, the membrane is stretched, creating a force (analogous to capacitor voltage) that opposes further flow.

  • The displaced fluid volume starting from the un-stretched membrane position is analogous to the charge stored on one plate of the capacitor.

Commercial available capacitors

image

Important properties of a capacitor

  • \[\text{A capacitor is an open circuit to dc.}\]
    When the voltage across a capacitor is not changing with time (i.e., dc voltage), the current through the capacitor is zero. Thus,

  • However, if a battery (dc voltage) is connected across a capacitor, the capacitor charges.

  • The voltage on a capacitor cannot change abruptly.

  • The ideal capacitor does not dissipate energy. It takes power from the circuit when storing energy in its field and returns previously stored energy when delivering power to the circuit.

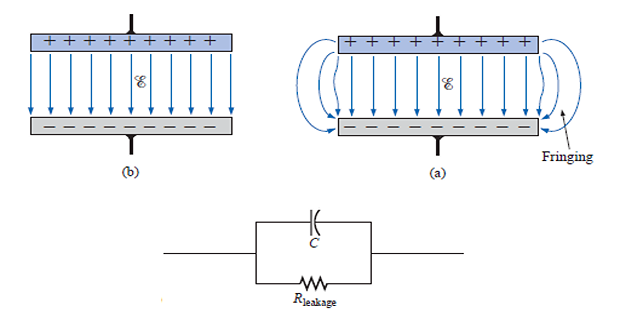
  • A real, non-ideal capacitor has a parallel-model leakage resistance. The leakage resistance may be as high as 100 M\(\Omega\) and can be neglected in practical applications.

image

Stored Charge & Current in Terms of Voltage

  • \[\boxed{q = C\cdot v}\]
    is proportional to the voltage between the plates: In an ideal capacitor, the stored charge

  • The constant of proportionality is the capacitance \(C\), which has units of farads (F), equivalent to coulombs per volt.

  • Recall that current is the time rate of flow of charge

    \[i = \dfrac{dq}{dt} = \dfrac{d(Cv)}{dt} = C\dfrac{dv}{dt}\]

  • Capacitance is not a function of time.

  • \(v\uparrow \Rightarrow i\) flows through \(C\) and \(q\) accumulates on each plate.

  • If \(v\) remains constant, \(q\) is constant and \(i=0\).

  • Thus, a \(C\) appears to be an open-circuit for a steady dc voltage.

Voltage in Terms of Current

  • Computation of \(q\) and \(v\) for known \(i\) through \(C\)

\[\begin{aligned} &i(t)=C \frac{d v(t)}{d t} \\ &q(t)=\int_{t_{0}}^{t} i(t) d t+q\left(t_{0}\right) \\ &v(t)=\frac{1}{C} \int_{t_{0}}^{t} i(t) d t+\frac{q\left(t_{0}\right)}{C} \\ &v(t)=\frac{1}{C} \int_{t_{0}}^{t} i(t) d t+v\left(t_{0}\right) \end{aligned}\]

Stored Energy in a Capacitor

  • Suppose \(C\) that initially has \(v(t_0) = 0\).

  • Then the initial stored electrical energy is zero, and we say that the capacitor is uncharged

\[\begin{aligned} p(t) &=v(t) i(t) \\ p(t) &=C v \frac{d v}{d t} \\ w(t) &=\int_{t_{0}}^{t} p(t) d t \\ w(t) &=\int_{t_{0}}^{t} C v \frac{d v}{d t} d t w(t) =\int_{0}^{v(t)} C v d v \\ w(t) &=\frac{1}{2} C v^{2}(t) \\ w(t) &=\frac{1}{2} v(t) q(t) \\ &=\frac{q^{2}(t)}{2 C} \end{aligned}\]

Capacitances in Series and Parallel

  • Capacitances in Parallel
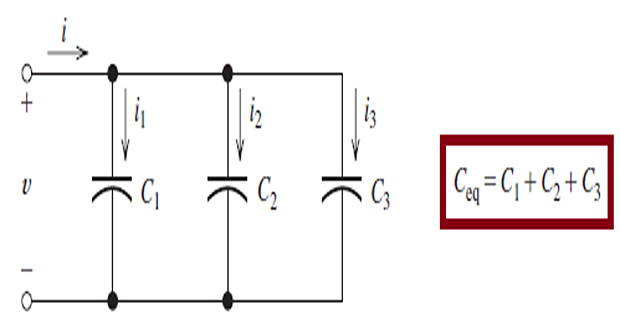
    image
\[\begin{gathered} i_{1}=C_{1} \frac{d v}{d t} \quad i_{2}=C_{2} \frac{d v}{d t} \quad i_{3}=C_{3} \frac{d v}{d t} \\ i=i_{1}+i_{2}+i_{3} \\ i=C_{1} \frac{d v}{d t}+C_{2} \frac{d v}{d t}+C_{3} \frac{d v}{d t} \\ i=\left(C_{1}+C_{2}+C_{3}\right) \frac{d v}{d t} \\ C_{\mathrm{eq}}=C_{1}+C_{2}+C_{3} \\ i=C_{\mathrm{eq}} \frac{d v}{d t} \end{gathered}\]
  • Capacitances in Series
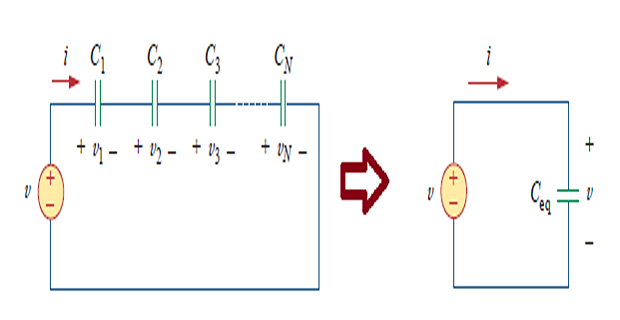
    image
  • \[v=v_{1}+v_{2}+v_{3}+\cdots+v_{N}\]
    Voltage distribution

  • But \(v_{k}=\dfrac{1}{C_{k}} \int_{t_{0}}^{t} i(t) d t+v_{k}\left(t_{0}\right) .\)

  • \[\begin{aligned} v &=\frac{1}{C_{1}} \int_{t_{0}}^{t} i(t) d t+v_{1}\left(t_{0}\right)+\frac{1}{C_{2}} \int_{t_{0}}^{t} i(t) d t+v_{2}\left(t_{0}\right)+\cdots+\\ &+\frac{1}{C_{N}} \int_{t_{0}}^{t} i(t) d t+v_{N}\left(t_{0}\right) \\ &=\left(\frac{1}{C_{1}}+\frac{1}{C_{2}}+\cdots+\frac{1}{C_{N}}\right) \int_{t_{0}}^{t} i(t) d t+v_{1}\left(t_{0}\right)+v_{2}\left(t_{0}\right)+\cdots+v_{N}\left(t_{0}\right) \\ &=\frac{1}{C_{\mathrm{eq}}} \int_{t_{0}}^{t} i(t) d t+v\left(t_{0}\right) \end{aligned}\]
    Therefore,
  • \[\frac{1}{C_{\mathrm{eq}}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\cdots+\frac{1}{C_{N}}\]
    where