Demonstrative Video
Power in a Balanced System
\[\begin{aligned}
v_{A N}& =\sqrt{2} V_{p} \cos \omega t \\
v_{B N}&=\sqrt{2} V_{p} \cos \left(\omega
t-120^{\circ}\right) \\
v_{C N}&=\sqrt{2} V_{p} \cos \left(\omega
t+120^{\circ}\right)
\end{aligned}\]
\[\begin{aligned}
p&=p_{a}+p_{b}+p_{c}=v_{A N} i_{a}+v_{B N} i_{b}+v_{C N} i_{c}
\\
&=2 V_{p} I_{p}\left[\cos \omega t \cos (\omega t-\theta)+\cos
\left(\omega t-120^{\circ}\right) \cos \left(\omega
t-\theta-120^{\circ}\right)\right.
+\\
& ~~ \qquad \left.\cos \left(\omega t+120^{\circ}\right) \cos
\left(\omega t-\theta+120^{\circ}\right)\right] \\
=&V_{p} I_{p}\left[3 \cos \theta+\cos (2 \omega t-\theta)+\cos
\left(2 \omega t-\theta-240^{\circ}\right)+\cos \left(2 \omega
t-\theta+240^{\circ}\right)\right] \\
=&V_{p} I_{p}[3 \cos \theta+\cos \alpha+\cos \alpha \cos
240^{\circ}+\sin \alpha \sin 240^{\circ}+\cos \alpha \cos 240^{\circ}\\
& \qquad \qquad -\sin \alpha \sin 240^{\circ}] \\
=&V_{p} I_{p}\left[3 \cos \theta+\cos
\alpha+2\left(-\frac{1}{2}\right) \cos \alpha\right]=\boxed{3 V_{p}
I_{p} \cos \theta}~~\boxed{\alpha = 2\omega t - \theta }
\end{aligned}\]
Note:
Important Points:
Thus the total instantaneous power in a balanced \(3-\phi\) system is constant—it does not change with time as the instantaneous power of each phase does.
This result is true whether the load is Y- or \(\Delta\)-connected.
This is one important reason for using a three-phase system to generate and distribute power.
\[\begin{aligned}
P_{p} &=V_{p} I_{p} \cos \theta \\
Q_{p} &=V_{p} I_{p} \sin \theta \\
S_{p} &=V_{p} I_{p} \\
\mathbf{S}_{p} &=P_{p}+j Q_{p}=\mathbf{V}_{p}
\mathbf{I}_{p}^{*} \\
P &=P_{a}+P_{b}+P_{c} \\
&=3 P_{p} \\
&=3 V_{p} I_{p} \cos \theta=\sqrt{3} V_{L} I_{L} \cos
\theta
\end{aligned}\]
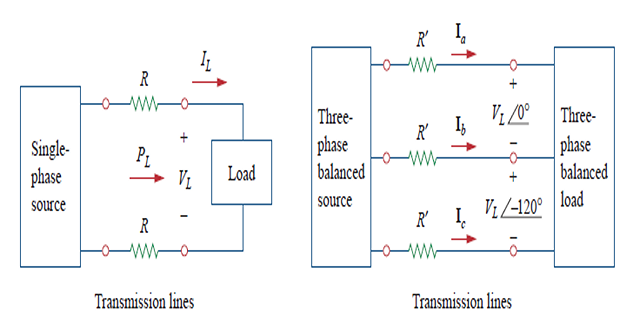
\[\begin{aligned}
P_{\text {loss }} &=2 I_{L}^{2} R=2 R
\frac{P_{L}^{2}}{V_{L}^{2}}\\
P_{\text {loss }}^{\prime}&=3\left(I_{L}^{\prime}\right)^{2}
R^{\prime}=3 R^{\prime} \frac{P_{L}^{2}}{3 V_{L}^{2}}=R^{\prime}
\frac{P_{L}^{2}}{V_{L}^{2}}\\
&\frac{P_{\text {loss }}}{P_{\text {loss
}}^{\prime}}=\frac{2 R}{R^{\prime}} \\
&R=\rho \ell / \pi r^{2} \text { and } R^{\prime}=\rho \ell
/ \pi r^{\prime 2} \\
&\frac{P_{\text {loss }}}{P_{\text {loss
}}^{\prime}}=\frac{2 r^{\prime 2}}{r^{2}}
\end{aligned}\]
system. system use 33% more material than
If the same power loss is tolerated in
both systems, then
Problem
Determine the total average power, reactive power, and complex power
at the source and at the load.
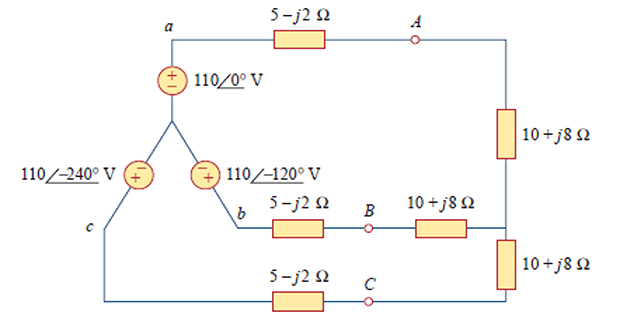

\[\begin{aligned}
\mathbf{V}_{p} &=110 \angle 0^{\circ} \mathrm{V} \\
\mathbf{I}_{p} &=6.81 \angle-21.8^{\circ} \mathrm{A} \\
\mathbf{S}_{s} &=-3 \mathbf{V}_{p} \mathbf{I}_{p}^{*}\\
&=-3\left(110 \angle 0^{\circ}\right)\left(6.81 \angle
21.8^{\circ}\right) \\
&=-2247 \angle 21.8^{\circ}\\
&=-(2087+j 834.6) \mathrm{VA} \\
\mathbf{S}_{L} &=3\left|\mathbf{I}_{p}\right|^{2}
\mathbf{Z}_{p} \\
\end{aligned}\]