Balanced Three-Phase Circuits

Demonstrative Video

Introduction

  • A single-phase ac power system consists of a generator connected through a pair of wires (a transmission line) to a load.

  • An ac generator designed to develop a single sinusoidal voltage for each rotation of the shaft (rotor) is referred to as a single-phase ac generator.

  • If the number of coils on the rotor is increased in a specified manner, the result is a polyphase ac generator, which develops more than one ac phase voltage per rotation of the rotor.

  • Three-phase system most frequently used for power transmission.

Polyphase System

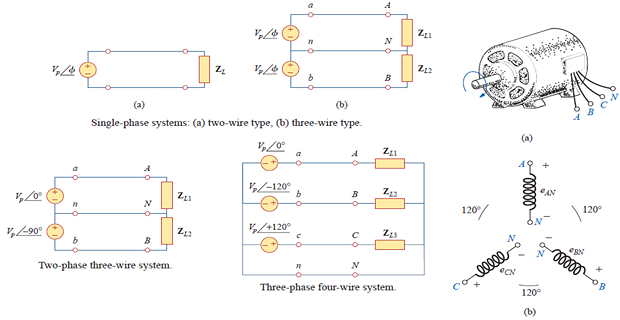
image

  • In the normal household system is a \(1-\phi\) three-wire system because the terminal voltages have the same magnitude and the same phase

  • Circuits or systems in which the ac sources operate at the same frequency but different phases are known as polyphase

Advantages of \(3-\phi\) System over \(1-\phi\) System

For same Electric power:

  • Generation (Alternator) : Power to weight ratio \(\uparrow\), size \(\downarrow\), overall cost \(\downarrow\), Weight \(\downarrow ~\Rightarrow\) transportation and installation become convenient and less space is required.

  • T & D : conductor material \(\downarrow ~\Rightarrow\) economical

  • Under UPF condition:
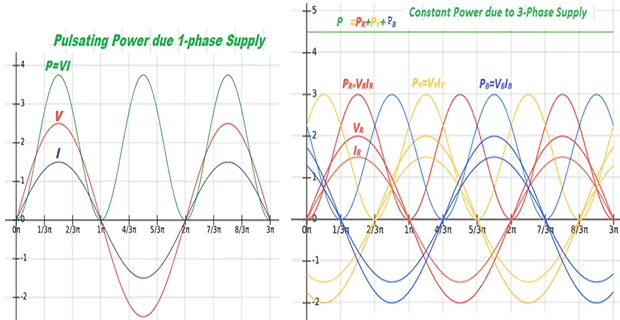
    image

  • Same condition of Power to weight ratio for 3-\(\phi\) IM (Load) and TF.

  • 3-\(\phi\) Induction Motor are self-starting but 1-\(\phi\) not so some arrangements are required which increase cost.

  • 3-phase motor is having better power factor

  • Reliability under fault condition.

  • A \(3\phi\) system can feed a \(1\phi\) load, whereas vice-versa is not possible.

Balanced Three-Phase Voltages

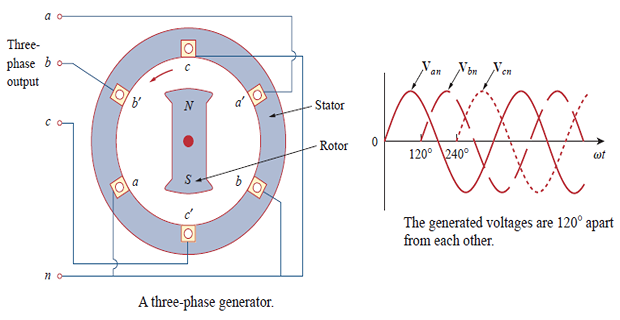
image

  • \(3-\phi\) voltages are produced by alternator having coils with terminals \(a-a^{\prime}\), \(b-b^{\prime}\), and \(c-c^{\prime}\) that are physically placed at \(120^{\circ}\) apart.

  • As the rotor rotates, its magnetic field cuts the flux from the three coils and then voltage is induced in the coils.

  • Induced voltages are equal in magnitude but out of phase by \(180^{\circ}\).

  • Balanced phase voltages are equal in magnitude and are out of phase with each other by \(120^{\circ}\)

  • A \(3\phi\) system \(\sim\) \(3 \times 1\phi\) circuits.

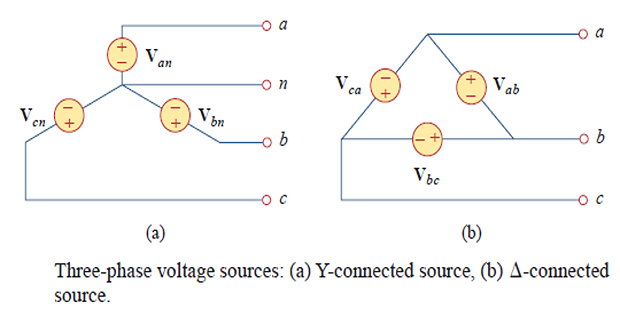
  • The voltage sources can be either Y-connected or delta-connected.

  • \(\mathbf{V_{an}}\), \(\mathbf{V_{bn}}\), \(\mathbf{V_{cn}}\) \(\Rightarrow\) Phase voltages

image
\[\begin{aligned} &\mathbf{V}_{a n}+\mathbf{V}_{b n}+\mathbf{V}_{c n}=0\\ &\left|\mathbf{V}_{a n}\right|=\left|\mathbf{V}_{b n}\right|=\left|\mathbf{V}_{c n}\right|\\ &\mathbf{V}_{a n}=V_{p} \angle 0^{\circ}\\ &\mathbf{V}_{b n}=V_{p} \angle -120^{\circ}\\ &\mathbf{V}_{c n}=V_{p} \angle-240^{\circ}=V_{p} \angle+120^{\circ} \end{aligned}\]

  • abc or positive sequence

  • produced when rotor rotates counter-clockwise

\[\begin{aligned} &\mathbf{V}_{a n}=V_{p} \angle 0^{\circ}\\ &\mathbf{V}_{c n}=V_{p} \angle -120^{\circ}\\ &\mathbf{V}_{b n}=V_{p} \angle-240^{\circ}=V_{p} \angle+120^{\circ} \end{aligned}\]

  • acb or negative sequence

  • produced when rotor rotates clockwise

\[\begin{aligned} \mathbf{V}_{a n}+\mathbf{V}_{b n}+\mathbf{V}_{c n} &=V_{p} \angle 0^{\circ}+V_{p} \angle-120^{\circ}+V_{p} \angle+120^{\circ} \\ &=V_{p}(1.0-0.5-j 0.866-0.5+j 0.866) \\ &=0 \end{aligned}\]

  • The phase sequence is the time order in which the voltages pass through their respective maximum values.

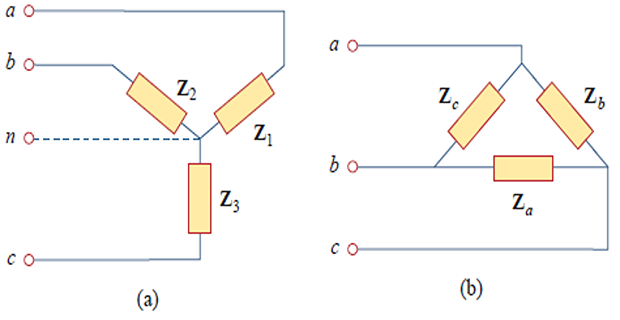
  • A balanced load is one in which the phase impedances are equal in magnitude and in phase.

  • \[\begin{aligned} &\mathbf{Z}_{1}=\mathbf{Z}_{2}=\mathbf{Z}_{3}=\mathbf{Z}_{Y} \\ &\mathbf{Z}_{a}=\mathbf{Z}_{b}=\mathbf{Z}_{c}=\mathbf{Z}_{\Delta} \\ &\mathbf{Z}_{\Delta}=3 \mathbf{Z}_{Y} \quad \text { or } \quad \mathbf{Z}_{Y}=\frac{1}{3} \mathbf{Z}_{\Delta} \end{aligned}\]
    For Balanced Loads:
image

  • Source-Load Combinations:

    • \(Y-Y\)

    • \(Y-\Delta\)

    • \(\Delta-Y\)

    • \(\Delta - \Delta\)

Problem

\[\begin{gathered} v_{a n}=200 \cos \left(\omega t+10^{\circ}\right) \\ v_{b n}=200 \cos \left(\omega t-230^{\circ}\right), \quad v_{c n}=200 \cos \left(\omega t-110^{\circ}\right) \end{gathered}\]
Solution:Determine the phase sequence of the set of voltages
\[\mathbf{V}_{a n}=200 \angle 10^{\circ} \mathrm{V}, \quad \mathbf{V}_{b n}=200 \angle-230^{\circ} \mathrm{V}, \quad \mathbf{V}_{c n}=200 \angle-110^{\circ} \mathrm{V}\]
The voltages can be expressed in phasor form as

We notice that \(\mathbf{V}_{a n}\) leads \(\mathbf{V}_{c n}\) by \(120^{\circ}\) and \(\mathbf{V}_{c n}\) in turn leads \(\mathbf{V}_{b n}\) by \(120^{\circ}\). Hence, we have an \(acb\) sequence .