Step Response of RLC Circuits

Demonstrative Video

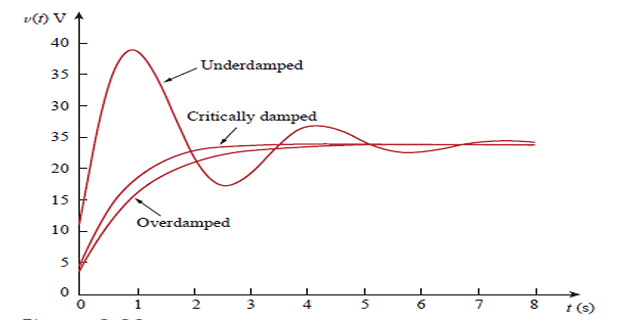
Types of Responses of Series RLC Circuits

Step Response of a Series RLC Circuit

  • \[\begin{aligned} & L \frac{d i}{d t}+R i+v=V_{s} \quad \left(i=C \frac{d v}{d t}\right)\\ \Rightarrow & \frac{d^{2} v}{d t^{2}}+\frac{R}{L} \frac{d v}{d t}+\frac{v}{L C}=\frac{V_{s}}{L C} \\ \end{aligned}\]
    Applying KVL:
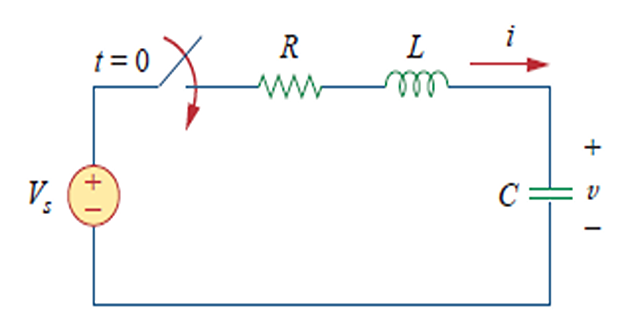
image

  • Solution: \(v(t)=v_{t}(t)+v_{s s}(t)\)

  • \[\begin{aligned} v_{t}(t)&=A_{1} e^{s_{1} t}+A_{2} e^{s_{2} t} \quad \text { (Overdamped) } \\ v_{t}(t)&=\left(A_{1}+A_{2} t\right) e^{-\alpha t} \quad \text { (Critically damped) } \\ v_{t}(t)&=\left(A_{1} \cos \omega_{d} t+A_{2} \sin \omega_{d} t\right) e^{-\alpha t} \quad \text { (Underdamped) } \end{aligned}\]
    Transient response:

  • Steady-state response \(v_{ss}(t)= v(\infty) = V_{s}\)

  • \(A_1\) and \(A_2\) are found from initial conditions \(v(0)\) and \(dv(0)/dt\)

Problem

  • Find \(v(t)\) and \(i(t)\) for \(t>0\) considering \(R=5~\Omega\), \(R=4~\Omega\),and \(R=1~\Omega\).

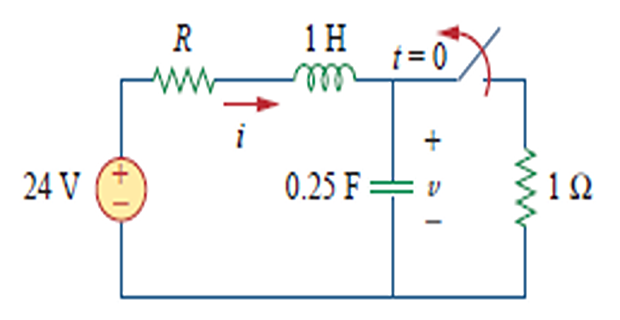
image

  • Case-I: \(R=5~\Omega\)

\[\begin{aligned} &i(0)=\frac{24}{5+1}=4 \mathrm{~A} \quad v(0)=1 i(0)=4 \mathrm{~V}\\ &\alpha=\frac{R}{2 L}=\frac{5}{2 \times 1}=2.5 \quad \omega_{0}=\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{1 \times 0.25}}=2\\ &s_{1,2}=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}}=-1,-4\\ &\alpha>\omega_{0}, \quad \Leftarrow \text {overdamped natural response. }\\ &v(t)=v_{s s}+\left(A_{1} e^{-t}+A_{2} e^{-4 t}\right) \quad \Rightarrow v(t)=24+\left(A_{1} e^{-t}+A_{2} e^{-4 t}\right)\\ &v(0)=4=24+A_{1}+A_{2}\\ &i(0)=C \frac{d v(0)}{d t}=4 \quad \Rightarrow \quad \frac{d v(0)}{d t}=\frac{4}{C}=\frac{4}{0.25}=16\\ &\frac{d v}{d t}=-A_{1} e^{-t}-4 A_{2} e^{-4 t} \Rightarrow \frac{d v(0)}{d t}=16=-A_{1}-4 A_{2}\\ &A_{1}=-64 / 3 \text { and } A_{2}=4 / 3 .\\ &\boxed{v(t)=24+\frac{4}{3}\left(-16 e^{-t}+e^{-4 t}\right) \mathrm{V}} \quad \boxed{i(t)=C \frac{d v}{d t}=\frac{4}{3}\left(4 e^{-t}-e^{-4 t}\right) \mathrm{A}} \end{aligned}\]

  • Case-II: \(R=4~\Omega\)

\[\begin{aligned} i(0)&=\frac{24}{4+1}=4.8 \mathrm{~A} \quad v(0)=1 i(0)=4.8 \mathrm{~V} \\ \alpha &=\frac{R}{2 L}=\frac{4}{2 \times 1}=2 \quad \omega_{0}=2 \text { remains the same. } \\ s_{1} &=s_{2}=-\alpha=-2 \Rightarrow \text { critically damped natural response } \\ v(t) &=v_{s s}+\left(A_{1}+A_{2} t\right) e^{-2 t} \quad \Rightarrow v(t)=24+\left(A_{1}+A_{2} t\right) e^{-2 t} \\ v(0) &=4.8=24+A_{1} \quad \Rightarrow \quad A_{1}=-19.2 \\ i(0) &=C d v(0) / d t=4.8 \quad \Rightarrow \quad \frac{d v(0)}{d t}=\frac{4.8}{C}=19.2 \\ \frac{d v}{d t} &=\left(-2 A_{1}-2 t A_{2}+A_{2}\right) e^{-2 t} \Rightarrow \frac{d v(0)}{d t}=19.2=-2 A_{1}+A_{2} \\ A_{1}&=-19.2 \text { and } A_{2}=-19.2 . \\ &\boxed{v(t)=24-19.2(1+t) e^{-2 t} \mathrm{~V} }\quad \boxed{i(t) = C\frac{d v}{d t} =(4.8+9.6 t) e^{-2 t} \mathrm{~A} } \end{aligned}\]

  • Case-III: \(R=1~\Omega\)

\[\begin{aligned} i(0)&=\frac{24}{1+1}=12 \mathrm{~A} \quad v(0)=1 i(0)=12 \mathrm{~V} \\ \alpha&=\frac{R}{2 L}=\frac{1}{2 \times 1}=0.5 \quad <\omega_{0}=2, \text { underdamped response } \\ s_{1,2}&=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}}=-0.5 \pm j 1.936 \\ v(t)&=24+\left(A_{1} \cos 1.936 t+A_{2} \sin 1.936 t\right) e^{-0.5 t} \\ v(0)&=12=24+A_{1} \quad \Rightarrow \quad A_{1}=-12 \\ i(0)&=C d v(0) / d t=12, \quad \Rightarrow \quad \frac{d v(0)}{d t}=\frac{12}{C}=48 \\ \frac{d v}{d t}=& e^{-0.5 t}\left(-1.936 A_{1} \sin 1.936 t+1.936 A_{2} \cos 1.936 t\right) \\ &-0.5 e^{-0.5 t}\left(A_{1} \cos 1.936 t+A_{2} \sin 1.936 t\right) \\ \frac{d v(0)}{d t}=& 48=\left(-0+1.936 A_{2}\right)-0.5\left(A_{1}+0\right) \quad \therefore \quad A_{1}=-12 \quad A_{2}=21.694 \end{aligned}\]
\[\begin{aligned} v(t)=& 24+(21.694 \sin 1.936 t-12 \cos 1.936 t) e^{-0.5 t} \mathrm{~V} \\ i(t)=& C \frac{d v}{d t} = \quad(3.1 \sin 1.936 t+12 \cos 1.936 t) e^{-0.5 t} \mathrm{~A} \end{aligned}\]
image

Step Response of a Parallel RLC Circuit

  • \[\begin{aligned} &\frac{v}{R}+i+C \frac{d v}{d t}=I_{s} \quad \left(v=L \frac{d i}{d t} \right) \\ \Rightarrow & \frac{d^{2} i}{d t^{2}}+\frac{1}{R C} \frac{d i}{d t}+\frac{i}{L C}=\frac{I_{s}}{L C} \end{aligned}\]
    : Applying KCL for
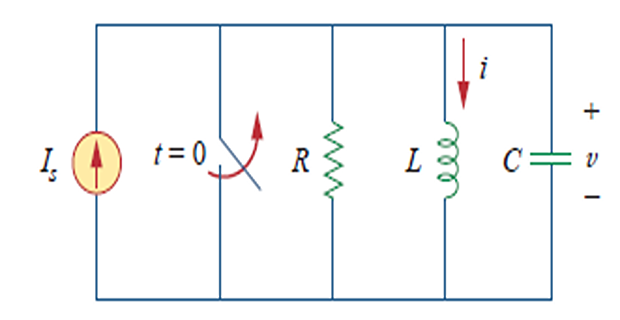
image

  • Solution: \(i(t)=i_{t}(t)+i_{s s}(t)\)

  • \[\begin{aligned} i(t)&=I_{s}+A_{1} e^{s_{1} t}+A_{2} e^{s_{2} t} \quad \text { (Overdamped) } \\ i(t)&=I_{s}+\left(A_{1}+A_{2} t\right) e^{-\alpha t} \quad \text { (Critically damped) } \\ i(t)&=I_{s}+\left(A_{1} \cos \omega_{d} t+A_{2} \sin \omega_{d} t\right) e^{-\alpha t} \quad \text { (Underdamped) } \end{aligned}\]
    Response:

  • \(A_1\) and \(A_2\) are found from initial conditions \(i(0)\) and \(di(0)/dt\)

Problem

Determine \(i(t)\) and \(i_R(t)\) for \(t>0\)

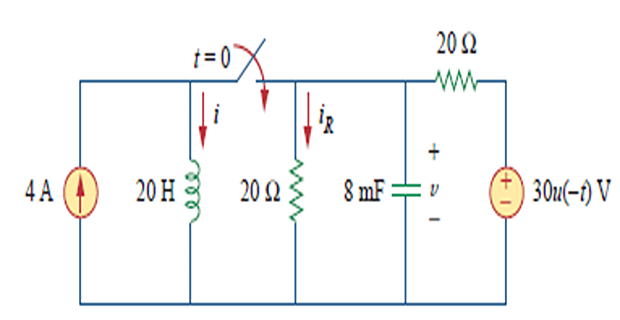
image

  • \[i(0)=4~\mathrm{A}\]
    , the switch is open For
  • \[v(0) = \dfrac{20}{20+20}\times 30 = 15~\mathrm{V}\]
    Initial capacitor voltage

  • For \(t<0\), the switch is closed and we have parallel RLC circuit with current source

  • Resistance \(R=20||20=10~\Omega\)

\[\begin{gathered} \alpha=\frac{1}{2 R C}=\frac{1}{2 \times 10 \times 8 \times 10^{-3}}=6.25 \\ \omega_{0}=\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{20 \times 8 \times 10^{-3}}}=2.5 \\ s_{1,2}=-\alpha \pm \sqrt{\alpha^{2}-\omega_{0}^{2}}=-6.25 \pm 5.7282 \\ s_{1}=-11.978, \quad s_{2}=-0.5218 \end{gathered}\]
  • \[i(t)=I_{s}+A_{1} e^{-11.978 t}+A_{2} e^{-0.5218 t}\]
    \(i(t)\)\(I_{s}=4\), we have the overdamped case. Since

  • We now use the initial conditions to determine \(A_{1}\) and \(A_{2}\).

  • \[i(0)=4=4+A_{1}+A_{2} \quad \Rightarrow \quad A_{2}=-A_{1}\]
    , At
  • \[\frac{d i}{d t}=-11.978 A_{1} e^{-11.978 t}-0.5218 A_{2} e^{-0.5218 t}\]
    , Taking the derivative of
  • \[\frac{d i(0)}{d t}=-11.978 A_{1}-0.5218 A_{2}\]
    , At
  • \[L \frac{d i(0)}{d t}=v(0)=15 \quad \Rightarrow \quad \frac{d i(0)}{d t}=\frac{15}{L}=\frac{15}{20}=0.75\]
    \[0.75=(11.978-0.5218) A_{2} \quad \Rightarrow \quad A_{2}=0.0655\]
    But

  • Thus, \(A_{1}=-0.0655\) and \(A_{2}=0.0655\).

  • \[i(t)=4+0.0655\left(e^{-0.5218 t}-e^{-11.978 t}\right) \mathrm{A}\]
    in gives the complete solution as and Inserting
  • \[i_{R}(t)=\frac{v(t)}{20}=\frac{L}{20} \frac{d i}{d t}=0.785 e^{-11.978 t}-0.0342 e^{-0.5218 t} \mathrm{~A}\]
    and , we obtain From

Second Order : Problem Solving Steps

  1. Determine initial and final values \(x(0)\) and \(d x(0) / d t\) and \(x(\infty)\)

  2. Turn off independent sources and find the transient response \(x_{t}(t)\) by applying KCL and KVL.

  3. Determine \(2^{nd}\) order D.E. and its characteristic roots.

  4. Determine response case : overdamped, critically damped, or underdamped,

  5. Obtain \(x_{t}(t)\) with two unknown constants

  6. Obtain the steady-state response as \(x_{s s}(t)=x(\infty)\) where \(x(\infty)\) is the final value of \(x\), obtained in step 1 .

  7. \[x(t)=x_{t}(t)+x_{s s}(t)\]
    The total response is

  8. Determine the constants of transient response using \(x(0)\) and \(d x(0) / d t\), determined in step 1 .