Step Response of RL Circuits

Demonstrative Video

RL Circuit with Source

Step Response of an RL Circuit

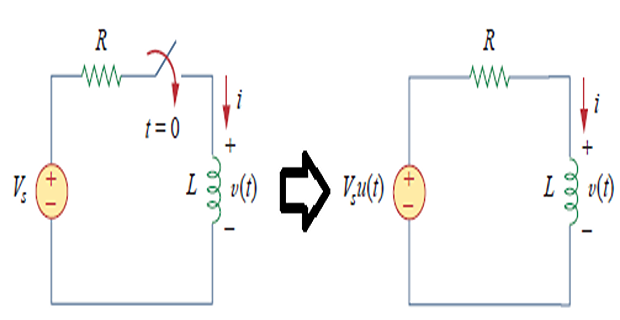
image
  • \[\begin{aligned} Ri+L\dfrac{di}{dt}&=V_s \cdot u(t)\\ Ri+L\dfrac{di}{dt}&=V_s \quad t>0 \end{aligned}\]
    Applying KVL, we get
  • \[\dfrac{Ldi}{V_s-Ri} = dt\]
    Separating variables yields
  • \[-\dfrac{L}{R}\ln(V_s-Ri)=t+A\]
    On integrating
  • \[A = -\dfrac{L}{R}\ln(V_s)\]
    At

  • Final solution

\[\begin{gathered} -\frac{L}{R}\left[\ln \left(V_{s}-R i\right)-\ln V_{s}\right]=t \\ \frac{V_{s}-R i}{V_{s}}=e^{-R t / L} \\ i=\frac{V_{s}}{R}-\frac{V_{s}}{R} e^{-R t / L} \quad t>0 \\ \boxed{i=\frac{V_{s}}{R}\left(1- e^{- t / \tau}\right) u(t)}\\ \boxed{\tau=\dfrac{L}{R}} \end{gathered}\]

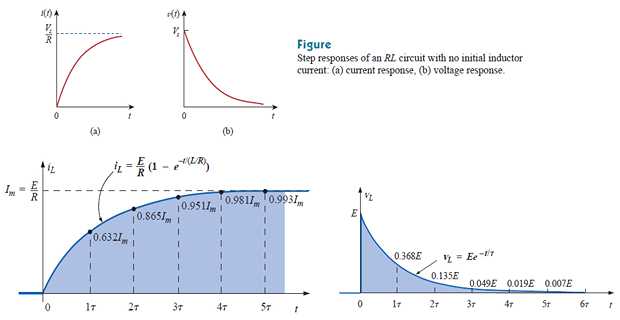
Solution for voltage

\[\begin{aligned} i(t) & =\frac{V_{s}}{R}\left(1-e^{-t / \tau}\right) u(t) \\ v(t) & =L \frac{d i}{d t}=V_{s} \frac{L}{\tau R} e^{-t / \tau}, \quad \tau=\frac{L}{R}, \quad t>0 \\ & \boxed{v(t) =V_{s} e^{-t / \tau} u(t) } \end{aligned}\]
image

Problem Solving Steps

  • \[i(t)=i(\infty)+[i(0)-i(\infty)] e^{-t / \tau}\]
    General solution:
  • \[i(t)=i(\infty)+\left[i\left(t_{0}\right)-i(\infty)\right] e^{-\left(t-t_{0}\right) / \tau}\]
    For time delay, general solution becomes

  • Steps:

    1. The initial inductor current \(i(0)\) at \(t=0\).

    2. The final inductor current \(i(\infty)\).

    3. The time constant \(\tau\).

Solved Problem

Find \(i(t)\) for \(t>0\) assuming the switch has been closed for a long time.

  • \(i(0)=i(0^-)=i(0^+)=\dfrac{10}{2}=5~\mathrm{A}\)

  • \(i(\infty) = \dfrac{10}{2+3}=2~\mathrm{A}\)

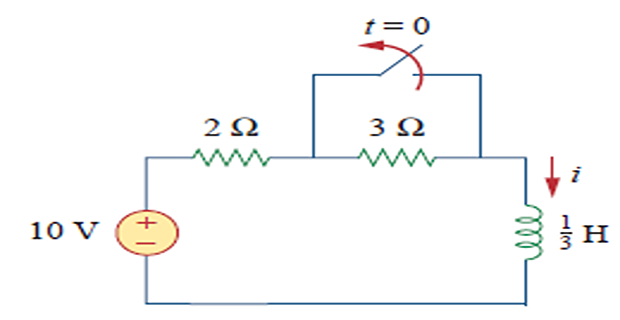
image

  • \(R_{TH} = 2+3=5~\Omega\)

  • \(\tau=\dfrac{L}{R_{Th}}=\dfrac{1}{15}~\text{sec}\)

  • \[\begin{aligned} i(t) &=i(\infty)+[i(0)-i(\infty)] e^{-t / \tau} \\ &=2+(5-2) e^{-15 t}=2+3 e^{-15 t} \mathrm{~A}, \quad t>0 \end{aligned}\]
    Current,

Revision of Formulas

RC-Circuits

  • \[\begin{aligned} &v(t)=V_{0} e^{-t / \tau} \\ &i_{R}(t)=\frac{v(t)}{R}=\frac{V_{0}}{R} e^{-t / \tau} \end{aligned}\]
    Natural Response
  • \[\begin{aligned} &v(t)=V_{s}\left(1-e^{-t / \tau}\right) u(t) \\ &i(t)=\frac{V_{s}}{R} e^{-t / \tau} u(t) \end{aligned}\]
    Forced Response
\[\boxed{\tau = RC}\]

RL-Circuits

  • \[\begin{aligned} &i(t)=I_{0} e^{-t / \tau} \\ &v_{R}(t)=i R=I_{0} R e^{-t / \tau} \end{aligned}\]
    Natural Response
  • \[\begin{aligned} &i(t)=\frac{V_{s}}{R}\left(1-e^{-t / \tau}\right) u(t) \\ &v(t)=V_{s} e^{-t / \tau} u(t) \end{aligned}\]
    Forced Response
\[\boxed{\tau = \dfrac{L}{R}}\]

  • Complete response = Natural Response + Forced Response